Extraction and evaluation of transportation network grammars for efficient planning applications

Abstract

Grammars, with their generic approach and broad application potential in many planning fields, are accepted as adaptable and efficient tools for design and planning applications, bridging design rules and technical planning requirements. This paper provides a formal introduction of grammars for effective consolidation and application, including a rule-based notation and required specification information. Two proposed grammar evaluation methods – based on technical planning knowledge and using recent computational development – foster understanding of a grammar’s effects, often missing in other definitions. Knowledge gained enables efficient grammar rule application, e.g. in burgeoning planning software. This research focuses particularly on urban network design and road intersection grammars to validate proposed grammar evaluation methods. Results are specified in the proposed grammar notation with corresponding application specifications. Results generally show that network topology and intersection type choice both depend on transport mode characteristics and flow. Specifically, medium-dense gridiron networks are car-efficient in terms of travel costs and reliability at urban densities, when combined with high road and intersection capacities. Pedestrian networks ideally have higher intersection and road densities with lower capacities than car networks. Highly meshed networks improve overall travel cost efficiencies for all transport modes at various flow levels.

1 Introduction

Transportation networks serve as backbones for economic and overall societal development and welfare, providing economic benefit through transportation of goods, persons, knowledge and information for given generalized costs (e.g. Venables 2007). For these reasons, societies have invested substantial shares of their gross domestic product in transportation infrastructure. Key advances are travel speed and capacity increases for transportation networks and a growing share of world population and economies benefiting from traveling further with lower costs. When looking at these investments, real-world transportation network topologies and shapes diverge between different networks; many different shapes and topologies have already been realized. However, a common consensus still seems to be missing on certain network design aspects, in both real-world network design and literature. In parallel, also, design methods vary between each other, and current methods are often incomplete or missing verification; and a generic planning framework is lacking for transport network planning and design.

Historically, planners and architects have proposed and designed numerous networks differing in topology, shape and metrics. In each era, transport networks were designed for specific requirements, differing considerably between cities (e.g. Jacobs 1993; Lampugnani 2010). Around the world, medieval structures contrast with baroque layouts and gridirons; these layouts also differ widely from garden cities to modernist layouts, as well as lollipop networks, based on treelike layouts with high dead-end densities. Medieval networks grew through a largely self-organized planning process, in contrast to more recent networks, constructed over shorter time periods in rather top-down planning approaches. These topologies are distinguishable by their specific design characteristics (e.g. Cardillo et al. 2006). Parcel shapes have changed considerably over time (Figure 2(d); Strano et al. 2012), and many have converged from diverse shapes to mainly oblongs and squares; diverse infrastructure forms such as triangles have been transformed to standardized network configurations (Graham & Marvin 2001).

Parallel to networks, technological changes and new travel modes have emerged and influenced new transport network design, like horses and carriages, ships and canals, railways, cars and airplanes. Gruebler (1996) evaluated the diffusion of new transport mode technologies and historical transformation of major transport modes; different modes require and use different transportation infrastructure. Barnett (1995) showed that population growth processes and land use developments are connected with transportation networks and travel mode changes in the United States. Considering different transport modes, Gil (2014) proposed a multimodal urban network model to explore the structure of a city-region, combining metrics, distances and additional city information. Proposed multimodal network evaluation explains different phenomena in network design and provides a more complete profile of the urban form.

Given these past and ongoing developments in transport modes, it is important to foster overall understanding about mode characteristics and network design and further enhance planning methods as needed. Due to the variety of real-world network patterns found above and ongoing technological changes, this research aims at a generic planning framework, including evaluation methods, to support planning and efficient network infrastructure.

1.1 Current network design and planning practice

Many different approaches are applied in transportation planning and network design; scenario-based planning is often employed in planning practice. In scenario-based planning, the future scenario is determined with highest estimated returns under given budget constraints from a set of previously generated alternative scenarios. Evaluation then relies mainly on quantitative or qualitative methods, e.g. cost-benefit analysis or cost-effectiveness analysis and includes a planning objective, e.g. a sustainability objective. A choice of a most efficient alternative is made under given budget constraints. A key advantage of this scenario-based approach is its direct comparison of various scenarios. However, potential new infrastructure is evaluated separately from other infrastructure investments, either in the future or at other sites. Evaluation also takes place without any all-encompassing and long-term ‘visions’ or concepts, considered a disadvantage for a scenario-based approach.

A scenario-independent approach is given by norms and guidelines based on general recommendations for network design. Norms and design guidelines are currently used platforms with recommendations for both transportation network design and urban planning. Road network design guidelines (e.g. VSS 1994; IHT 1997; AASHTO 2004; FGSV 2008; ITE 2008) included discussion about some aspects of urban design and network topology and the ‘Urban Street Geometry Design Handbook’ (ITE 2008) focused on road types and hierarchical design, conflict points at intersections and intersection spacing. ‘A Policy on Geometric Design of Highways and Streets’ (AASHTO 2004) proposed hierarchical designs and highlighted technical design and road geometry. The ‘Planning and Urban Design Standards’ (American Planning Association 2006) also defined hierarchies and connectivity within network design. High connectivity is recommended for future city design and discussed for multiple urban layouts. However, despite much discussion, no recommendations included detailed information on their corresponding effects. So, stated rules are rather like ‘rules of thumb’; uncertainty remains in application specifics and therefore weakens norm-based planning applications.

Piecemeal methods for transportation and urban planning are often classified as bottom-up planning. The norms described above refer to piecemeal planning, as well as the proposed grammar framework below. While bottom-up planning refers to single elements and piecemeal assembling of these elements, top-down planning includes an initial and centralized, but complete, plan of an area. Despite these differences, top-down and bottom-up planning can both share objectives and constraints; both can result in a well-functioning city and transportation infrastructure. However, implementation and construction of a complete top-down plan normally takes a long time – even longer than a governmental mandate period – because (1) political consensus must be reached before plan implementation, (2) building costs are very high and (3) potential land acquisition takes additional time before construction. Additionally, the concept might change between mandate periods. In contrast, bottom-up planning is conducted more continuously and results in a natural network growth, but still relies on planning consensus. This research proposes a bottom-up planning approach based on the grammar method, as highlighted in the following section.

1.2 Grammar-related network design

Grammar-related design methods are similar to norms and guidelines mentioned above, but provide a more generic framework and well-defined components. Grammar-related design methods have been applied for decades and have proven to be promising for urban design, planning and transportation networks; in the following section, they are introduced and relevant literature is summarized. A grammar is defined as a set of syntactic rules and corresponding specifications of these rules; rules describe how elements, like transportation network, intersections or street segments are connected for efficient final use and application (a more complete definition is given in Section 2.1).

Grammar-related planning methods have been used for a long time in architecture, urban and transport fields, with variations. Explicitly or implicitly applied grammars appear in many eras of architecture. For historical evaluation, Stiny & Mitchell (1978) determined rules for the Palladian villa style based on building geometries of a ground plan. Dylla et al. (2008) rebuilt ancient Rome based on rules extracted from building geometries and procedural methods, originally from floor plans, images and statistical data. Stiny (1985) visualized rules for a prairie house from Frank Lloyd Wright. March (1976) evaluated buildings and translated design to a Boolean code, including rules. LeCorbusier (1955) even applied a strong hierarchical approach for road design to city planning, similar to a rule-based approach. However, grammars are also proposed for future planning applications. The new urbanism movement often defines its ideas in codes and rules (Dutton 2000; Haas 2008) and its ideas are applied around the world (e.g. Duany, Plater-Zyberk & Alminana 2003). Rules have been applied in computational-based procedural applications (e.g. Duany, Sorlien & Wright 2009), for new and existing developments.

Grammar rules are also applied in urban and transport planning. Marshall (2005) determined rules for intersection type choice and road hierarchies for network design based on qualitative evaluation; van Nes (2003) suggested rules for road densities based on travel cost calculations and quantitative optimization. Yerra & Levinson (2005) discovered emergence of hierarchical network structures and proposed local capacity investment rules. Alexander, Ishikawa & Silverstein (1977) stated different rules, such as a 3-arm intersection recommendation; however, they also referred to patterns, which define a final state, e.g. a final city plan. Kaisersrot (2011) and the ‘SmartCode’ (Duany et al. 2009) both applied specific rules in their research and were able to improve livability, orientation and perception of a city. Recently, more software products have increasingly implemented procedural modeling approaches in multifaceted urban planning environments (e.g. Vanegas et al. 2009, ESRI 2016, Lienhard et al. 2017). Vitins & Axhausen (2016) summarized and compared major grammar-related contributions from different disciplines and perspectives.

Grammar-related planning has multiple advantages. Grammars provide applicable recommendations for planning purposes, which are highly adaptive to different sites. Grammar-related planning also consolidates planning recommendations within disciplines, as opposed to isolated, complex and very specific solutions. Grammars from different disciplines can be merged into an even larger set for planning recommendations (e.g. from urban or transport planning, and architecture). Low application costs encourage application of grammars in planning projects (Parish & Müller 2001; Watson et al. 2008; Lienhard et al. 2017); grammars can be implemented in interactive planning tools (e.g. Jacobi et al. 2009; Weber et al. 2009; Smelik et al. 2014). Grammars are able to retain and preserve consensual urban planning intentions and visions for longer time periods and are applicable step by step in a bottom-up approach; however, they are also applicable for top-down infrastructure investment policies. Even though resources and infrastructure improvements are implemented gradually, grammars define a planning guideline for long-term direction and planning guidance. Approved guidelines supported by underlying explanations are thus essential for progress toward efficient and well-functioning cities with transportation networks as their ‘backbones’.

Grammars are applied when designing new networks from scratch. A network is then built up by choosing rules, with their distinct application specifications, to reach given planning goals, such as low travel costs. However, grammars are also suitable for transitions and redesign of existing networks. Utilizing specific knowledge about their effects, grammars can improve existing topologies; for example, intersection types can be replaced (roundabout vs. signal vs. right-of-way intersections). Network segment capacities (e.g. number of street lanes) can be added or removed, depending on grammar and specification. Thus, even when a network topology exists, a transition is still possible to fulfill new or changing user requirements, another advantage of the generic grammar approach.

Disadvantages of grammar-related planning include unspecified effects in project applications. Grammar rules’ impacts are not always accurately assessed, as rules are often based on scanty evidence and prior conclusions. Grammars might represent rules of thumb, common understanding, human perception and aesthetic preferences; validation is thus needed for consolidation and appropriate application; e.g. new urbanism ideas often lack quantitative evaluation. Proposed grammar-related ideas often miss a link to the economic benefits of a transport network (cost efficiency, reliability, etc.) and an objective and corresponding quantitative measure related to primary travel needs (see also network design limitations below). Besides incomplete assessments, many grammars lack clear and coherent definitions, which hamper rule consolidation within and across disciplines. Grammars require specific and clear notation for their rules, as well as information about their application range. Clear notation also clarifies future application in case of prospective, unknown changes; e.g. in transportation network design, it is important to know about required network design changes should transport modes evolve and new technologies for transport vehicles emerge. Only then can grammars effectively respond to these future changes.

1.3 Current planning limitations and research needs

In addition to key advantages of transportation networks related to economic and societal benefits, we know about their limitation (summarized below) and disadvantages, which must be addressed when designing them and when proposing new planning methods. Limitation 1 refers to generalized costs for building and using transport networks, especially time, monetary costs and discounted infrastructure costs. This would also include external costs in a wider sense, such as safety, pollution, noise and dependencies on resources and land consumption. Practically, societies – as well as individuals – are constrained with regards to cost; they seek cost reductions to maximize benefits and overall welfare. Generalized cost optimization aims to address limitation 1. Limitation 2 refers to capacity and space constraints of any transportation network, which are limiting factors, especially in urban and agglomeration areas with high population densities and high travel demands. Infrastructure capacity is also limited, especially for historically grown network infrastructures embedded in built environments. Historically grown networks are often the basis for existing technological developments, as well as future developments. Like limitation 1, changes in technology and future technological development can alter capacity within limits, given capacity and space constraints. Limitation 3 refers to travel demand changes due to land access and growth, seen in growing agglomerations (Venables 2007) and as a result of rural depopulation in remote and increasingly abandoned places (e.g. mountainous areas). Future travel demand changes are difficult to predict, due to uncertainties in travel motivation and cost development (e.g. economic purchasing power). Summing up, all three limitations underline not only the importance of network design, but also the underlying complexity and dependencies. The overarching goal is to address these limitations and provide optimal solutions within these limitations.

Given the undoubted relevance of transportation network design, many different methods exist for planning transportation infrastructure. However, many research contributions relate only to a subset of above limitations, such as network design algorithms focusing on cost optimization. This research moves to bridge the gap in network design and consider all the above limitations, using the proposed grammar methodology as much as possible. Because of overall complexity, discussion of all limitations in detail is not feasible, but this research provides a methodological framework to further expand certain elements, adding references for further information.

1.4 Research aim

This exploration contributes to a quantitative understanding of urban network design and dependencies between topologies, intersections, urban densities, flow and variable travel demand, travel modes and optimized infrastructure investments. It also combines design and technical requirements for efficient grammar-related planning methods, with the following aims:

1. (1) Notation of a generic grammar-based framework for network design planning rules and related planning fields (e.g. general transportation planning, urban planning, and architecture).

2. (2) Systematic evaluation of complex and interdependent grammars’ effectiveness, to gain knowledge about the benefits of grammar implementation and enhance efficient rule application in practice.

3. (3) Tackle discussed limitations (Section 1.3): generalized cost reduction during network design, current and historically grown network and capacity limitations and uncertainty in travel demand.

Quantitative methods are required to achieve these objectives and evaluate proposed grammar rules, allowing statistically valid results (e.g. for graph vertices and edges $G(v,e)$ ). Quantitative methods also determine network flow, turn delays and overall performance (e.g. travel times), and topology measures for specific network forms and properties, including non-metric information (e.g. Marshall 2005). Overall performance is crucial for competitive network design; the proposed methods aim at specific optimization procedures to tackle the issues above.

1.5 Verification of proposed methods

To reach the stated research goals, this work focuses on network design and network topology. This research specifically considers effects of intersections, which have considerable impact on overall network design and efficiency (e.g. travel costs), especially in dense urban areas. Intersection types and delays have often been ignored in network-related research, probably due to missing data, complexity, or perceived lack of importance for certain studies. This research underlines the importance of intersections in urban networks and fills a gap about effects of different intersection types on network topologies.

Intersections are omnipresent in transport networks; this is where traffic flows cross, merge, or diverge at intersections and different transport modes meet. Intersections and approaching lanes require considerable amounts of urban space. Intersections and network topology are strongly coupled, e.g. regarding the number of arms per intersection (also called cardinality or node degree) or traffic flows. Intersection type choice plays an ever-larger role due to increasing urban densities, intensifying traffic flows, relatively smaller budgets for land acquisition and infrastructure reconstruction and improvement. Government investments and costs are higher in urban areas than rural areas (Florida Department of Transportation 2014). Often, relatively low average speeds for cars are measured (compared to free flow speeds), underlining turn delay and intersection relevance. Therefore, integration of intersection type choice in network design is essential for transport and urban design.

This article focuses on urban transportation network planning and intersection type choice using quantitative evaluation and technical methods. Travel demand and flow are important because of delays and economic travel costs, and travel demand interacts with land use; it is estimated using rates for specific land use patterns. Increasing population density is also considered in sensitivity analysis, relevant for demand forecasts with uncertain assumptions. A new evaluation method is proposed for growing population densities, maximizing capacity of an entire network and travel demand a network can support, which is related to maximum population growth. However, urban transportation networks are also connected to given economic and societal structures, as Hillier et al. (1976) explained; network design is influenced by social and economic influences, similar to hierarchical network design in a growing capitalistic world. However, this manuscript excludes societal demands and interaction, such as economic influences, safety issues or quality of living; additional research would be needed on these interfaces, to merge additional grammars to an even larger and more encompassing set.

2 Methodology

Grammars and rules are applied in different applications and contexts. Formal definitions are provided in the following for grammars related to transport and urban planning; comparison with other fields shows transferability of the proposed definitions, providing an opportunity for grammar consolidation. Notation below refers to syntax and semantics, important because of their integral role in all grammar definitions. This section also presents an evaluation methodology to measure effects of grammar rules, because knowledge of grammars’ quantitative effects improves efficient implementation in all planning processes.

2.1 Grammar definition and notations

2.1.1 Syntax

Many formal definitions exist for syntax in different disciplines; please refer to Vitins & Axhausen (2016) for additional references. The following definition utilizes major components of an early instance (Chomsky 1956, 1959), adapted for planning purposes. $\unicode[STIX]{x1D700}$ is a finite set of non-terminal elements $e$ . ${\mathcal{R}}$ is a set of rules $r$ based on notation $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x1D6FD}$ , where $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\in \unicode[STIX]{x1D700}$ . Syntax $R$ describes – in the form of a finite number of rules – how elements $e$ are added recursively to each other. Rules $r\in {\mathcal{R}}$ describe how a given design, its elements and geometries are transformed to another design with added or modified design elements, such as network segments. $\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FD}$ is valid, meaning that element $e$ cannot be transformed in itself because then further network development and transformation are inhibited, e.g. for network growth or any other network changes. Moreover, $\unicode[STIX]{x1D6FC}\rightarrow \{\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\}$ , and $\{\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\}\rightarrow \unicode[STIX]{x1D6FD}$ are valid, because network design grammars are non-reversible. $R$ includes rules to stop the process. Summing up, $R$ is responsible for the ‘mechanics’ of a specific design proposition. A stand-alone set $R$ without additional information is called context-free syntax (Chomsky 1956, 1959).

2.1.2 Semantics, grammars and language

Many formulations exist for semantics in different fields; and even though there are slightly different, they follow a similar purpose of complementing a given syntax. Gunter (1992) reviewed semantic expressions from mathematical and programming perspectives and also refers to other languages. Like Gunter (1992), Winskel (1993) stated that semantics of an arithmetic expression are responsible for describing the expression’s precise meaning. Ihaka & Gentleman (1996) defined the syntax and semantics for programming language $R$ . Stiny (1985) referred to syntax and semantics of urban form when mentioning grammars. Beirão (2012) also referred to shape grammars and semantics. He highlighted the ‘missing interpreter’, similar to the missing semantics cited above, as did Fleisher (1992), who also recognized the failure of missing linkage between grammar rules and semantics. Moreover, Beirão (2012) stated that literature addresses rules, but the rules are difficult to apply because they lack meaning and interpretation. This acknowledged problem highlights the difficulties of applying grammars correctly. Summing up, semantics exist in different fields with slightly different formulations, but agree in interpreting the rules to produce a meaningful outcome.

Beside ${\mathcal{R}}$ , this paper also defines application specifications ${\mathcal{S}}$ , mirroring semantics, required for rule applications. Here, ${\mathcal{S}}$ is highlighted because a given syntax ${\mathcal{R}}$ might be insufficient to generate a desired outcome. ${\mathcal{S}}$ refers to information about application guidance of ${\mathcal{R}}$ . ${\mathcal{S}}$ is comparable to semantics in linguistic-related or programming terminology. $s\in {\mathcal{S}}$ complements specific rules $r\in {\mathcal{R}}$ and includes all information, except the rules themselves. In particular, ${\mathcal{S}}$ contains information about effects of ${\mathcal{R}}$ on efficiency, or safety, etc. Moreover, ${\mathcal{S}}$ specifies the application range for ${\mathcal{R}}$ for a reasonable design. Applying rule $r_{1}$ repeatedly under identical application specifications $s_{1}$ leads to identical outcomes, whereas a different application specification $s_{2}$ might lead to different outcomes. Here, semantics ${\mathcal{S}}$ and rules ${\mathcal{R}}$ refer to fundamental principles and characteristics of transport planning and behavior, such as speed, capacity, topology and – generally – the use of space in transportation.

Grammar ${\mathcal{G}}$ is a 2-tuple consisting of ${\mathcal{R}}$ and ${\mathcal{S}}$ : ${\mathcal{G}}({\mathcal{R}},{\mathcal{S}})$ and combines rules with their meaning. Language ${\mathcal{L}}$ is defined as set of ${\mathcal{G}}$ and $\unicode[STIX]{x1D700}$ : ${\mathcal{L}}({\mathcal{G}},\unicode[STIX]{x1D700})$ , thus including all grammars $g$ and all building elements $e$ . This formal definition is applicable for an urban design language, as shown below. It is also suitable for other languages and still works for linguistics, where words are elements of $\unicode[STIX]{x1D700}$ and grammars are elements of ${\mathcal{R}}$ , with meanings ${\mathcal{S}}$ .

The expression ‘shape grammar’ is frequently used in design contexts such as network or urban design; it was propagated by Stiny & Gips (1972). ‘Shape’ tends to refer to geometric elements and is therefore slightly ambiguous in a transport network context, because grammars do not apply exclusively to physical shapes, but also to certain functionalities, like speed limits for road types and priority rules at intersections. Therefore, shape grammars are a subset of all grammars, referring specifically to shapes, usually applied in architecture.

Overall, the grammar notation above offers immense potential; any grammar fits into the proposed schema and can also be applied efficiently in design and planning tasks.

2.2 Study designs for grammar evaluation and extraction

Knowledge about grammars’ effects is important in planning due to necessity of efficient transportation infrastructure. Two distinct approaches are proposed below for grammar evaluation. The first approach (study design 1) is applied when a grammar rule is accepted as well defined and when evaluation is needed to measure its effects. The second approach (study design 2) extracts and evaluates new grammars.

2.2.1 Study design 1

Study design 1 evaluates grammars’ effects, thus assuming a preexisting formal grammar definition. Study design 1 proposes implementing grammars in diverse design applications to evaluate their results. Figure 1(a) visualizes a single process of an evaluation for generic grammar $g_{0}$ and grammar $g_{1}$ , including a statistical comparison of the resulting designs. Statistical comparison allows measurements of $g_{0}$ and $g_{1}$ grammar effects relative to each other. Designs based on grammar $g_{1}$ might outperform (see Section 2.3 for explanation) designs with grammar $g_{0}$ , or vice versa. Therefore, it can be stated that a certain grammar is able to outperform another grammar in the resulting designs. Methodology displayed in Figure 1(a) requires a repetitive design evaluation; $g_{0}$ and $g_{1}$ are not only applied in a unique design application, but grammars are applied repeatedly to achieve statistically significant comparison results. Additionally, reference networks are added for further comparison.

Two examples of such evaluations with study design 1 are provided in Figure 1. Figure 1(b) refers to public transport networks described with many variables, such as stop interval distance, or line density. Figure 1(b) shows three public transport networks manually designed according to certain characteristics (Estrada et al. 2011). These networks are evaluated and compared to ascertain an objective function. Additional parameters are also evaluated, like stop interval distance. Figure 1(c) refers to Eichler, Bar-Gera & Blachman (2012), who determined specific intersection types and turn configurations, as well as evaluated network patterns in numerous example gridiron networks. Eichler et al. (2012) essentially applied study design 1 and evaluated resulting networks for travel distance changes.

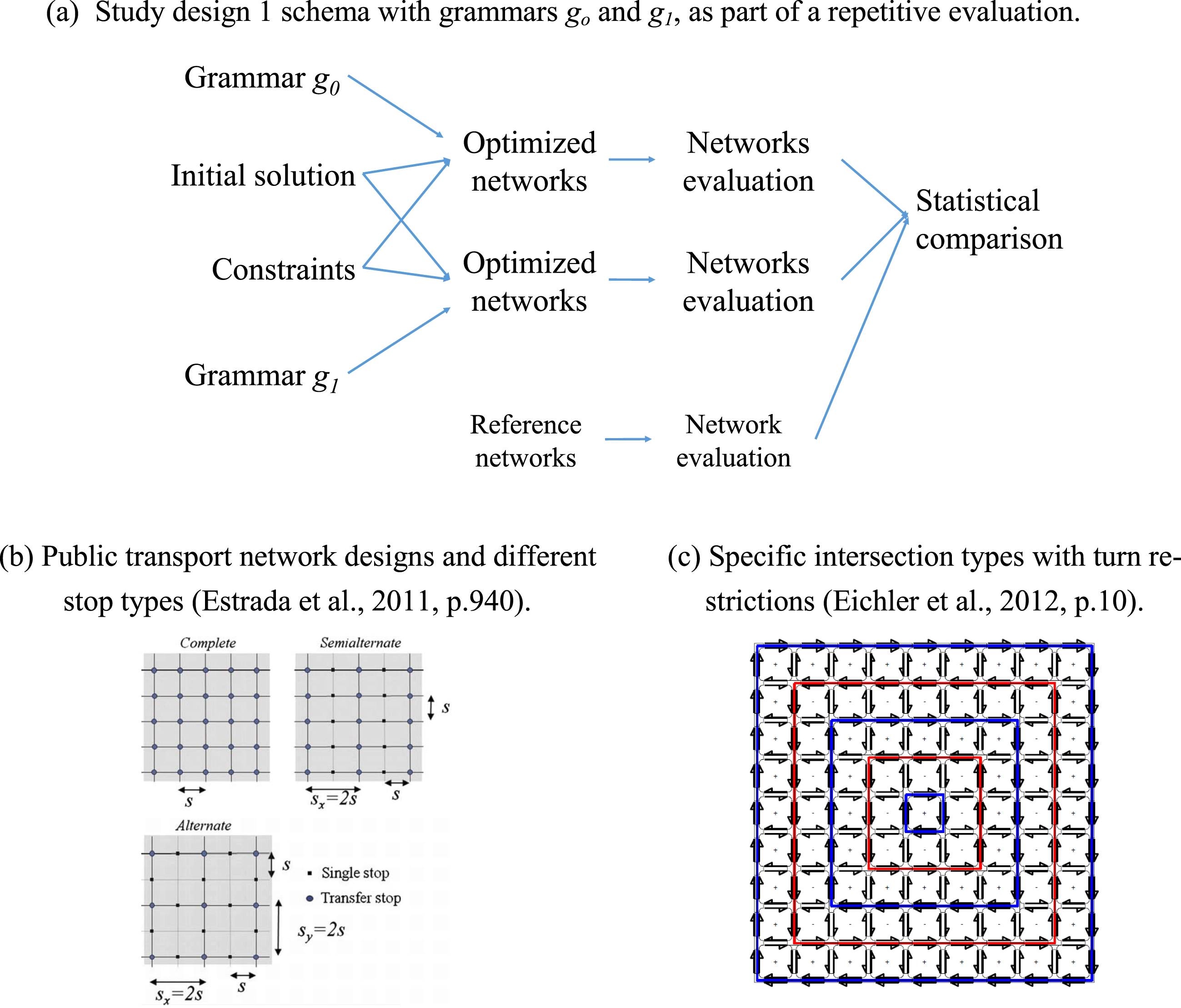
Figure 1. Study design 1, overview and example application similar to proposed methodology.

2.2.2 Study design 2

Study design 2 assumes certain characteristics occurring in (optimized) network designs, which can be determined and extracted for future recommendations and grammar rules. New grammar rules are obtained and established based on these optimal network designs (see methodological schema in Figure 2(a)). Unlike study design 1, grammars are not pre-defined beforehand, meaning that optimized designs are statistically evaluated for potentially significant characteristics. Again, multiple designs are needed for statistical analysis and reliable results. New rules are extracted and statistically justified under various transport conditions and reference networks are compared. Figure 2(a) shows a schema of proposed study design 2.

Figure 2(b)–(e) shows examples of study design 2 using similar methodologies, but only implicitly referring to grammars. Figure 2(b) and Figure 2(c) refer to spatial optimization methods, whereas Figure 2(d) and Figure 2(e) refer to statistical evaluations. Figure 2(b) shows results of Kaisersrot (2011), which simulated and evaluated urban scenarios iteratively by applying parcel relocation and optimization dependent on certain exogenous parameters; an underlying algorithm designed and optimized urban scenarios. Figure 2(c) shows an example network on a featureless plane with evolutionary structures, evaluation and investment models for optimized road type choice. Both examples in Figure 2(b) and (c) optimize scenarios based on infrastructure changes. In study design 2, it is also suggested that network characteristics are extracted using statistical methods from optimized scenarios. Figure 2(d) and (e) depict two example approaches, each focusing on statistical evaluation of network characteristics. Figure 2(d) shows real-world parcel shape distribution, based on multiple existing road networks. Figure 2(e) depicts angle distributions of adjacent edges in a descriptive evaluation of historic Paris networks.

As seen in study design 1 and 2, grammars are evaluated with an optimization method (explained below in more detail). This is because grammars only describe a certain part of the design process, leaving the remaining design process to other grammars. An optimization method is also required for single grammar evaluation, since the additional network beyond a single grammar application needs to be well designed and optimal for evaluation.

Figure 2. Study design 2, overview and example application similar to proposed methodology.

2.3 Quantitative evaluation of network designs

A major advantage of grammar-related design is the ability to collect grammars from different fields for a set of comprehensive planning recommendations. Using the entire set of grammar rules, planners are then able to generate subsets of rules suitable for specific projects and planning sites, e.g. related to urban planning or transportation. Thus, knowledge about grammar rules and application specifications allows planners to narrow the entire set of rules to a well-defined subset for specific planning sites and projects. The goal is to derive an optimized subset of most relevant grammar rules to support planners’ objectives.

Urban planning objectives often include one, several, or even combined goals with either an economic, social or environmental focus. In a grammar-based approach, planners are able to apply rules to reach these objectives, especially if rules’ effectiveness and their application specifications are known. Grammar rules are thus assessed using the following two methods.

2.3.1 Elasticity-based grammar evaluation

This proposed grammar evaluation method applies marginal effectiveness and elasticities for measurements of grammar effectiveness. Elasticity is a robust measure to assess responses of an observed variable. Multiple examples of elasticity calculations already exist in urban and transport planning (e.g. Cardillo et al. 2006; Ewing & Cervero 2010; Weis 2012), related to energy consumption, emissions, generalized travel costs, quality of urban space and residents’ satisfaction (e.g. Bramley & Power 2009); Vitins & Axhausen (2016) proposed elasticities for network design grammars.

Marginal changes of a dependent variable are related to changes of an independent, descriptive variable. In the proposed method, dependent variable $o$ equals, e.g., user costs and independent variable equals an underlying investment change $\unicode[STIX]{x1D6FF}i$ : $\unicode[STIX]{x1D6FF}o/\unicode[STIX]{x1D6FF}i$ . In grammar context, marginal costs describe efficiency of a specific rule on a given effectiveness measure. Elasticities are free of units ( $\unicode[STIX]{x1D700}=(\unicode[STIX]{x1D6FF}O/\unicode[STIX]{x1D6FF}I)\cdot (\bar{I}/\bar{O})$ , when assuming linearity), facilitating comparison between different studies (such as Ewing & Cervero 2010). Determination of elasticities requires data collection and quantitative data processing based on the formula above, as shown in the results section.

2.3.2 Maximum network supply method

It is widely acknowledged that transport network cost efficiency is crucial. Evaluation methods determine travel cost effects dependent on capacity investments, e.g. cost-benefit analysis. However, costs remain unclear when estimated future travel demand and flows exceed expectations. Authorities are confronted with this situation whenever their road networks are saturated, e.g. due to different travel behavior or increasing urban densities. A planning approach is proposed in the following to tackle this problem.

Proposed Maximum Network Supply Method accounts specifically for unknown future travel demand. In infrastructure planning processes, planners might be uncertain about future population and job densities’ travel effects and behavior. Therefore, it is essential to know how much density one network can support without a politically unacceptable travel time increase ( $\unicode[STIX]{x1D6E5}t^{x\%}$ ). The proposed method assesses maximum increase in urban density $\unicode[STIX]{x1D6E5}d_{\mathit{structural\, data}}$ ( $\unicode[STIX]{x1D6E5}t^{x\%}$ ) a network can support, without any unacceptable travel time increase $\unicode[STIX]{x1D6E5}t^{x\%}$ , where $d$ represents urban density (jobs, population, etc.). The focus is on travel time, due to its major role in transport cost-benefit-based evaluation. An upper limit determines maximum travel time increase (20% in the following $\rightarrow \unicode[STIX]{x1D6E5}d_{\mathit{structural\, data}}$ ( $\unicode[STIX]{x1D6E5}t^{20\%}$ )) achieved by gradually increasing urban densities. An average peak hour demand defines a starting point for this method, based on census data. Obviously, travel demand depends on other elements as well: time of day, mode share, or car occupancy, all of which are ignored for simplicity’s sake in this evaluation. The aim is to determine effects on overall travel time changes for a given network; however, these dependencies are examined indirectly with this proposed method.

This method’s major advantage is its focus on the relative difference in travel times; absolute travel demand is less important. Therefore, this method is also more suitable for future and less certain planning projects; it differs from traditional approaches with precise assumptions on future travel demand, despite the element of uncertainty. Additionally, proposed Maximum Network Supply Method provides insights on evaluated networks: for example, for such criteria as meshedness or intersection type choice (Sections 3.1 and 3.3), which are then evaluated statistically, enabling the verification of the grammars defined. Therefore, dependencies are examined between $\unicode[STIX]{x1D6E5}d_{\mathit{structural\,data}}$ ( $\unicode[STIX]{x1D6E5}t^{x\%}$ ) and network characteristics and shown in the result section.

3 Network design specifications

Overall, this research focuses on transport network design in dense agglomerations of bigger cities ( ${\gtrsim}1$ Mio. inhabitants including their agglomeration). This section provides details on assumed network characteristics, travel demand patterns, topology design and evaluations.

3.1 Intersections

In transportation, queue lengths at intersections and delays are essential elements in planning and design, e.g. for economic evaluations. Obviously, other criteria, such as safety, cause major challenges as well; however, safety is ignored here to minimize complexity. Intersection delays are evaluated first; implications for different modes are discussed consecutively afterward.

An example is used for initial intersection comparison, similar to e.g. Yang & Yagar (1995) or Gartner, Messer & Rathi (2002). In this first example, turn delays are evaluated for different flows on different turn movements to gain additional insight into turn delays at different intersection types. Clearly, turn delays depend on flows of other turn movements. More specifically, the proposed example focuses on through traffic, crucial in planning. Proposed measure $\unicode[STIX]{x1D70F}$ is sensitive to through traffic flows crossing a given 4-arm intersection from one approaching arm to an opposing arm. More specifically, $\unicode[STIX]{x1D70F}$ compares increasing $q_{east}$ and $q_{west}$ flows (through movement) with a reference situation of equally distributed flows $q_{r}$ on all 12 turn movements (Figure 3, and Equation below), excluding U-turns. $\unicode[STIX]{x1D70F}$ is suitable for sensitivity analyses of various intersection types under different flows $q$ .

$$\begin{eqnarray}\unicode[STIX]{x1D70F}=\frac{((q_{east}+q_{west})-2\cdot q_{r})}{q_{r}\cdot v(v-1)+(q_{east}+q_{west})}\quad \text{whereas }\{q_{east},q_{west}\}\geqslant q_{r}.\end{eqnarray}$$

$\unicode[STIX]{x1D70F}$ : Through traffic share ( $0\leqslant \unicode[STIX]{x1D70F}\leqslant 1.0$ ); $v$ : Number of arms; $q_{east}$ , $q_{west}$ : Flow of through movements on east–west axis (Figure 3); $q_{r}$ : Flow on all other turn movements.

Vehicles from north and south must yield to vehicles from east and west (Figure 3) at right-of-way intersections. Evaluations on 3-arm intersections exclude the northern arm in Figure 3. Angles between approaching arms are ignored due to their minor influence (HCM; Transportation Research Board 2010).

The following consequences are defined based on the formula above and description:

1. (i) $\unicode[STIX]{x1D70F}=0\%$ if $q_{east}$ , and $q_{west}$ equal the flows of other 10 turn movements.

2. (ii) $\unicode[STIX]{x1D70F}>0\%$ if there is increasing through traffic on the east–west axis. $\unicode[STIX]{x1D70F}=100\%$ if there are traffic flows only on the east–west–east axis $q_{east}$ and $q_{west}$ .

Section 4.1 shows values for $\unicode[STIX]{x1D70F}$ at various intersection types.

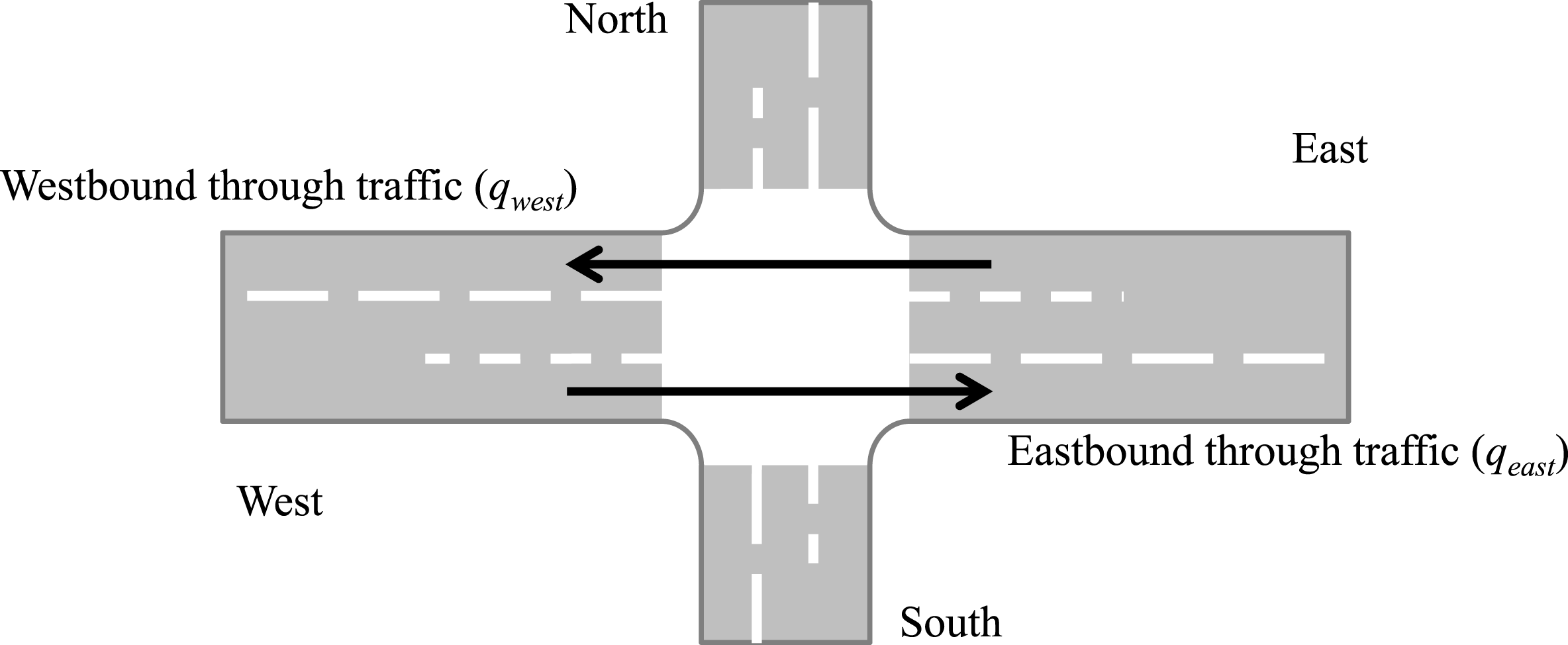
Figure 3. Experimental design for sensitivity analyses of through traffic, with priority for east–west and west–east traffic flows and two approaching lanes at each arm.

3.2 Network specifications

Table 1 shows assumed capacities, free flow speeds and approaching lanes for roads and intersections of different road hierarchies. Scenario 0 refers to a default scenario with relatively low capacities, while capacities of roads and intersections increase for sensitivity analysis in scenarios 1 and 2. Capacities and speed distribution are set according to Swiss standards. Intersection capacity is calculated according to HCM (Transportation Research Board 2010). Road hierarchies are defined for roads within a given network according to a greedy algorithm (Vitins 2014).

Table 1. Road and intersection capacities in three distinct scenarios

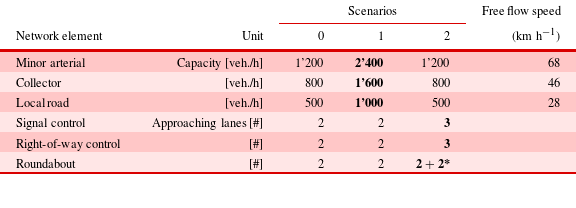
*: 2 incoming lanes and 2 circulating lanes

3.3 Meshedness

Network topology is essential for travel reliability, robustness and resilience (e.g. Erath 2011; Helbing 2013). Multiple measures exist for topology evaluation, but redundancy is an essential factor, reducing congestion, lowering travel times and improving reliability in case of network failures. Faces (regions enclosed by planar graphs) are elements of redundant networks and should be considered further. Meshedness coefficient $M$ (Buhl et al. 2004; Courtat, Gloaguen & Douady 2011) accounts for redundancy; $M$ is a sensitive graph topology measure defined as $M=F/F_{max}$ , where $F$ is the number of faces of a network graph, and $F_{max}$ is the maximum possible number of faces in a maximally connected planar graph ( $F_{max}=2\cdot N-5$ ), proportional to number of nodes $N$ (see Cardillo et al. (2006) p. 5).

$$\begin{eqnarray}M=\frac{F}{2\cdot N-5}.\end{eqnarray}$$

3.4 Travel demand generation

Both travel demand independent – and dependent – network evaluations can be found in the literature and practice. Demand independent evaluations are applied, for example, in space syntax approaches (Hillier et al. 1976; Xie & Levinson 2007) and measures of network topologies like centrality and dendritic representation, or in empirical network evaluation methods, such as Cardillo et al. (2006) or Barthélemy (2011) or experimental approaches (Eichler et al. 2012). A demand-based approach is proposed in this article, since grammars for urban networks, especially intersections, depend on flows and, indirectly, on urban densities. Modeling travel demand is a complex endeavor when considering time of day, transport modes, destination choice and long-term decisions like home and work location choice. Changing home locations, costs and land prices influence travel behavior, but are not yet understood and modeled in all details. Moreover, trip generation and distribution can vary significantly and complicate specific descriptions of corresponding trip rates; Schneider, Shafizadeh & Handy (2014) observed large variances in trip generation rates provided by the Institute of Transportation Engineers (ITE), depending on dwelling type. A robust and straightforward methodology is thus important to estimate travel demand, and additional evaluations complement demand sensitivity and their effects (Section 2.3.2).

The following examples assume travel demand generated evenly over the entire study area (similar to e.g. Yerra & Levinson 2005). Long-distance travel, causing additional complexity, is ignored because it requires large-scale highway hierarchy levels with different characteristics and requirements, as opposed to urban networks emphasized in this paper; our research applies a straightforward demand estimation method, knowing, but ignoring more detailed demand definitions. There is also potential for larger areas and larger networks, especially with computational advances (calculation speed), using the same methodology for larger areas; an early example is given in Vitins, Schüssler & Axhausen (2011).

Table 2 lists relevant travel demand estimation parameters as default values for the following calculations. Values in Table 2 refer to a medium-dense neighborhood in Zurich, Switzerland. Additional sensitivity analysis simulates growth processes based on the above Maximum Network Supply Method.

Table 2. Assumed variables and values for travel demand estimation

Source: $^{(1)}$ Amt für Raumentwicklung, Baudirektion Kanton Zürich (2012)

$^{(2)}$  Swiss Federal Statistical Office (BFS) (2012)

3.5 Network topology design algorithm (IACGA)

This article proposes a systematic statistical examination of optimized networks and grammars focusing on specific network characteristics. Optimized networks are required for statistical extraction of grammars from given optimized networks and their characteristics; certain patterns might evolve more frequently than others during an optimized design process (study design 1, Section 2.2.1). However, grammars also can be implemented during an optimized design process (study design 2, Section 2.2.2). Therefore, an optimized design method is briefly summarized in the following.

An efficient design and optimization algorithm, IACGA, is proposed and outlined in this section. The proposed algorithm relies on an optimization methodology specifically applied for network design. This design process requires sophisticated and cumbersome optimization; however, resulting patterns are then statistically evaluated under various conditions and sensitivity analyses. Moreover, resulting patters are independent from real-world case studies (and historical developments) when applying a design algorithm to design new networks and evaluating them with statistical measures.

The applied network design algorithm (IACGA) is based on an integrated ant colony optimization (ACO, e.g. Dorigo & Stuetzle 2004) and a genetic algorithm (GA, e.g. Goldberg 2002), allowing network design, using a predetermined set of candidate road segments. In this article, optimized networks are designed from an available larger set of road segments on a dense gridiron pattern (see Figure 6(a)), also allowing a reasonable comparison between newly designed networks and predetermined network patterns (see result section). Only rectangular approaches are considered for this analysis, because angles of intersection arms are less relevant when it comes to turn delays (see above, or HCM; Transportation Research Board 2010).

This IACGA algorithm applies an iterative procedure and uses information on success or failure of all previously generated networks to suggest more (cost) efficient networks. It starts with randomly generated networks of generally low efficiency; a set of about 100–1000 networks is called ‘population’ and is evaluated in parallel each iteration, similar to a GA. For each iteration, a recombination procedure recombines networks for an offspring generation. For each new network, potential candidate network elements are chosen according to a probability function from selected networks of a parental population and its individuals. In a first iteration, the probability is set randomly. However, in all consecutive iterations, a defined probability function chooses candidate elements, accounting for the success of all networks designed in previous iterations. If a candidate element already implemented in previous iteration networks with high success (high cost efficiency) is under consideration, it is more likely that this candidate element will be chosen again. Information about cost efficiency is stored for each element and mirrors ACO pheromone information. Cost efficiency increases during all IACGA iterations and converges to a high cost efficiency of practically all networks within a population. For more details the reader is referred to Vitins et al. (2013), Vitins, Schüssler & Axhausen (2012) and Vitins (2014); this article focuses on verification and evaluation of the resulting optimized networks.

Applied design algorithm implements a heuristic approach because of the large search space in network design, meaning that the applied algorithm is unable to guarantee finding the most efficient network patterns; this algorithm potentially generates less efficient networks than those based on a global optimum. However, only minor variations occur in the optimized networks and specific patterns might still emerge as networks close to a global optimum. This proposed algorithm cannot cope with infinitely large networks, because of increasing search space size and demands. The size of the generated network is, however, large enough to extract characteristics and small enough for reasonable calculation time.

4 Results

Section 4.1 summarizes characteristics of isolated intersections, detached from surrounding networks. Evaluation of isolated intersections serves as a solid foundation for more complex evaluation of entire networks (Section 4.2). Section 4.3 still considers intersection types, but focuses on network topology evaluation. Sections 4.2 and 4.3 refer to the two study designs defined in Section 2.2 and employ the IACGA. Section 4.4 shows results of the Maximum Network Supply Method.

An introductory example below underlines the significance of network design, intersection type choice and urban planning on transportation economics. Different grid patterns are evaluated with and without turn delays. Like the Maximum Network Supply Method (Section 2.3.2), travel demand in this example varies to deliberately exceed capacity and evaluate corresponding travel time changes. Figure 4 shows results of different grid patterns when through streets are removed, reducing road density. As expected, Figure 4 shows higher average travel times at lower network densities when ignoring turn delays (Figure 4a). However, travel time remains constant when considering turn delays (Figure 4b). Only with high travel demands do networks in Figure 4(b) show higher travel times. These findings are as expected; however, they provide a foundation for evaluations in Sections 4.2 and 4.3 and subsequent argumentation and implications for final grammar definition.

4.1 Intersection type choice at isolated intersections

This section refers to intersection type choice from a transport perspective, focusing on turn delays in car networks. Isolated intersections are evaluated, detached initially from remaining networks. Consideration of an isolated intersection is a major simplification, which will be corrected in the consecutive section. However, evaluation of isolated intersections already reveals important intersection characteristics, as well as potential consequences for network design.

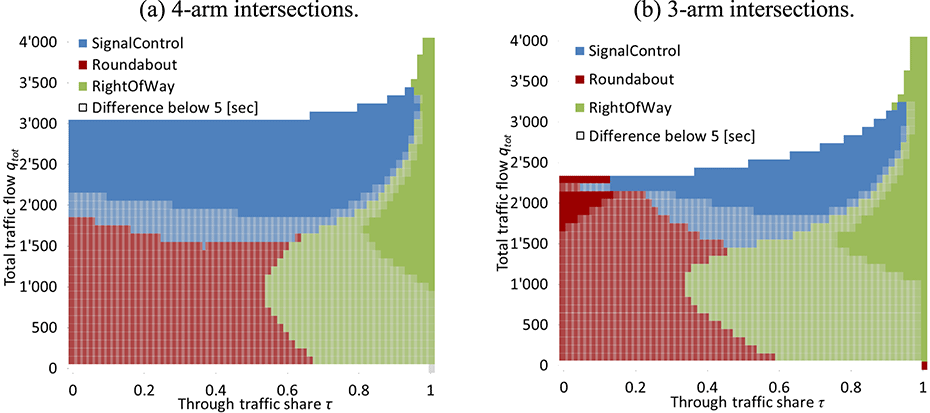
In the following evaluations, turn delays are calculated for roundabouts, signal lights and right-of-way intersections, each with their distinct characteristics. All turn delays are examined under various through traffic shares (as defined in Section 3.1). Figure 5 shows through traffic share $\unicode[STIX]{x1D70F}$ on a designated through traffic direction. Figure 5 highlights intersection types with lowest total turn delays under identical turning flows, as a function of $\unicode[STIX]{x1D70F}$ and total flows $q_{tot}=\unicode[STIX]{x1D6F4}_{n}q_{n}$ . An upper bound of 90 [sec] limits very long turn delays, which would often result in complex queue spillover effects. Intersection types with delay time differences of less than 5 [sec] are displayed in brighter colors. Delays are calculated following Transportation Research Board (2010).

Figure 4. Monetized travel time $c_{tt}$ [SFr./pers.] depending on network density $d_{r}$ at different demand levels (2’000–13’000 [veh./h]) based on $1\times 1$ [ $\text{km}^{2}$ ] networks.

Figure 5 shows slightly lower total turn delays at equally distributed turning flows for roundabouts at low total flows ( ${<}$ 1’500 [veh./h]). Right-of-way intersections have lower turn delays at asymmetric turn flows, due to minor delays for through traffic axes. Signals have higher delays at total flows ${<}$ 1’500 [veh./h]. At moderate flow volumes ( ${\sim}$ 1’500 [veh./h] $-$ 2’000 [veh./h]), there is a shift in minimum delay from roundabouts/right-of-way controlled intersections to signalized intersections.

3-arm intersections differ from 4-arm intersections at high flows ( ${>}$ 2’000 [veh./h]). At 3-arm intersections, roundabouts have low total turn delays at equally distributed turning flows. Signalized intersections have lower turn delays at more asymmetrically distributed turning flows. At very high $\unicode[STIX]{x1D70F}$ values, right-of-way intersections result in lowest delays, which is plausible due to priority rules.

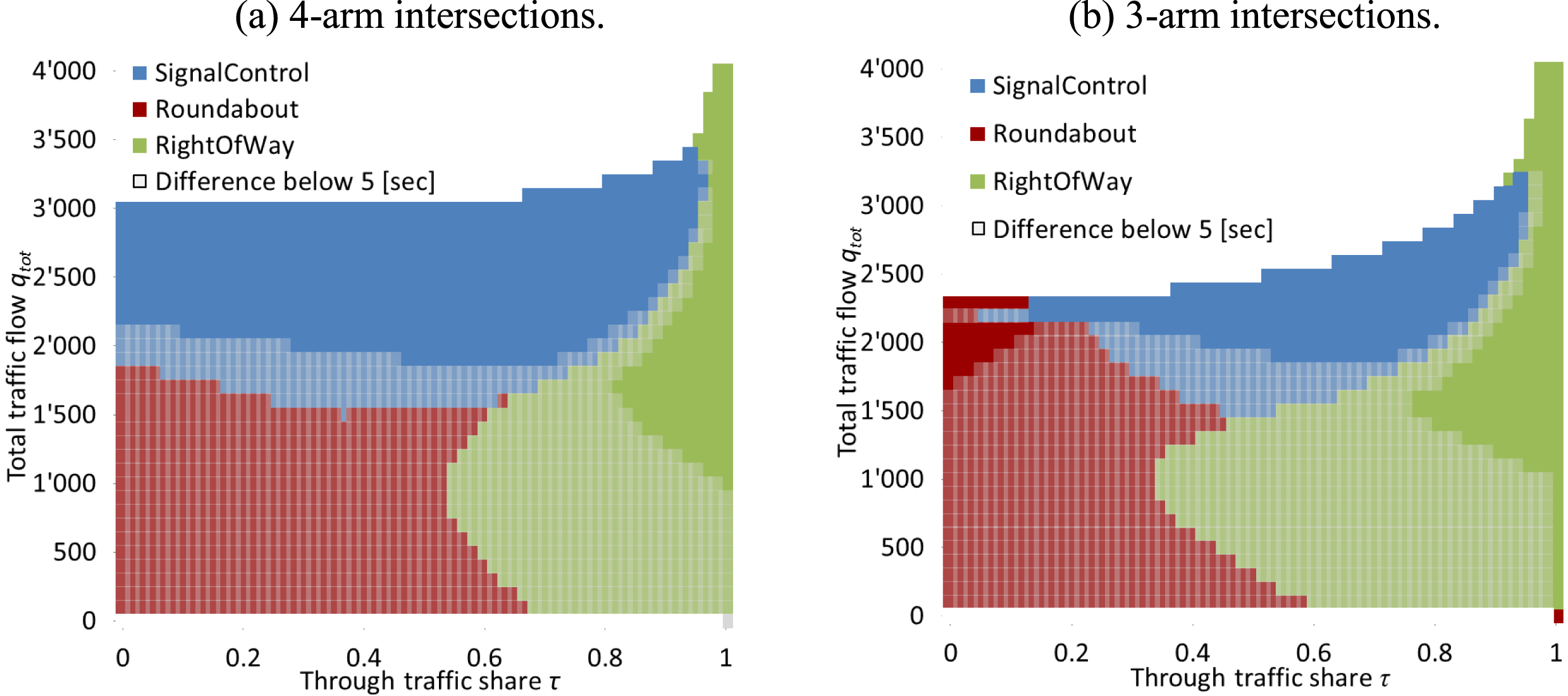
Figure 5. Intersection type choice based on the lowest total turn delays, through traffic share $\unicode[STIX]{x1D70F}$ (defined in Section 3.1) and total traffic flow.

At 4-arm intersections under high flows ( ${>}$ 2’000 [veh./h]), signalized intersections have lowest delays for $\unicode[STIX]{x1D70F}<0.9$ . Phase allocation at signals is more efficient at 4-arm intersections; therefore, higher flows can be accommodated compared to 3-arm intersections. Similar to 3-arm intersections, right-of-way intersections achieve lowest delays at high $\unicode[STIX]{x1D70F}$ values.

Overall, certain intersection types are more efficient for turn delays than others, as a function of number of arms and flows. However, recommendation of intersection type choice requires additional evaluation, especially with the surrounding network design, as discussed in the following section.

4.2 Intersection type choice in adaptive networks

Different intersection types are defined within entire networks in the following, determining their effects. Then, the network design algorithm IACGA optimizes and evaluates transport networks according to a given economic measure (Section 3.5). Network designs with different characteristics emerge during this procedure. The network design algorithm IACGA allows for network topology designs, which go beyond uniform rigid patterns, enabling designs of more generic, but still optimized networks. Study design 1 (Section 2.2.1) is applied in the following evaluation. In this process, one distinct intersection type is considered within a network; an overall comparison between resulting networks is conducted afterward.

Different fixed and distinct network patterns are defined first, serving as benchmark networks to further compare results of the optimized network design. Four of the network patterns are proposed for comparison, based on oblong, or square block shapes. Figure 6 visualizes these distinct patterns, which differ in number of arms at intersections, road densities and different intersection densities. Offset grid (Figure 6d) resembles H-alley and T-alley layouts seen in American Planning Association (2006).

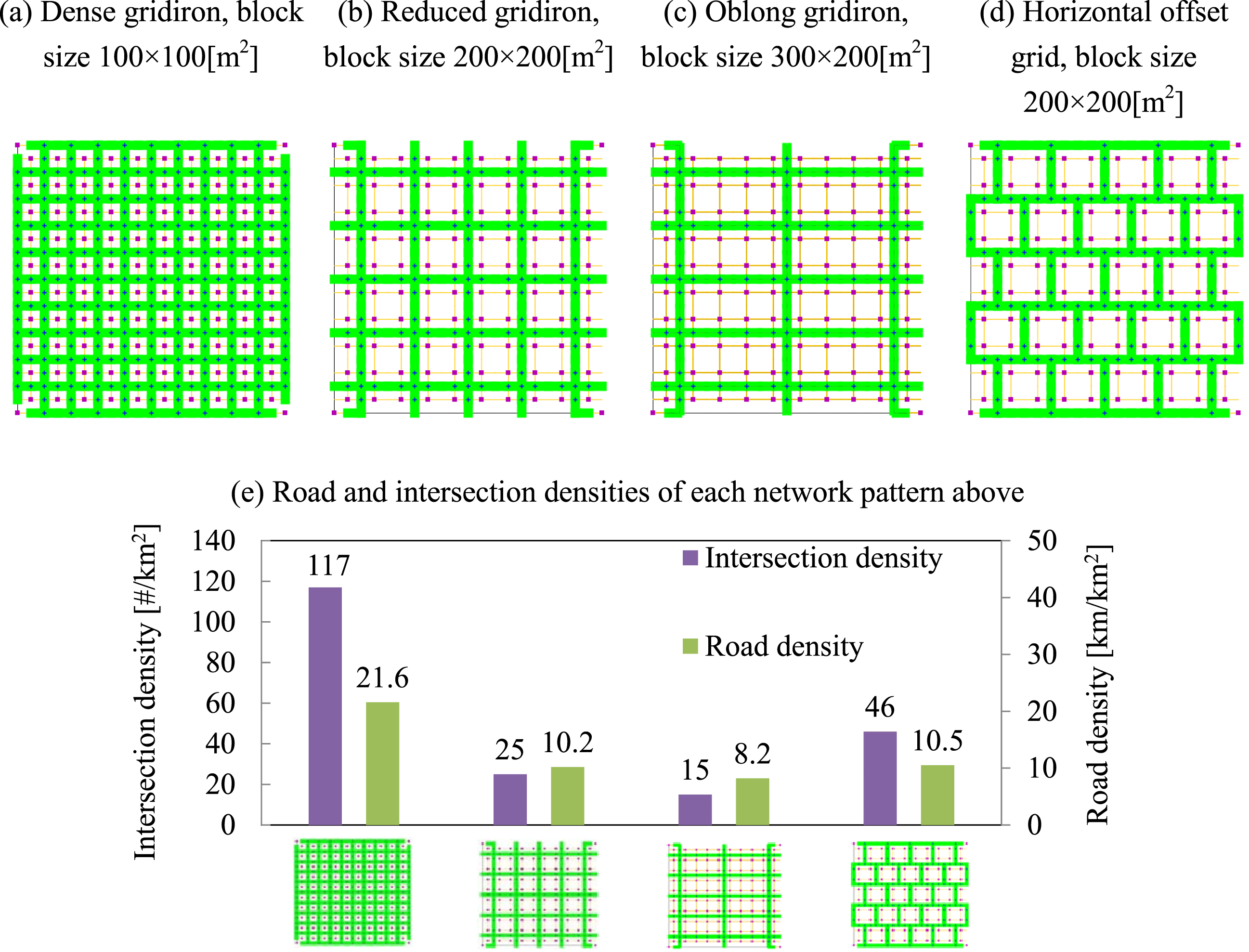
Figure 6. Four comparison network patterns ( $1\times 1$ [ $\text{km}^{2}$ ] in size and 104 demand generating blocks).

Figure 7 depicts average monetized travel time ( $c_{tt}$ ) per person of optimized networks with different road density values $d_{r}$ , and comparison networks patterns (see above). Optimized network topologies are designed with the network design algorithm IACGA (Section 3.5); $c_{tt}$ is minimized and evaluated because it is the major influential component in most cost-benefit analyses, as well as for infrastructure cost alone. It is assumed that road density $d_{r}$ is proportional to monetary infrastructure costs, allowing final evaluation of $d_{r}$ as a major infrastructure cost related variable, important because monetary infrastructure costs are a major economic uncertainty. Travel demand is determined according to densities $d_{pop}$ and $d_{jobs}$ (see Section 4.4 below, where these values are relaxed in sensitivity analysis.). Due to IACGA’s heuristic nature (Section 3.5), final network densities can vary; therefore, optimized networks are not continuously spread over $d_{r}$ . Figure 7 focuses on comparison between reference patterns and optimized networks with similar infrastructure costs. X axis is in [km/km $^{2}$ ] and mirrors road infrastructure costs. Three reference patterns (defined in Figures 6(b)–(d)) are added in Figure 7 for comparison (the pattern in Figure 6(a) has very high road densities in comparison and is therefore ignored).

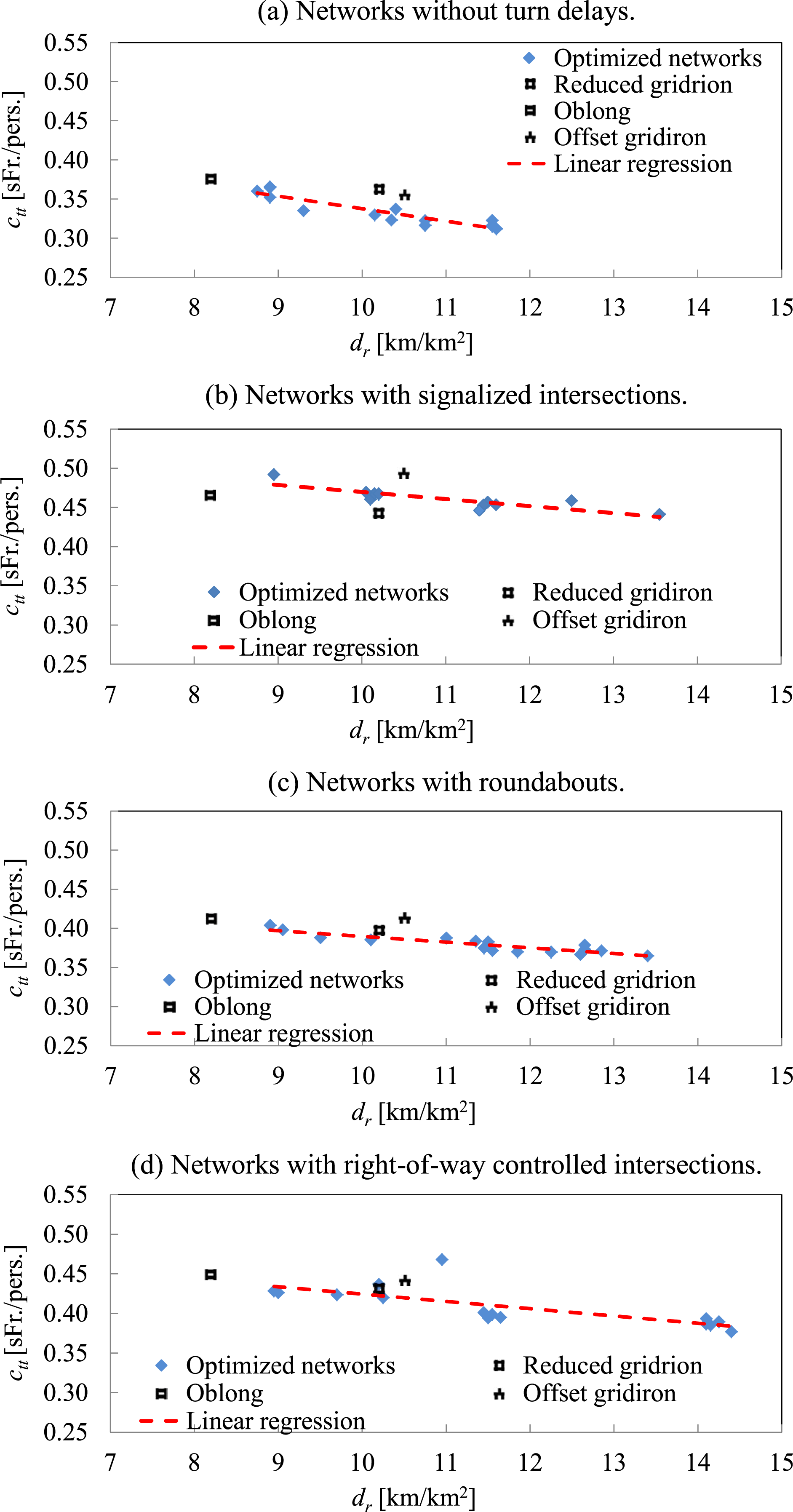
Figure 7. Comparison of optimized networks and comparison reference patterns in relation to average generalized costs $c_{tt}$ [SFr./pers.].

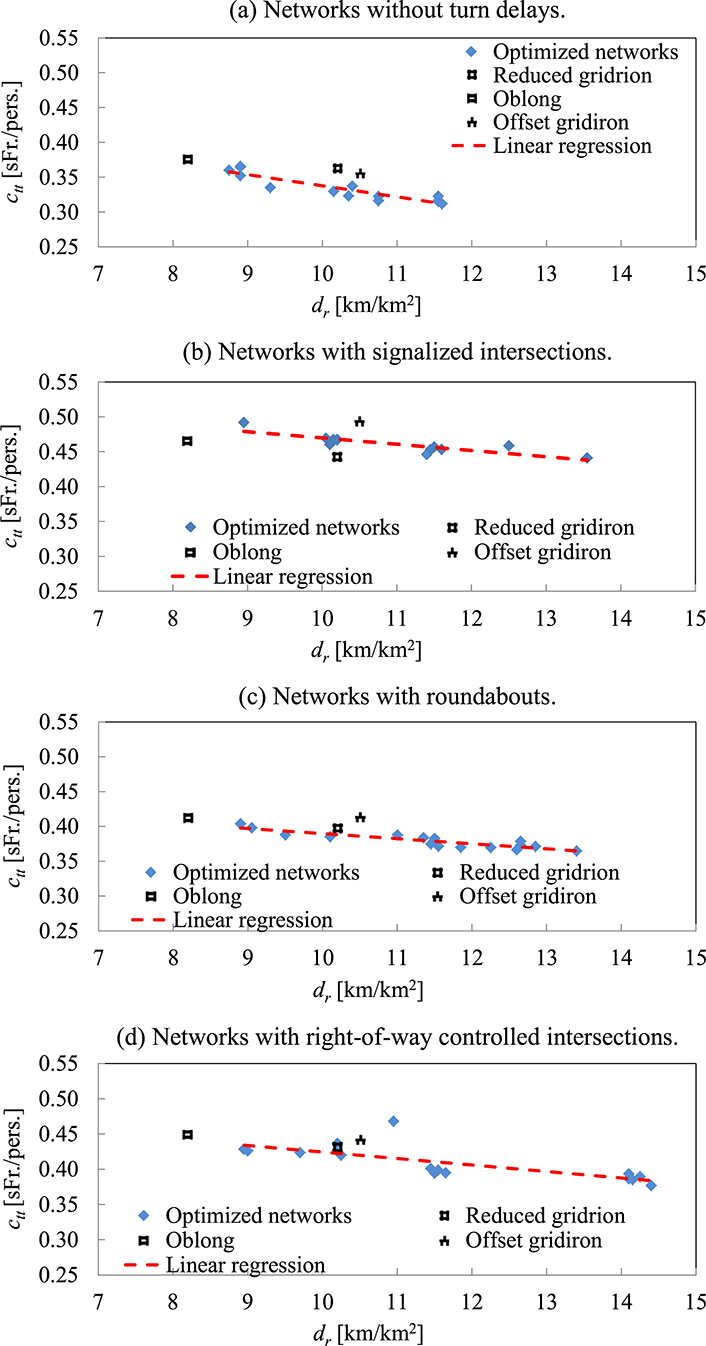
Results visualized in Figure 7(a) ignore turn delay influences, unlike Figure 7(b)–(d), which include turn delays. For certain transport modes and networks, ignoring turn delays might still be reasonable, especially for low-speed transport modes, such as pedestrians. Subjects in modes with low speeds travel longer on edges relative to waiting time at intersections (e.g. pedestrian or bicycles). In these cases, adding edges decreases travel cost. Therefore, the slope of the fitted regression line is steeper, compared to the following Figures 7(b)–(d).

Figure 7(b) displays average $c_{tt}$ values of optimized networks and comparison patterns, both with implemented signalized intersections. Results show that signalized intersections produce especially low turn delays in gridiron networks with relatively low intersection densities. Minimum average delays at signals (due to phases) favor networks with lower intersection densities. Gridirons are particularly efficient due to more efficient phase allocation at 4-arm intersections, compared to 3-arm intersections. These results support findings above (Section 4.1).

Figure 7(c) visualizes $c_{tt}$ values of comparison patterns and optimized networks with roundabouts. Comparison patterns result in similar costs compared to optimized patterns. Figure 7(d) depicts costs of optimized networks for right-of-way intersections, which are slightly lower than costs of the comparison patterns. Overall, Figure 7 shows that networks with right-of-way intersections and roundabouts have lower $c_{tt}$ values compared to signals based on a relatively low travel demand, which is in line with the results above.

Linear regression is applied to define marginal generalized cost savings $\unicode[STIX]{x1D6FF}c/\unicode[STIX]{x1D6FF}d$ and elasticities $\unicode[STIX]{x1D6FF}c/\unicode[STIX]{x1D6FF}d\cdot \bar{l}/\bar{c}$ of optimized networks (Section 2.3.1). Network length $l$ is proportional to density $d_{r}$ due to identical area size. Regression linearity is assumed as an approximation. The first line in Table 3 refers to marginal generalized cost savings as they relate to road network length. The second line shows elasticity values for different networks as a function of different intersection types. Marginal generalized cost savings and elasticities differ considerably between intersection types. Right-of-way intersections have highest elasticity values and relatively high marginal cost values. Adding road length on networks with embedded right-of-way intersections increases generalized cost savings more than when adding roads in networks with signals. However, at signalized intersections and roundabouts, increasing capacity on existing roads might reduce user cost more than additional road length, as evaluated further in Section 4.4.

Table 3. Estimated marginal generalized cost savings and elasticity values for network length $l$ for different intersection types

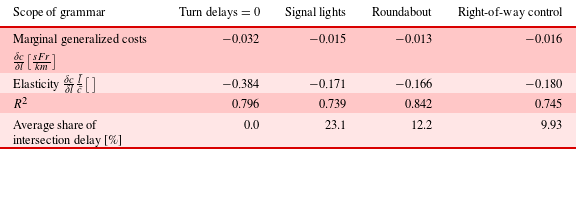
4.3 Network topology

Unlike the examined intersection types, network topologies have diverse, often unclear characteristics; numerous different network topologies can be found in existing networks that challenge topology evaluation and recommendation. Therefore, key measures are suggested to emphasize major topology characteristics. Topologies of optimized networks are evaluated and compared with each other and with the topologies of the comparison network patterns. Evaluation takes place with study design 2, which compares outcomes of optimization processes (Section 2.2.2).

Table 4. Characteristics of example networks ( $1\times 1$ [ $\text{mile}^{2}$ ]), and optimized networks

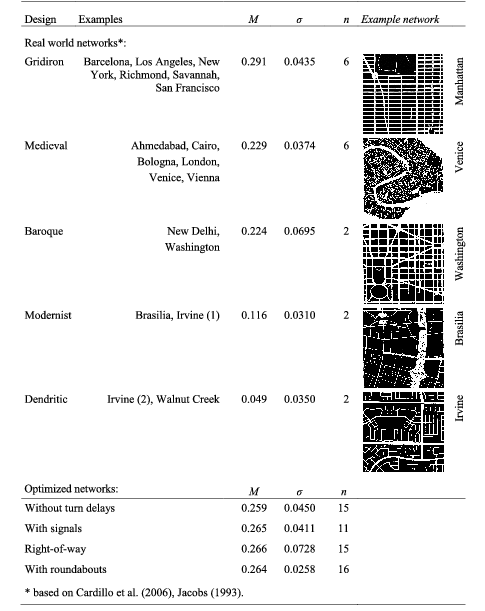
Meshedness $M$ is an important measurement in topology evaluation (Section 3.1); Table 4 summarizes meshedness values. The upper half of Table 4 shows $M$ values for multiple real-world network patterns (Cardillo et al. 2006), including the number of evaluated networks $n$ . $M$ differs considerably between reference patterns. Networks in New York, Savannah, and San Francisco have values of $M>0.3$ , while Irvine and Walnut Creek have $M<0.1$ . The lower half of Table 4 shows $M$ values for optimized networks designed with different urban densities, resulting in infrastructure costs and optimized for low generalized user costs. Despite different intersection types, high $M$ values are achieved through optimization processes, including low standard deviation $\unicode[STIX]{x1D70E}$ . There is evidence that networks with high $M$ values correlate with low user costs. A graph-based efficiency analysis showed similar results for real-world networks (Cardillo et al. 2006). Still, it is not yet clear whether $M$ contributes to high efficiency; thus, more evaluations were conducted with additional variables, shown below. Importantly, travel demand patterns and road capacity assumptions, which were assumed constant in the above evaluations, are relaxed in the following.

4.4 Urban density sensitivity and reliability

In initial planning stages, planners are faced with unknowns about future population and workplace densities, making it interesting to analyze how much urban density one network can support without unacceptable travel time increase ( $\unicode[STIX]{x1D6E5}t^{x\%}$ ), as proposed in Section 2.3.2 in the Maximum Network Supply Method. An upper bound is assumed for accepted travel time changes ( $+$ 20% in the following $\rightarrow$ $\unicode[STIX]{x1D6E5}t^{20\%}$ ), which is achieved by gradually increasing densities of population and jobs ( $d_{pop}$ and $d_{jobs}$ ). The goal is to determine how much we can proportionally increase $d_{pop}$ and $d_{jobs}$ in a given area without unacceptable increase in travel time ( $\unicode[STIX]{x1D6E5}d_{pop,jobs}$ ( $\unicode[STIX]{x1D6E5}t^{x\%}$ )). 38 optimized networks are evaluated in a stepwise linear regression with eight independent, topology-related variables: network density, dead-end density, 3- and 4-arm intersection density, meshedness, face density and circumference, intersection density and multiple intersection types. Proposed statistical evaluation is able to overcome at least some constraints seen the initial network definition. Table 5 shows corresponding regression results. Table 1 specifies 3 scenarios with different capacity standards, which are also considered in Table 5; scenario 0 has default capacities, scenario 1 and scenario 2 have increasing road and intersection capacities, respectively.

Table 5. Regression result of optimized networks for $\unicode[STIX]{x1D6E5}d_{pop,jobs}$ ( $\unicode[STIX]{x1D6E5}t^{20\%}$ ) as a dependent variable, differentiated in given scenarios (Table 1)

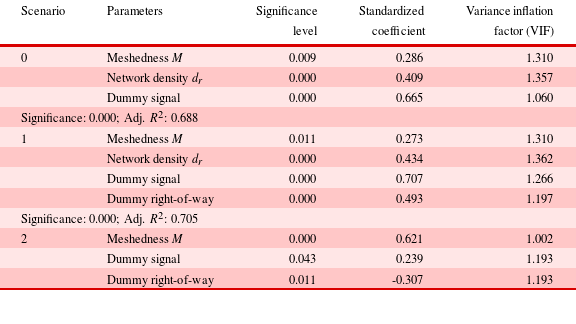
Significance: 0.000; Adj. $R^{2}$ : 0.586

In Table 5, $d_{r}$ and $M$ contribute significantly to $\unicode[STIX]{x1D6E5}d_{pop,jobs}$ ( $\unicode[STIX]{x1D6E5}t^{20\%}$ ) in scenarios 0 and 1. Low multicollinearity results between $d_{r}$ and $M$ . Signal implementation is also significant, due to lower delays at high flows (Figure 5). Right-of-way intersections only have a positive significant influence in scenario 1, but less than signals. The positive influence of right-of-way intersections and signals suggests that roundabouts might have higher delays at increasing densities. In scenario 2, right-of-way intersections have a negative influence, indicating that capacities of right-of-way intersections cannot increase as much as roundabout and signal capacities. Right-of-way intersections are thus less efficient with additional lanes and increasing flows.

Table 5 shows significant values for $M$ , signal and right-of-way in scenario 2. Additionally, $d_{r}$ is significant even after a stepwise linear regression. However, standardized $\unicode[STIX]{x1D6FD}$ value of $d_{r}$ is negative in combination with $M$ , which seems unreasonable. $M$ and $d_{r}$ correlate slightly, as seen already in scenarios 0 and 1. Therefore, $d_{r}$ is excluded in scenario 2 because of low standardized $\unicode[STIX]{x1D6FD}$ and lower significance compared to $M$ .

5 Grammar extraction

Grammars can be formulated in many different ways. Many geometry-based (shape) grammars are visualized directly in geometric plans, e.g. Stiny & Mitchell (1978). While geometry-based approaches would be more straightforward, descriptive approaches allow for grammar complexity and application specifications. Urban design complexity and interdependences of grammars particularly hamper a straightforward geometric rule description. Absolute geometric lengths and angles might vary; e.g. meshedness cannot be characterized with absolute lengths. Therefore, a formal definition combined with a description is proposed here.

This paper defines a subset for urban network grammars, extracted from the above findings and constraints. Proposed grammars in Table 6 refer to travel cost efficiency as an application specification ( $s_{7}$ ). In Table 6, $r_{1}$ and $s_{1}$ correspond to each other because they are stated next to each other in the same line. Additionally, $s_{7}$ corresponds to $r_{1}-r_{6}$ , and $s_{8}$ corresponds to $r_{3}-r_{6}$ . Grammars can then be derived directly from Table 6, e.g. $g_{1}(r_{1},\{s_{1},s_{7}\}),\ldots ,g_{6}(r_{6},\{s_{6},s_{7},s_{8}\})$ .

Table 6. Extracted grammars for transport network design

5.1 Network topology

The following recommendations aim at efficient network topologies with low travel times and generalized travel costs:

Grammar 1:

Based on all evaluations, $M>0.2$ is a practical option for efficient networks, independent of flows and intersection types. This rule is also valid for different modes of different travel speeds.

Grammar 2:

Low dead-end density is recommended for efficient networks, independent of flows and intersection types. This rule is also valid for different modes with different speeds.

Grammar 3:

Higher network road density $d_{r}$ improves network efficiency until a certain threshold due to increasing turn delays. Exceptions are networks for modes with low turn delays, e.g. pedestrian networks (leading to dense networks with low path capacities).

5.2 Intersection type choice

Grammar 4:

Signals are more efficient for increasing urban densities and travel flows. However, signals have relatively high turn delays at low flows, leading to higher travel times. Therefore, at lower flows, roundabouts are recommended at equally distributed flows and right-of-way intersections at high through traffic shares.

Grammar 5:

Gridirons and oblong patterns have low travel times at high flows.

Grammar 6:

Signals have lower turn delays at 4-arm intersections. Therefore, overall travel delay is low for a combination of gridiron networks with signals at high flows.

5.3 Interpretation and comparison of gained results

Overall, results showed that fundamental travel mode characteristics and flow influence network design, including speed, capacity, queuing and the general space usage while traveling. This means that network design is derived from given travel mode characteristics and urban density, such as driving speed and intersection behavior and queuing. In general, network design for any type of transportation mode is a function of its mode characteristics, valid not only for existing modes and technologies, but also future modes with new technologies. The resulting dependencies are stated as a set of detailed grammar.

Results mirror real-world networks described in Section 1 and listed in Table 4. High meshedness $(g_{1}(r_{1},\{s_{1},s_{7}\}))$ is found in practically all networks except treelike networks, which underperform given considered economic criteria; similar results are found for low dead-end density ( $g_{2}$ ). High network density ( $g_{3}$ ) is only efficient for certain modes, but for car networks, an upper limit is effective and is proposed for efficiency reasons. This result is similar to real-world developments, were cars are excluded from certain inner city areas due to capacity issues (e.g. Bausells (2016). Intersection type choice ( $g_{4}$ ) is similar to observations in residential neighborhoods with low volumes and right-of-way intersections, compared to arterials with signal crossings for higher capacities (similar to HCM; Transportation Research Board 2010). Regarding rectangular intersection arms layout, Strano et al. (2012) found a shift toward oblong and square parcel shape in empirical data and increasing 4-arm intersection density, similar to $g_{5}$ . In parallel, signals remain functional at 4-arm intersections, as suggested in $g_{6}$ and observed in real-world networks.

Three design limitations are stated considering network design (Section 1.3): (1) the required generalized cost optimization in network design, (2) capacity limitation of any current transport networks and (3) variable and unpredictable travel demand forecast and fluctuation. Proposed methodologies tackle all limitations to a certain extent. Generalized cost optimization (design limitation 1) is covered with the proposed study designs (Section 2.2 and 2.3.1), where only optimized networks are designed and statistically evaluated. Corresponding results are listed in Sections 4.2 and 4.3. Limitation 2 refers to limited capacities and existing networks and transportation infrastructure. For transformation of existing networks, grammar rules are able to consider transformation from available infrastructure to new infrastructure. Section 5.4 also proposes a transition between modes. For new networks, topology and intersection type choice are recommended for car networks with minimum network density (elasticity approach, Sections 4.1, 4.2, 4.4), and derived for other modes (Section 5.4). Limitation 3 refers to fluctuation in future travel demand and uncertainty. Section 2.3.2 proposed the new Maximum Network Supply Method, which is successfully applied in Section 4.4, where travel demand uncertainty is addressed.

5.4 Topology design conflicts

Travel time, speed and turn delays depend on network topology, intersection types and densities. Slow modes, e.g. pedestrians, spend relatively less time at intersections than on edges. As evaluations showed, increasing road density provides higher travel time savings for modes with low turn delays. Slow modes can benefit most from a dense network topology, higher intersection densities and even higher 3-arm intersection shares. The situation changes when considering faster modes, e.g. cars, and higher relative turn delays. Especially in dense urban areas, fast modes with higher turn delay shares profit from lower intersection densities and high road and intersection capacities and higher 4-arm intersection shares. Similar findings hold for transit networks; dense bus networks with short headways and changing times contrast with long-distance networks, longer headways and stopover times. In summary, modes with varying travel speeds require different network topologies with different densities; this has fundamental consequences for optimal transport network design.

Grid and block size specifications are important; hence, just a ‘gridiron’ pattern recommendation is insufficient. The above findings reveal that dense networks, including 3- and 4-arm intersections, are suitable for transport modes with lower turn delay shares. However, less dense road networks combined with 4-arm intersections and lower intersection densities are recommended for transport modes with high turn delay shares (e.g. cars and signals). These findings are somewhat contradictory, but do indicate lower general travel costs due to overall lower turn delays; importantly, they also significantly impact network design and network transformation as a result of changing usage. Transformation of road networks with increasing urban densities is often necessary due to increasing travel demand and flows. Changing network densities or shifting from one mode to another is the biggest challenge, as seen in historical transport developments. Growing urban systems must be redesigned over time as densities increase, travel modes change and new needs emerge. In a classic example, medieval cities were designed for pedestrians, while gridirons are more suitable for carriages, buses, tramways and motorway grid overlays for cars. Grammars can support this transition by (1) providing sufficient generic and adaptive rules for potential changes and (2) providing information about the effects of potential rule implementations.

6 Conclusion and outlook

A novel methodological framework is successfully proposed and executed for network design grammar evaluation and grammars are quantitatively evaluated with an elasticity measure and a novel Maximum Network Supply Method. Grammars are defined and evaluated for road network topology and intersection type choice, including sensitivity analysis on both demand and supply sides. For future applications, this new knowledge about grammars can be implemented for transport mode changes, e.g. when new technologies will enable faster travel with fewer turn delays.

Proposed network design conflict breaks ongoing network design challenges down to transport mode specifications and requirements; e.g. cars have higher turn delay shares in urban areas than pedestrians, thus requiring specific network characteristics. Potential solutions for future transport modes with different requirements are outside the scope of this research. Alexander et al. (1977) show a possible straightforward solution by cutting down network length and avoiding rat running, discussed in cities such as Barcelona (Bausells 2016). When considering sufficient road capacity and low turn delays on through streets, closing them down can maintain network performance, as results showed. Here, we refer to planning limitation 3 (Introduction) and potential transformation processes. Additional detail is needed about factors like queue spillover effects for cars or public transport modes.