Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-18T10:44:09.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Volume function and Mahler measure of exact polynomials

Part of: Polynomials and matrices

Published online by Cambridge University Press:  14 April 2021

Antonin Guilloux  and
Julien Marché
Antonin Guilloux
Affiliation:
Sorbonne Université, CNRS, IMJ-PRG and INRIA OURAGAN, 75252Paris cédex 05, [email protected]
Julien Marché
Affiliation:
Sorbonne Université, CNRS, IMJ-PRG, 75252Paris cédex 05, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a class of two-variable polynomials called exact polynomials which contains 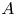$A$-polynomials of knot complements. The Mahler measure of these polynomials can be computed in terms of a volume function defined on the vanishing set of the polynomial. We prove that the local extrema of the volume function are on the two-dimensional torus and give a closed formula for the Mahler measure in terms of these extremal values. This formula shows that the Mahler measure of an irreducible and exact polynomial divided by 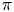$\pi$ is greater than the amplitude of the volume function. We also prove a K-theoretic criterion for a polynomial to be a factor of an 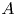$A$-polynomial and give a topological interpretation of its Mahler measure.

Keywords

Mahler measureA-polynomialamoebaK-theoryhyperbolic geometry

MSC classification

Primary: 11C08: Polynomials
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 4 , April 2021 , pp. 809 - 834
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertin, M.-J. and Lalín, M., Mahler measure of multivariable polynomials, in Women in numbers 2: research directions in number theory, Contemporary Mathematics, vol. 606 (American Mathematical Society, Providence, RI, 2013), 125–147.CrossRefGoogle Scholar
Boyd, D. W., Mahler's measure and invariants of hyperbolic manifolds, in Number theory for the millennium, I (Urbana, IL, 2000) (A. K. Peters, Natick, MA, 2002), 127–143.Google Scholar
Boyd, D. W. and Rodriguez-Villegas, F., Mahler's measure and the dilogarithm. I, Canad. J. Math. 54 (2002), 468–492.CrossRefGoogle Scholar
Boyd, D. W., Rodriguez-Villegas, F. and Dunfield, N. M., Mahler's measure and the dilogarithm (II). Preprint (2005), arXiv:math/0308041v2.Google Scholar
Brunault, F. and Neururer, M., Mahler measures of elliptic modular surfaces, Trans. Amer. Math. Soc. 372 (2019), 119–152.CrossRefGoogle Scholar
Cooper, D., Culler, M., Gillet, H., Long, D. D. and Shalen, P. B., Plane curves associated to character varieties of $3$-manifolds, Invent. Math. 118 (1994), 47–84.CrossRefGoogle Scholar
Culler, M. and Dunfield, N. M., Pe: a tool for studying pe character varieties and extension loci, https://bitbucket.org/t3m/pe (15/12/2017).Google Scholar
Culler, M., Dunfield, N. M., Goerner, M. and Weeks, J. R., SnapPy, a computer program for studying the geometry and topology of 3-manifolds, http://snappy.computop.org (01/09/2017).Google Scholar
Deninger, C., Deligne periods of mixed motives, $K$-theory and the entropy of certain $\textbf {Z}^{n}$-actions, J. Amer. Math. Soc. 10 (1997), 259–281.CrossRefGoogle Scholar
Dunfield, N. M., Cyclic surgery, degrees of maps of character curves, and volume rigidity for hyperbolic manifolds, Invent. Math. 136 (1999), 623–657.CrossRefGoogle Scholar
Dunfield, N. M., Examples of non-trivial roots of unity at ideal points of hyperbolic $3$-manifolds, Topology 38 (1999), 457–465.CrossRefGoogle Scholar
Francaviglia, S., Hyperbolic volume of representations of fundamental groups of cusped $3$-manifolds, Int. Math. Res. Not. IMRN 9 (2004), 425–459.CrossRefGoogle Scholar
Francaviglia, S. and Savini, A., Volume rigidity at ideal points of the character variety of hyperbolic 3-manifolds, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 20 (2020), 1325–1344.Google Scholar
Hutchinson, K., The second homology of ${\rm SL_2}$ of $S$-integers, J. Number Theory 159 (2016), 223–272.CrossRefGoogle Scholar
Lalín, M. N., Some examples of Mahler measures as multiple polylogarithms, J. Number Theory 103 (2003), 85–108.CrossRefGoogle Scholar
Liechti, L. and Marché, J., Overcommuting pairs in groups and 3-manifolds bounding them, J. Lond. Math. Soc. (2), to appear. Preprint (2019), arXiv:1903.11418.Google Scholar
Lê, T. T. Q. and Zhang, X., Character varieties, $A$-polynomials and the AJ conjecture, Algebr. Geom. Topol. 17 (2017), 157–188.CrossRefGoogle Scholar
Maillot, V., Géométrie d'Arakelov des variétés toriques et fibrés en droites intégrables, Mém. Soc. Math. Fr. (N.S.) 80 (2000).Google Scholar
Mikhalkin, G., Real algebraic curves, the moment map and amoebas, Ann. of Math. (2) 151 (2000), 309–326.CrossRefGoogle Scholar
Marché, J. and Maurin, G., Singular intersections of subgroups and character varieties, to appear. Preprint (2014), arXiv:1406.2862.Google Scholar
Rodriguez-Villegas, F., Modular Mahler measures. I, in Topics in number theory (University Park, PA, 1997), Mathematics and its Applications, vol. 467 (Kluwer Academic, Dordrecht, 1999), 17–48.Google Scholar
Sage Developers, SageMath, the Sage Mathematics Software System (Version 8.1) (2017), http://www.sagemath.org.Google Scholar
Smyth, C. J., On measures of polynomials in several variables, Bull. Aust. Math. Soc. 23 (1981), 49–63.CrossRefGoogle Scholar
Verschelde, J., Algorithm 795: PHCpack: a general-purpose solver for polynomial systems by homotopy continuation, ACM Trans. Math. Software 25 (1999), 251–276.CrossRefGoogle Scholar
Weibel, C. A., The K-book: an introduction to algebraic K-theory, Graduate Studies in Mathematics, vol. 145 (American Mathematical Society, Providence, RI, 2013).Google Scholar