Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-01T08:42:44.342Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal polynomials for singular curves on surfaces

Part of: Projective and enumerative geometry Curves Cycles and subschemes

Published online by Cambridge University Press:  06 June 2014

Jun Li  and
Yu-jong Tzeng
Jun Li
Affiliation:
Department of Mathematics, Stanford University, California, CA 94305, USA email [email protected]
Yu-jong Tzeng
Affiliation:
Department of Mathematics, Harvard University, Cambridge, MA 02138, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 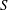$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$ be a complex smooth projective surface and 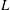$L$ be a line bundle on 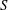$S$. For any given collection of isolated topological or analytic singularity types, we show the number of curves in the linear system 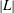$|L|$ with prescribed singularities is a universal polynomial of Chern numbers of 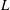$L$ and 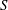$S$, assuming 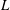$L$ is sufficiently ample. More generally, we show for vector bundles of any rank and smooth varieties of any dimension, similar universal polynomials also exist and equal the number of singular subvarieties cutting out by sections of the vector bundle. This work is a generalization of Göttsche’s conjecture.

Keywords

curve countinguniversal polynomialGöttsche’s conjecture

MSC classification

Secondary: 14N10: Enumerative problems (combinatorial problems) 14C20: Divisors, linear systems, invertible sheaves 14H20: Singularities, local rings
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 7 , July 2014 , pp. 1169 - 1182
Copyright
© The Author(s) 2014 

References

Bryan, J. and Leung, N. C., The enumerative geometry of K3 surfaces and modular forms, J. Amer. Math. Soc. 13 (2000), 371–410.Google Scholar
Caporaso, L. and Harris, J., Counting plane curves of any genus, Invent. Math. 131 (1998), 345–392.Google Scholar
Fulton, W., Intersection theory, 2nd edition (Springer, Berlin, 1998).Google Scholar
Göttsche, L., A conjectural generating function for numbers of curves on surfaces, Comm. Math. Phys. 196 (1998), 523–533.Google Scholar
Greuel, G. M., Lossen, C. and Shustin, E., Introduction to singularities and deformations (Springer, 2007).Google Scholar
Harris, J., On the Severi problem, Invent. Math. 84 (1986), 445–461.Google Scholar
Harris, J. and Pandharipande, R., Severi degrees in cogenus 3, Preprint (1995),arXiv:alg-geom/9504003.Google Scholar
Kazarian, M. E., Multisingularities, cobordisms, and enumerative geometry, Russian Math. Surveys 58 (2003), 665.Google Scholar
Kemeny, M., The universal severi variety of rational curves on k3 surfaces, Bull. Lond. Math. Soc. 45 (2013), 159–174.Google Scholar
Kerner, D., Enumeration of singular algebraic curves, Israel J. Math. 155 (2006), 1–56.Google Scholar
Kleiman, S. and Piene, R., Enumerating singular curves on surfaces, Contemp. Math. 241 (1999), 209–238.Google Scholar
Kool, M., Shende, V. and Thomas, R., A short proof of the Göttsche conjecture, Geom. Topol. 15 (2011), 397–406.Google Scholar
Lee, Y. P. and Pandharipande, R., Algebraic cobordism of bundles on varieties, J. Eur. Math. Soc. 14 (2012), 1081–1101.Google Scholar
Levine, M. and Pandharipande, R., Algebraic cobordism revisited, Invent. Math. 176 (2009), 63–130.Google Scholar
Li, J. and Wu, B., Good degeneration of quot-schemes and coherent systems, Preprint (2011),arXiv:1110.0390.Google Scholar
Liu, A. K., Family blowup formula, admissible graphs and the enumeration of singular curves, I, J. Differential Geom. 56 (2000), 381–579.CrossRefGoogle Scholar
Liu, A. K., The algebraic proof of the universality theorem, Preprint (2004),arXiv:math/0402045.Google Scholar
Qviller, N., Structure of node polynomials for curves on surfaces, Preprint (2011),arXiv:1102.2092.Google Scholar
Rennemo, J. V., Universal polynomials for tautological integrals on Hilbert schemes, Preprint (2012), arXiv:1205.1851.Google Scholar
Tzeng, Y., A proof of the Göttsche–Yau–Zaslow formula, J. Differential Geom. 90 (2012), 439–472.Google Scholar
Vainsencher, I., Enumeration of n-fold tangent hyperplanes to a surface, J. Algebraic Geom. 4 (1995), 503–526.Google Scholar
Vainsencher, I., Hypersurfaces with up to six double points, Comm. Algebra 31 (2003), 4107–4129.Google Scholar
Vakil, R., Counting curves on rational surfaces, Manuscripta Math. 102 (2000), 53–84.Google Scholar