Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T04:25:25.557Z Has data issue: false hasContentIssue false
  • English
  • Français

A uniform treatment of Grothendieck's localization problem

Part of: Local theory Topological rings and modules General commutative ring theory Local rings and semilocal rings Arithmetic rings and other special rings

Published online by Cambridge University Press:  24 January 2022

Takumi Murayama
Takumi Murayama*
Affiliation:
Department of Mathematics, Princeton University, Fine Hall, Washington Road, Princeton, NJ 08544-1000, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $f\colon Y \to X$ be a proper flat morphism of locally noetherian schemes. Then the locus in 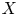$X$ over which 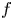$f$ is smooth is stable under generization. We prove that, under suitable assumptions on the formal fibers of $X$, the same property holds for other local properties of morphisms, even if 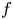$f$ is only closed and flat. Our proof of this statement reduces to a purely local question known as Grothendieck's localization problem. To answer Grothendieck's problem, we provide a general framework that gives a uniform treatment of previously known cases of this problem, and also solves this problem in new cases, namely for weak normality, seminormality, $F$-rationality, and the ‘Cohen–Macaulay and 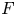$F$-injective’ property. For the weak normality statement, we prove that weak normality always lifts from Cartier divisors. We also solve Grothendieck's localization problem for terminal, canonical, and rational singularities in equal characteristic zero.

Keywords

Grothendieck's localization problemGrothendieck's lifting problemweak local uniformizationP-morphismweak normality

MSC classification

Primary: 14B07: Deformations of singularities
Secondary: 13H10: Special types (Cohen-Macaulay, Gorenstein, Buchsbaum, etc.) 14B25: Local structure of morphisms 13J10: Complete rings, completion 13F45: Seminormal rings 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 1 , January 2022 , pp. 57 - 88
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This material is based upon work supported by the National Science Foundation under Grant Nos. DMS-1701622 and DMS-1902616.

References

André, M., Méthode simpliciale en algèbre homologique et algèbre commutative, Lecture Notes in Mathematics, vol. 32 (Springer, Berlin, 1967); MR 214644.CrossRefGoogle Scholar
André, M., Localisation de la lissité formelle, Manuscripta Math. 13 (1974), 297–307; MR 357403.CrossRefGoogle Scholar
Avramov, L. L., Flat morphisms of complete intersections, Dokl. Akad. Nauk 225 (1975), 11–14, translated from the Russian by D. L. Johnson; MR 396558.Google Scholar
Avramov, L. L., Homology of local flat extensions and complete intersection defects, Math. Ann. 228 (1977), 27–37; MR 485836.CrossRefGoogle Scholar
Avramov, L. L. and Foxby, H.-B., Grothendieck's localization problem, in Commutative algebra: syzygies, multiplicities, and birational algebra (South Hadley, MA, 1992), Contemporary Mathematics, vol. 159 (American Mathematical Society, Providence, RI, 1994), 1–13; MR 1266174.CrossRefGoogle Scholar
Avramov, L. L., Foxby, H.-B. and Herzog, B., Structure of local homomorphisms, J. Algebra 164 (1994), 124–145; MR 1268330.CrossRefGoogle Scholar
Bingener, J. and Flenner, H., On the fibers of analytic mappings, in Complex analysis and geometry, Univ. Ser. Math. (Plenum, New York, 1993), 45–101; MR 1211878.CrossRefGoogle Scholar
Bourbaki, N., Commutative algebra. Chapters 1–7, Elements of Mathematics (Berlin) (Springer, Berlin, 1998), translated from the French, reprint of the 1989 English translation; MR 1727221.Google Scholar
Boutot, J.-F., Singularités rationnelles et quotients par les groupes réductifs, Invent. Math. 88 (1987), 65–68; MR 877006.CrossRefGoogle Scholar
Brezuleanu, A. and Ionescu, C., On the localization theorems and completion of $P$-rings, Rev. Roumaine Math. Pures Appl. 29 (1984), 371–380; MR 758426.Google Scholar
Brezuleanu, A. and Rotthaus, C., Eine Bemerkung über Ringe mit geometrisch normalen formalen Fasern, Arch. Math. (Basel) 39 (1982), 19–27; MR 674529.CrossRefGoogle Scholar
Bruns, W. and Herzog, J., Cohen-Macaulay rings, Cambridge Studies in Advanced Mathematics, vol. 39, revised edition (Cambridge University Press, Cambridge, 1998); MR 1251956.CrossRefGoogle Scholar
Cangemi, M. R. and Imbesi, M., Some problems on $P$-morphisms in codimension and codepth $k$, Stud. Cerc. Mat. 45 (1993), 19–30; MR 1244750.Google Scholar
Chiriacescu, G., On the theory of Japanese rings, Rev. Roumaine Math. Pures Appl. 27 (1982), 945–948; MR 683072.Google Scholar
Cossart, V. and Piltant, O., Resolution of singularities of arithmetical threefolds, J. Algebra 529 (2019), 268–535; MR 3942183.CrossRefGoogle Scholar
de Jong, A. J., Smoothness, semi-stability and alterations, Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93; MR 1423020.CrossRefGoogle Scholar
Datta, R. and Murayama, T., Permanence properties of F-injectivity, Preprint (2020), arXiv:1906.11399v2.Google Scholar
Grothendieck, A. and Dieudonné, J., Eléments de géométrie algébrique. I, Grundlehren der mathematischen Wissenschaften, vol. 166 (Springer, Berlin, 1971); MR 3075000.Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. I, Publ. Math. Inst. Hautes Études Sci. 20 (1964); MR 173675.CrossRefGoogle Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II, Publ. Math. Inst. Hautes Études Sci. 24 (1965); MR 199181.Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III, Publ. Math. Inst. Hautes Études Sci. 28 (1966); MR 217086.Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV, Publ. Math. Inst. Hautes Études Sci. 32 (1967); MR 238860.Google Scholar
Elkik, R., Singularités rationnelles et déformations, Invent. Math. 47 (1978), 139–147; MR 501926.CrossRefGoogle Scholar
Enescu, F., On the behavior of $F$-rational rings under flat base change, J. Algebra 233 (2000), 543–566; MR 1793916.CrossRefGoogle Scholar
Enescu, F., Local cohomology and $F$-stability, J. Algebra 322 (2009), 3063–3077; MR 2567410.CrossRefGoogle Scholar
Fedder, R., $F$-purity and rational singularity, Trans. Amer. Math. Soc. 278 (1983), 461–480; MR 701505.Google Scholar
Greco, S., A note on universally catenary rings, Nagoya Math. J. 87 (1982), 95–100; MR 676588.CrossRefGoogle Scholar
Greco, S. and Marinari, M. G., Nagata's criterion and openness of loci for Gorenstein and complete intersection, Math. Z. 160 (1978), 207–216; MR 491741.CrossRefGoogle Scholar
Greco, S. and Traverso, C., On seminormal schemes, Compos. Math. 40 (1980), 325–365; MR 571055.Google Scholar
Hall, J. E. and Sharp, R. Y., Dualizing complexes and flat homomorphisms of commutative Noetherian rings, Math. Proc. Cambridge Philos. Soc. 84 (1978), 37–45; MR 480485.CrossRefGoogle Scholar
Hartshorne, R., Residues and duality, Lecture Notes in Mathematics, vol. 20 (Springer, Berlin, 1966), lecture notes of a seminar on the work of A. Grothendieck, given at Harvard 1963/64. With an appendix by P. Deligne; MR 222093.CrossRefGoogle Scholar
Hashimoto, M., Cohen-Macaulay F-injective homomorphisms, in Geometric and combinatorial aspects of commutative algebra (Messina, 1999), Lecture Notes in Pure and Appl. Math., vol. 217 (Dekker, New York, 2001), 231–244; MR 1824233.Google Scholar
Hashimoto, M., F-pure homomorphisms, strong F-regularity, and F-injectivity, Comm. Algebra 38 (2010), 4569–4596; MR 2764840.CrossRefGoogle Scholar
Heitmann, R. C., Lifting seminormality, Michigan Math. J. 57 (2008), 439–445, special volume in honor of Melvin Hochster; MR 2492461.CrossRefGoogle Scholar
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero. I, Ann. of Math. (2) 79 (1964), 109–203; MR 199184.CrossRefGoogle Scholar
Hochster, M. and Huneke, C., $F$-regularity, test elements, and smooth base change, Trans. Amer. Math. Soc. 346 (1994), 1–62; MR 1273534.Google Scholar
Illusie, L., Laszlo, Y. and Orgogozo, F. (eds), Travaux de Gabber sur l'uniformisation locale et la cohomologie étale des schémas quasi-excellents, Séminaire à l’École Polytechnique 2006–2008 Astérisque, vol. 363–364 (Société Mathématique de France, Paris, 2014), with the collaboration of Frédéric Déglise, Alban Moreau, Vincent Pilloni, Michel Raynaud, Joël Riou, Benoît Stroh, Michael Temkin, and Weizhe Zheng; MR 3309086.Google Scholar
Imbesi, M., On a lifting problem in codimension and codepth $k$, Stud. Cerc. Mat. 47 (1995), 51–59; MR 1682595.Google Scholar
Ionescu, C., Sur les anneaux aux fibres formelles géométriquement régulières en codimension $n$, Rev. Roumaine Math. Pures Appl. 31 (1986), 599–603; MR 871813.Google Scholar
Ionescu, C., Cohen Macaulay fibres of a morphism, Atti Accad. Peloritana Pericolanti Cl. Sci. Fis. Mat. Natur. 86 (2008), 1–9.Google Scholar
Ishii, S., Introduction to singularities, second edition (Springer, Tokyo, 2018); MR 3838338.CrossRefGoogle Scholar
Kawamata, Y., Deformations of canonical singularities, J. Amer. Math. Soc. 12 (1999), 85–92; MR 1631527.CrossRefGoogle Scholar
Kawasaki, T., On arithmetic Macaulayfication of Noetherian rings, Trans. Amer. Math. Soc. 354 (2002), 123–149; MR 1859029.CrossRefGoogle Scholar
Kempf, G. R., Knudsen, F. F., Mumford, D. and Saint-Donat, B., Toroidal embeddings. I, Lecture Notes in Mathematics, vol. 339 (Springer, Berlin), 1973; MR 335518.CrossRefGoogle Scholar
Kollár, J., Singularities of the minimal model program, Cambridge Tracts in Mathematics, vol. 200 (Cambridge University Press, Cambridge, 2013), with the collaboration of Sándor Kovács; MR 3057950.CrossRefGoogle Scholar
Kollár, J., Variants of normality for Noetherian schemes, Pure Appl. Math. Q. 12 (2016), 1–31; MR 3613964.CrossRefGoogle Scholar
Kollár, J., Coherence of local and global hulls, Methods Appl. Anal. 24 (2017), 63–70; MR 3694300.CrossRefGoogle Scholar
Kurano, K. and Shimomoto, K., Ideal-adic completion of quasi-excellent rings (after Gabber), Kyoto J. Math. 61 (2021), 707–722; MR 4301055.CrossRefGoogle Scholar
Lipman, J., Desingularization of two-dimensional schemes, Ann. of Math. (2) 107 (1978), 151–207; MR 491722.CrossRefGoogle Scholar
Lipman, J. and Teissier, B., Pseudorational local rings and a theorem of Briançon-Skoda about integral closures of ideals, Michigan Math. J. 28 (1981), 97–116; MR 600418.CrossRefGoogle Scholar
Ma, L. and Schwede, K., Singularities in mixed characteristic via perfectoid big Cohen-Macaulay algebras, Duke Math. J. 170 (2021), 2815–2890; MR 4312190.CrossRefGoogle Scholar
Manaresi, M., Some properties of weakly normal varieties, Nagoya Math. J. 77 (1980), 61–74; MR 556308.CrossRefGoogle Scholar
Marot, J., Sur les anneaux universellement japonais, Bull. Soc. Math. France 103 (1975), 103–111; MR 406995.CrossRefGoogle Scholar
Marot, J., $P$-rings and $P$-homomorphisms, J. Algebra 87 (1984), 136–149; MR 736773.CrossRefGoogle Scholar
Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8, second edition (Cambridge University Press, Cambridge, 1989), translated from the Japanese by Miles Reid; MR 1011461.Google Scholar
Murayama, T., Relative vanishing theorems for Q-schemes, Preprint (2021), arXiv:2101. 10397v2.Google Scholar
Nagata, M., On the closedness of singular loci, Publ. Math. Inst. Hautes Études Sci. 2 (1959), 5–12; MR 106908.CrossRefGoogle Scholar
Nakayama, N., Zariski-decomposition and abundance, MSJ Memoirs, vol. 14. (Mathematical Society of Japan, Tokyo, 2004); MR 2104208.Google ScholarPubMed
Nishimura, J.-i., On ideal-adic completion of Noetherian rings, J. Math. Kyoto Univ. 21 (1981), 153–169; MR 606317.Google Scholar
Nishimura, J.-i. and Nishimura, T., Ideal-adic completion of Noetherian rings. II, Algebraic Geometry and Commutative Algebra, vol. II (Kinokuniya, Tokyo, 1988), 453–467; MR 977773.Google Scholar
Ooishi, A., Openness of loci, $P$-excellent rings and modules, Hiroshima Math. J. 10 (1980), 419–436; MR 577869.CrossRefGoogle Scholar
Patakfalvi, Zs., Schwede, K. and Zhang, W., $F$-singularities in families, Algebr. Geom. 5 (2018), 264–327; MR 3800355.CrossRefGoogle Scholar
Paugam, M., La condition (Gq) de Ischebeck, C. R. Acad. Sci. Paris Sér. A-B 276 (1973), A109–A112, see also [Pau73b]; MR 345955.Google Scholar
Paugam, M., La condition Gq de Ischebeck pour les modules, C. R. Acad. Sci. Paris Sér. A-B 276 (1973), A1031–A1033; MR 345956.Google Scholar
Quillen, D., On the (co-) homology of commutative rings, in Applications of categorical algebra (New York, 1968), Proceedings of Symposia in Pure Mathematics, vol. 17 (American Mathematical Society, Providence, RI, 1970), 65–87; MR 257068.CrossRefGoogle Scholar
Reiten, I. and Fossum, R., Commutative $n$-Gorenstein rings, Math. Scand. 31 (1972), 33–48; MR 376664.CrossRefGoogle Scholar
Rotthaus, C., Komplettierung semilokaler quasiausgezeichneter Ringe, Nagoya Math. J. 76 (1979), 173–180; MR 550860.CrossRefGoogle Scholar
Seydi, H., La théorie des anneaux japonais, Publ. Sém. Math. Univ. Rennes, Exp. no. 12 (1972), 82, Colloque d'Algèbre Commutative (Rennes, 1972); MR 366896.Google Scholar
Shimomoto, K., On the semicontinuity problem of fibers and global $F$-regularity, Comm. Algebra 45 (2017), 1057–1075; MR 3573360.CrossRefGoogle Scholar
Shimomoto, K. and Zhang, W., On the localization theorem for $F$-pure rings, J. Pure Appl. Algebra 213 (2009), 1133–1139, see also [SZ14]; MR 2498803.CrossRefGoogle Scholar
Shimomoto, K. and Zhang, W., Corrigendum to ‘On the localization theorem for $F$-pure rings’, J. Pure Appl. Algebra 218 (2014), 504–505; MR 3124214.CrossRefGoogle Scholar
Smith, K. E., $F$-rational rings have rational singularities, Amer. J. Math. 119 (1997), 159–180; MR 1428062.CrossRefGoogle Scholar
The Stacks project authors, The Stacks project (2020), https://stacks.math.columbia.edu.Google Scholar
Tabaâ, M., Sur les homomorphismes d'intersection complète, C. R. Math. Acad. Sci. Paris Sér. I 298 (1984), 437–439; MR 750740.Google Scholar
Temkin, M., Desingularization of quasi-excellent schemes in characteristic zero, Adv. Math. 219 (2008), 488–522; MR 2435647.CrossRefGoogle Scholar
Valabrega, P., Formal fibers and openness of loci, J. Math. Kyoto Univ. 18 (1978), 199–208; MR 485865.Google Scholar
Vélez, J. D., Openness of the $F$-rational locus and smooth base change, J. Algebra 172 (1995), 425–453; MR 1322412.CrossRefGoogle Scholar
Voevodsky, V., Homology of schemes, Selecta Math. (N.S.) 2 (1996), 111–153; MR 1403354.CrossRefGoogle Scholar