Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T22:35:38.679Z Has data issue: false hasContentIssue false
  • English
  • Français

The two-color Soergel calculus

Part of: Representation theory of groups General commutative ring theory

Published online by Cambridge University Press:  22 September 2015

Ben Elias
Ben Elias*
Affiliation:
Math Department, Fenton Hall, University of Oregon, Eugene, OR 97403, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

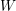We give a diagrammatic presentation for the category of Soergel bimodules for the dihedral group $W$. The (two-colored) Temperley–Lieb category is embedded inside this category as the degree 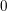$0$ morphisms between color-alternating objects. The indecomposable Soergel bimodules are the images of Jones–Wenzl projectors. When 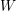$W$ is infinite, the parameter 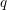$q$ of the Temperley–Lieb algebra may be generic, yielding a quantum version of the geometric Satake equivalence for $\mathfrak{sl}_{2}$. 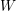When $W$ is finite, 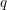$q$ must be specialized to an appropriate root of unity, and the negligible Jones–Wenzl projector yields the Soergel bimodule for the longest element of 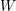$W$.

Keywords

dihedral groupHecke algebraSoergel bimodulesTemperley–Lieb algebraJones–Wenzl projectorgeometric Satakediagrammatics

MSC classification

Primary: 20C08: Hecke algebras and their representations
Secondary: 13A50: Actions of groups on commutative rings; invariant theory
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 2 , February 2016 , pp. 327 - 398
Copyright
© The Author 2015 

References

Bar-Natan, D. and Morrison, S., The Karoubi envelope and Lee’s degeneration of Khovanov homology, Algebr. Geom. Topol. 6 (2006), 1459–1469; MR 2253455 (2008c:57018).CrossRefGoogle Scholar
Barrett, J. W. and Westbury, B. W., Spherical categories, Adv. Math. 143 (1999), 357–375; MR 1686423 (2000c:18007).CrossRefGoogle Scholar
Bigelow, S., Peters, E., Morrison, S. and Snyder, N., Constructing the extended Haagerup planar algebra, Acta Math. 209 (2012), 29–82; MR 2979509.CrossRefGoogle Scholar
Das, P., Ghosh, S. K. and Gupta, V. P., Perturbations of planar algebras, Math. Scand. 114 (2014), 38–85.CrossRefGoogle Scholar
Elias, B., A diagrammatic category for generalized Bott-Samelson bimodules and a diagrammatic categorification of induced trivial modules for Hecke algebras, Preprint (2010), arXiv:1009.2120.Google Scholar
Elias, B., A diagrammatic Temperley-Lieb categorification, Int. J. Math. Math. Sci. (2010), 530808, 47; MR 2726291 (2011j:18015).Google Scholar
Elias, B., Soergel diagrammatics for dihedral groups, PhD thesis, Columbia University (2011).Google Scholar
Elias, B., Quantum Satake in type A: part I, Preprint (2014), arXiv:1403.5570.Google Scholar
Elias, B. and Khovanov, M., Diagrammatics for Soergel categories, Int. J. Math. Math. Sci. (2010), 978635, 58; MR 3095655.CrossRefGoogle Scholar
Elias, B., Snyder, N. and Williamson, G., On cubes of Frobenius extensions, Preprint (2014), arXiv:1308.5994v2.Google Scholar
Elias, B. and Williamson, G., Soergel calculus, Preprint (2013), arXiv:1309.0865.Google Scholar
Elias, B. and Williamson, G., The Hodge theory of Soergel bimodules, Ann. of Math. (2) 180 (2014), 1089–1136; MR 3245013.CrossRefGoogle Scholar
Frenkel, I. B. and Khovanov, M. G., Canonical bases in tensor products and graphical calculus for U q(sl2), Duke Math. J. 87 (1997), 409–480; MR 1446615 (99a:17019).CrossRefGoogle Scholar
Goodman, F. M. and Wenzl, H., Ideals in the Temperley Lieb category, Preprint (2002), arXiv:math/0206301.Google Scholar
Graham, J. J., Modular representations of Hecke algebras and related algebras, PhD thesis, University of Sydney (1996).Google Scholar
Graham, J. J. and Lehrer, G. I., The representation theory of affine Temperley-Lieb algebras, Enseign. Math. (2) 44 (1998), 173–218; MR 1659204 (99i:20019).Google Scholar
Green, R. M., Generalized Temperley-Lieb algebras and decorated tangles, J. Knot Theory Ramifications 7 (1998), 155–171; MR 1618912 (99e:57013).CrossRefGoogle Scholar
Härterich, M., Kazhdan–Lusztig–Basen, unzerlegbare Bimoduln und die Topologie der Fahnenmannigfaltigkeit einer Kac-Moody-Gruppe, PhD thesis, Albert-Ludwigs-Universität Freiburg (1999).Google Scholar
Humphreys, J. E., Reflection groups and Coxeter groups, Cambridge Studies in Advanced Mathematics, vol. 29 (Cambridge University Press, Cambridge, 1990); MR 1066460 (92h:20002).CrossRefGoogle Scholar
Juteau, D., Mautner, C. and Williamson, G., Perverse sheaves and modular representation theory, in Geometric methods in representation theory II, Séminaires et Congrès, vol. 25 (Société Mathématique de France, Paris, 2010), 313–350.Google Scholar
Jones, V. F. R., Index for subfactors, Invent. Math. 72 (1983), 1–25; MR 696688 (84d:46097).CrossRefGoogle Scholar
Jones, V. F. R., Braid groups, Hecke algebras and type II1 factors, in Geometric methods in operator algebras (Kyoto, 1983), Pitman Research Notes in Mathematics Series, vol. 123 (Longman Scientific & Technical, Harlow, 1986), 242–273; MR 866500 (88k:46069).Google Scholar
Jones, V. F. R., The annular structure of subfactors, in Essays on geometry and related topics, Vol. 1, 2, Monogr. Enseign. Math., vol. 38 (Enseignement Math., Geneva, 2001), 401–463; MR 1929335 (2003j:46094).Google Scholar
Kauffman, L. H., State models and the Jones polynomial, Topology 26 (1987), 395–407; MR 899057 (88f:57006).CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras, 53 (1979), 165–184; MR 560412 (81j:20066).CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., Schubert varieties and Poincaré duality, in Geometry of the Laplace operator (Univ. Hawaii, 1979), Proceedings of Symposia in Pure Mathematics, vol. XXXVI (American Mathematical Society, Providence, RI, 1980), 185–203; MR 573434 (84g:14054).CrossRefGoogle Scholar
Khovanov, M., Lauda, A. D., Mackaay, M. and Stošić, M., Extended graphical calculus for categorified quantum sl(2), Mem. Amer. Math. Soc. 219 (2012), MR 2963085.Google Scholar
Lauda, A. D., A categorification of quantum sl(2), Adv. Math. 225 (2010), 3327–3424; MR 2729010 (2012b:17036).CrossRefGoogle Scholar
Libedinsky, N., Sur la catégorie des bimodules de Soergel, J. Algebra 320 (2008), 2675–2694; MR 2441994 (2009h:20008).CrossRefGoogle Scholar
Libedinsky, N., Presentation of right-angled Soergel categories by generators and relations, J. Pure Appl. Algebra 214 (2010), 2265–2278; MR 2660912 (2011k:20078).CrossRefGoogle Scholar
Lusztig, G., Hecke algebras with unequal parameters, CRM Monograph Series, vol. 18 (American Mathematical Society, Providence, RI, 2003); MR 1974442 (2004k:20011).CrossRefGoogle Scholar
Morrison, S., A formula for the Jones-Wenzl projections, Preprint (2015), arXiv:1503.00384.Google Scholar
Soergel, W., Kategorie 𝓞, perverse Garben und Moduln über den Koinvarianten zur Weylgruppe, J. Amer. Math. Soc. 3 (1990), 421–445; MR 1029692 (91e:17007).Google Scholar
Soergel, W., The combinatorics of Harish-Chandra bimodules, J. Reine Angew. Math. 429 (1992), 49–74; MR 1173115 (94b:17011).Google Scholar
Soergel, W., Kazhdan-Lusztig polynomials and a combinatoric[s] for tilting modules, Represent. Theory 1 (1997), 83–114; (electronic). MR 1444322 (98d:17026).CrossRefGoogle Scholar
Soergel, W., On the relation between intersection cohomology and representation theory in positive characteristic, J. Pure Appl. Algebra 152 (2000), 311–335; MR 1784005 (2001k:20098).CrossRefGoogle Scholar
Soergel, W., Kazhdan–Lusztig–Polynome und unzerlegbare Bimoduln über Polynomringen, J. Inst. Math. Jussieu 6 (2007), 501–525; MR 2329762 (2009c:20009).CrossRefGoogle Scholar
Temperley, H. N. V. and Lieb, E. H., Relations between the ‘percolation’ and ‘colouring’ problem and other graph-theoretical problems associated with regular planar lattices: some exact results for the ‘percolation’ problem, Proc. R. Soc. Lond. Ser. A 322 (1971), 251–280; MR 0498284 (58 #16425).Google Scholar
Turaev, V. G., Modular categories and 3-manifold invariants, Internat. J. Modern Phys. B 6 (1992), 1807–1824, MR 1186845 (93k:57040).CrossRefGoogle Scholar
Wenzl, H., On sequences of projections, C. R. Math. Acad. Sci. Soc. R. Can. 9 (1987), 5–9; MR 873400 (88k:46070).Google Scholar
Williamson, G., Singular Soergel bimodules, Int. Math. Res. Not. IMRN 2011 (2011), 4555–4632; MR 2844932.Google Scholar
Williamson, G., Schubert calculus and torsion explosion, Preprint (2013), arXiv:1309.5055.Google Scholar