Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Soldatenkov, Andrey
and
Verbitsky, Misha
2015.
k-symplectic structures and absolutely trianalytic subvarieties in hyperkähler manifolds.
Journal of Geometry and Physics,
Vol. 92,
Issue. ,
p.
147.
Kytmanov, A. A.
Osipov, N. N.
and
Tikhomirov, S. A.
2016.
Finding ein components in the moduli spaces of stable rank 2 bundles on the projective 3-space.
Siberian Mathematical Journal,
Vol. 57,
Issue. 2,
p.
322.
Sanna, Giangiacomo
2016.
Small Charge Instantons and Jumping Lines on the Quintic del Pezzo Threefold.
International Mathematics Research Notices,
p.
rnw198.
Gargate, Michael
and
Jardim, Marcos
2016.
Singular loci of instanton sheaves on projective space.
International Journal of Mathematics,
Vol. 27,
Issue. 07,
p.
1640006.
Lai, Sheng-Hong
2017.
SL(2,C) Instanton Sheaves.
Journal of Physics: Conference Series,
Vol. 804,
Issue. ,
p.
012027.
Jardim, Marcos
Markushevich, Dimitri
and
Tikhomirov, Alexander S.
2017.
Two infinite series of moduli spaces of rank 2 sheaves on
$${\mathbb {P}}^3$$
P
3
.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 196,
Issue. 4,
p.
1573.
Lai, Sheng-Hong
Lee, Jen-Chi
and
Tsai, I-Hsun
2017.
Yang–Mills instanton sheaves.
Annals of Physics,
Vol. 377,
Issue. ,
p.
446.
Jardim, Marcos
Maican, Mario
and
Tikhomirov, Alexander
2017.
Moduli spaces of rank 2 instanton sheaves on the projective space.
Pacific Journal of Mathematics,
Vol. 291,
Issue. 2,
p.
399.
Lai, Sheng-Hong
Lee, Jen-Chi
and
Tsai, I-Hsun
2019.
Yang–Mills instanton sheaves with higher topological charges.
International Journal of Geometric Methods in Modern Physics,
Vol. 16,
Issue. 07,
p.
1950112.
Tikhomirov, A. S.
Tikhomirov, S. A.
and
Vassiliev, D. A.
2019.
Construction of Stable Rank 2 Bundles on ℙ3 Via Symplectic Bundles.
Siberian Mathematical Journal,
Vol. 60,
Issue. 2,
p.
343.
Lai, Sheng-Hong
Lee, Jen-Chi
and
Tsai, I-Hsun
2019.
Sheaf lines of Yang–Mills instanton sheaves.
International Journal of Geometric Methods in Modern Physics,
Vol. 16,
Issue. 03,
p.
1950036.
Kurnosov, Nikon
Soldatenkov, Andrey
and
Verbitsky, Misha
2019.
Kuga-Satake construction and cohomology of hyperkähler manifolds.
Advances in Mathematics,
Vol. 351,
Issue. ,
p.
275.
Tikhomirov, Alexander
and
Vassiliev, Danil
2020.
Construction of symplectic vector bundles on projective space P3.
Journal of Geometry and Physics,
Vol. 158,
Issue. ,
p.
103949.
Antonelli, V.
and
Malaspina, F.
2020.
Instanton bundles on the Segre threefold with Picard number three.
Mathematische Nachrichten,
Vol. 293,
Issue. 6,
p.
1026.
Henni, Abdelmoubine Amar
2020.
On the fixed locus of framed instanton sheaves
on ℙ3.
Pacific Journal of Mathematics,
Vol. 308,
Issue. 1,
p.
41.
Lai, Sheng-Hong
Lee, Jen-Chi
and
Tsai, I-Hsun
2020.
Extended complex Yang–Mills instanton sheaves.
International Journal of Geometric Methods in Modern Physics,
Vol. 17,
Issue. 04,
p.
2050061.
Qin, Xuqiang
2021.
Compactification of the moduli space of minimal instantons on the Fano threefold $$V_4$$.
European Journal of Mathematics,
Vol. 7,
Issue. 4,
p.
1502.
Almeida, C.
Jardim, M.
Tikhomirov, A. S.
and
Tikhomirov, S. A.
2021.
New moduli components of rank 2 bundles on projective space.
Sbornik: Mathematics,
Vol. 212,
Issue. 11,
p.
1503.
Qin, Xuqiang
2021.
Compactification of the moduli space of minimal instantons on the Fano 3-fold V5.
Journal of Pure and Applied Algebra,
Vol. 225,
Issue. 3,
p.
106526.
Almeida, Charles
Jardim, Marcos
Tikhomirov, Alexander Sergeevich
and
Tikhomirov, Sergey Aleksandrovich
2021.
Новые компоненты пространства модулей расслоений ранга 2 на проективном пространстве.
Математический сборник,
Vol. 212,
Issue. 11,
p.
3.
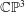 $\mathbb{C}\mathbb{P}^{3}$
$\mathbb{C}\mathbb{P}^{3}$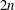 $2n$-manifold is a three-dimensional space
$2n$-manifold is a three-dimensional space 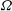 ${\rm\Omega}$ of closed holomorphic forms such that any element of
${\rm\Omega}$ of closed holomorphic forms such that any element of 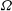 ${\rm\Omega}$ has constant rank
${\rm\Omega}$ has constant rank  $2n$,
$2n$,  $n$ or zero, and degenerate forms in
$n$ or zero, and degenerate forms in 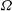 ${\rm\Omega}$ belong to a non-degenerate quadric hypersurface. We show that a trisymplectic manifold is equipped with a holomorphic 3-web and the Chern connection of this 3-web is holomorphic, torsion-free, and preserves the three symplectic forms. We construct a trisymplectic structure on the moduli of regular rational curves in the twistor space of a hyperkähler manifold, and define a trisymplectic reduction of a trisymplectic manifold, which is a complexified form of a hyperkähler reduction. We prove that the trisymplectic reduction in the space of regular rational curves on the twistor space of a hyperkähler manifold
${\rm\Omega}$ belong to a non-degenerate quadric hypersurface. We show that a trisymplectic manifold is equipped with a holomorphic 3-web and the Chern connection of this 3-web is holomorphic, torsion-free, and preserves the three symplectic forms. We construct a trisymplectic structure on the moduli of regular rational curves in the twistor space of a hyperkähler manifold, and define a trisymplectic reduction of a trisymplectic manifold, which is a complexified form of a hyperkähler reduction. We prove that the trisymplectic reduction in the space of regular rational curves on the twistor space of a hyperkähler manifold 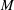 $M$ is compatible with the hyperkähler reduction on
$M$ is compatible with the hyperkähler reduction on 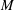 $M$. As an application of these geometric ideas, we consider the ADHM construction of instantons and show that the moduli space of rank
$M$. As an application of these geometric ideas, we consider the ADHM construction of instantons and show that the moduli space of rank  $r$, charge
$r$, charge  $c$ framed instanton bundles on
$c$ framed instanton bundles on 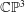 $\mathbb{C}\mathbb{P}^{3}$ is a smooth trisymplectic manifold of complex dimension
$\mathbb{C}\mathbb{P}^{3}$ is a smooth trisymplectic manifold of complex dimension 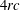 $4rc$. In particular, it follows that the moduli space of rank two, charge
$4rc$. In particular, it follows that the moduli space of rank two, charge  $c$ instanton bundles on
$c$ instanton bundles on 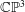 $\mathbb{C}\mathbb{P}^{3}$ is a smooth complex manifold dimension
$\mathbb{C}\mathbb{P}^{3}$ is a smooth complex manifold dimension 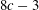 $8c-3$, thus settling part of a 30-year-old conjecture.
$8c-3$, thus settling part of a 30-year-old conjecture.

