Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T04:49:52.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Translates of homogeneous measures associated with observable subgroups on some homogeneous spaces

Part of: Ergodic theory Diophantine equations

Published online by Cambridge University Press:  22 December 2021

Runlin Zhang
Runlin Zhang*
Affiliation:
Beijing International Center for Mathematical Research, Peking University, 1000871Beijing, PR [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present article, we study the following problem. Let 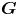$\boldsymbol {G}$ be a linear algebraic group over 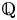$\mathbb {Q}$, let 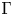$\Gamma$ be an arithmetic lattice, and let 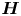$\boldsymbol {H}$ be an observable 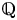$\mathbb {Q}$-subgroup. There is a 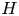$H$-invariant measure 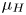$\mu _H$ supported on the closed submanifold 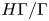$H\Gamma /\Gamma$. Given a sequence 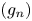$(g_n)$ in 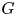$G$, we study the limiting behavior of 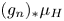$(g_n)_*\mu _H$ under the weak-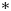$*$ topology. In the non-divergent case, we give a rather complete classification. We further supplement this by giving a criterion of non-divergence and prove non-divergence for arbitrary sequence 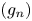$(g_n)$ for certain large 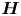$\boldsymbol {H}$. We also discuss some examples and applications of our result. This work can be viewed as a natural extension of the work of Eskin–Mozes–Shah and Shapira–Zheng.

Keywords

homogeneous dynamicsintegral pointsequidistribution

MSC classification

Primary: 37A17: Homogeneous flows
Secondary: 11D45: Counting solutions of Diophantine equations
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 12 , December 2021 , pp. 2657 - 2698
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bialynicki-Birula, A., Hochschild, G. and Mostow, G. D., Extensions of representations of algebraic linear groups, Amer. J. Math. 85 (1963), 131–144; MR155938.CrossRefGoogle Scholar
Borel, A. and De Siebenthal, J., Les sous-groupes fermés de rang maximum des groupes de Lie clos, Comment. Math. Helv. 23 (1949), 200–221; MR0032659.CrossRefGoogle Scholar
Borel, A. and Harish-Chandra, Arithmetic subgroups of algebraic groups, Ann. of Math. (2) 75 (1962), 485–535; MR0147566.CrossRefGoogle Scholar
Benoist, Y. and Oh, H., Effective equidistribution of $S$-integral points on symmetric varieties, Ann. Inst. Fourier (Grenoble) 62 (2012), 1889–1942; MR3025156.CrossRefGoogle Scholar
Borel, A., Introduction to arithmetic groups, University Lecture Series, vol. 73 (American Mathematical Society, Providence, RI, 2019). Translated from the 1969 French original [MR0244260] by Lam Laurent Pham, edited and with a preface by Dave Witte Morris; MR3970984.CrossRefGoogle Scholar
Benedetti, R. and Petronio, C., Lectures on hyperbolic geometry, Universitext (Springer, Berlin, 1992); MR1219310.CrossRefGoogle Scholar
Benoist, Y. and Quint, J.-F., Random walks on finite volume homogeneous spaces, Invent. Math. 187 (2012), 37–59; MR2874934.CrossRefGoogle Scholar
Borel, A. and Serre, J.-P., Corners and arithmetic groups, Comment. Math. Helv. 48 (1973), 436–491. Avec un appendice: Arrondissement des variétés à coins, par A. Douady et L. Hérault; MR0387495.CrossRefGoogle Scholar
Dani, S. G. and Margulis, G. A., Limit distributions of orbits of unipotent flows and values of quadratic forms, I.M. Gel´fand Seminar (Advances in Soviet Mathematics), vol. 16 (American Mathematical Society, Providence, RI, 1993), 91–137; MR1237827.Google Scholar
Duke, W., Rudnick, Z. and Sarnak, P., Density of integer points on affine homogeneous varieties, Duke Math. J. 71 (1993), 143–179; MR1230289.CrossRefGoogle Scholar
David, O. and Shapira, U., Equidistribution of divergent orbits and continued fraction expansion of rationals, J. Lond. Math. Soc. (2) 98 (2018), 149–176; MR3847236.CrossRefGoogle Scholar
David, O. and Shapira, U., Equidistribution of divergent orbits of the diagonal group in the space of lattices, Ergodic Theory Dynam. Systems 40 (2020), 1217–1237; MR4082261.CrossRefGoogle Scholar
Eskin, A. and McMullen, C., Mixing, counting, and equidistribution in Lie groups, Duke Math. J. 71 (1993), 181–209; MR1230290.CrossRefGoogle Scholar
Einsiedler, M., Margulis, G., Mohammadi, A. and Venkatesh, A., Effective equidistribution and property $(\tau )$, J. Amer. Math. Soc. 33 (2020), 223–289; MR4066475.CrossRefGoogle Scholar
Eskin, A., Mozes, S. and Shah, N., Unipotent flows and counting lattice points on homogeneous varieties, Ann. of Math. (2) 143 (1996), 253–299; MR1381987.CrossRefGoogle Scholar
Eskin, A., Mozes, S. and Shah, N., Non-divergence of translates of certain algebraic measures, Geom. Funct. Anal. 7 (1997), 48–80; MR1437473.CrossRefGoogle Scholar
Eskin, A., Mozes, S. and Shah, N., Correction to ‘Unipotent flows and counting lattice points on homogeneous spaces’ (1998), https://people.math.osu.edu/shah.595/correctionfinal.pdf.Google Scholar
Gille, P., The Borel-De Siebenthal's theorem, Preprint (2010), http://math.univ-lyon1.fr/homes-www/gille/prenotes/bds.pdf.Google Scholar
Gorodnik, A., Maucourant, F. and Oh, H., Manin's and Peyre's conjectures on rational points and adelic mixing, Ann. Sci. Éc. Norm. Supér. (4) 41 (2008), 383–435; MR2482443.Google Scholar
Gorodnik, A. and Oh, H., Rational points on homogeneous varieties and equidistribution of adelic periods, Geom. Funct. Anal. 21 (2011), 319–392, with an appendix by Mikhail Borovoi; MR2795511.CrossRefGoogle Scholar
Grosshans, F. D., Algebraic homogeneous spaces and invariant theory, Lecture Notes in Mathematics, vol. 1673 (Springer, Berlin, 1997); MR1489234.CrossRefGoogle Scholar
Kempf, G. R., Instability in invariant theory, Ann. of Math. (2) 108 (1978), 299–316; MR506989.CrossRefGoogle Scholar
Kelmer, D. and Kontorovich, A., Effective equidistribution of shears and applications, Math. Ann. 370 (2018), 381–421; MR3747491.CrossRefGoogle Scholar
Kelmer, D. and Kontorovich, A., Exponents for the equidistribution of shears and applications, Preprint (2018), arXiv:1802.09452.Google Scholar
Kleinbock, D. Y. and Margulis, G. A., Flows on homogeneous spaces and Diophantine approximation on manifolds, Ann. of Math. (2) 148 (1998), 339–360; MR1652916.CrossRefGoogle Scholar
Mozes, S. and Shah, N., On the space of ergodic invariant measures of unipotent flows, Ergodic Theory Dynam. Systems 15 (1995), 149–159; MR1314973.CrossRefGoogle Scholar
Oh, H. and Shah, N. A., Limits of translates of divergent geodesics and integral points on one-sheeted hyperboloids, Israel J. Math. 199 (2014), 915–931; MR3219562.CrossRefGoogle Scholar
Raghunathan, M. S., Discrete subgroups of Lie groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 68 (Springer, New York–Heidelberg, 1972); MR0507234.CrossRefGoogle Scholar
Ratner, M., On Raghunathan's measure conjecture, Ann. of Math. (2) 134 (1991), 545–607; MR1135878.CrossRefGoogle Scholar
Richard, R. and Shah, N. A., Geometric results on linear actions of reductive Lie groups for applications to homogeneous dynamics, Ergodic Theory Dynam. Systems 38 (2018), 2780–2800; MR3846726.CrossRefGoogle Scholar
Richard, R. and Zamojski, T., Limit distribution of Translated pieces of possibly irrational leaves in S-arithmetic homogeneous spaces, Preprint (2016), arXiv:1604.08494.Google Scholar
Siegel, C. L., Symplectic geometry, Amer. J. Math. 65 (1943), 1–86; MR8094.CrossRefGoogle Scholar
Springer, T. A., Linear algebraic groups, second edition, Progress in Mathematics, vol. 9 (Birkhäuser, Boston, MA, 1998); MR1642713.CrossRefGoogle Scholar
Shapira, U. and Zheng, C., Limiting distributions of translates of divergent diagonal orbits, Compos. Math. 155 (2019), 1747–1793.CrossRefGoogle Scholar
Vinberg, É. B. and Popov, V. L., Invariant theory, in Algebraic geometry, 4 (Russian), Itogi Nauki i Tekhniki (Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1989), 137–314, 315; MR1100485.Google Scholar
Weiss, B., Finite-dimensional representations and subgroup actions on homogeneous spaces, Israel J. Math. 106 (1998), 189–207; MR1656889.CrossRefGoogle Scholar
Zamojski, T., Counting rational matrices of a fixed irreducible characteristic polynomial, PhD thesis, The University of Chicago (ProQuest LLC, 2010); MR2941378.Google Scholar
Zhang, R., Limiting distribution of translates of the orbit of a maximal $\mathbb {Q}$-torus from identity on $\text {SL}_n(\mathbb {R})/\text {SL}_n(\mathbb {Z})$, Math. Ann. 375 (2019), 1231–1281.CrossRefGoogle Scholar