Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-13T12:23:20.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Trace and Künneth formulas for singularity categories and applications

Part of: Algebraic number theory: local and $p$-adic fields Topological $K$-theory

Published online by Cambridge University Press:  03 June 2022

Bertrand Toën  and
Gabriele Vezzosi
Bertrand Toën
Affiliation:
IMT, CNRS, Université de Toulouse, 118, route de Narbonne, 31062 Toulouse Cedex 9, France [email protected]
Gabriele Vezzosi
Affiliation:
DIMAI, Università di Firenze, Viale Morgagni, 67/a, 50134 Firenze, Italy [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an 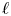$\ell$-adic trace formula for saturated and admissible dg-categories over a base monoidal differential graded (dg)-category. Moreover, we prove Künneth formulas for dg-category of singularities and for inertia-invariant vanishing cycles. As an application, we prove a categorical version of Bloch's conductor conjecture (originally stated by Spencer Bloch in 1985), under the additional hypothesis that the monodromy action of the inertia group is unipotent.

Keywords

trace formulasnon-commutative geometryvanishing cyclesBloch's conductor conjecture

MSC classification

Secondary: 19L10: Riemann-Roch theorems, Chern characters 11S15: Ramification and extension theory
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 3 , March 2022 , pp. 483 - 528
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

BT is partially supported by ERC-2016-ADG-741501 and ANR-11-LABX-0040-CIMI within the program ANR-11-IDEX-0002-02.

References

Beilinson, A. A. and Bernstein, J., A proof of Jantzen conjectures, in I. M. Gel'fand seminar, Advances in Soviet Mathematics, vol. 16, eds Gel'fand, S., Gindikin, S. (American Mathematical Society, Providence, RI, 1993), 1–50.Google Scholar
Blanc, A., Topological K-theory of complex noncommutative spaces, Compos. Math. 152 (2016), 489–555.10.1112/S0010437X15007617CrossRefGoogle Scholar
Blanc, A., Robalo, M., Toën, B. and Vezzosi, G., Motivic realizations of singularity categories and vanishing cycles, J. Éc. Polytech. 5 (2018), 651–747.CrossRefGoogle Scholar
Bloch, S., Cycles on arithmetic schemes and Euler characteristics of curves, in Algebraic geometry-Bowdoin 1985, Part 2, Proceedings of Symposia in Pure Mathematics, vol. 46 (American Mathematical Society, Providence, RI, 1987), 421–450.CrossRefGoogle Scholar
Gaitsgory, D. and Lurie, J., Weil's conjecture over function fields, Preprint, http://www.math.harvard.edu/~lurie/papers/tamagawa.pdf.Google Scholar
Haugseng, R., The higher Morita category of $E_n$-algebras, Geom. Topol. 21 (2017), 1631–1730.CrossRefGoogle Scholar
Hovey, M., Model categories, Mathematical Surveys and Monographs, vol. 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Illusie, L., Autour du théorème de monodromie locale, in Périodes p-adiques, Séminaire de Bures, 1988, Astérisque, vol. 223 (Société Mathématique de France, 1994), 9–57.Google Scholar
Illusie, L., Around the Thom-Sebastiani theorem, with an appendix by Weizhe Zheng, Manuscripta Math. 152 (2017), 61–125.CrossRefGoogle Scholar
Illusie, L., Laszlo, Y. and Orgogozo, F., Travaux de Gabber sur l'uniformisation locale et la cohomologie et́ale des schémas quasi-excellents, Astérisque, vol. 363–364 (Société Mathématique de France, 2014).Google Scholar
Kapranov, M., On DG-modules over the de Rham complex and the vanishing cycles functor, in Algebraic geometry (Chicago, IL, 1989), Lecture Notes in Mathematics, vol. 1479 (Springer, Berlin, 1991), 57–86.CrossRefGoogle Scholar
Kato, K. and Saito, T., On the conductor formula of Bloch, Publ. Math. Inst. Hautes Études Sci. 100 (2005), 5–151.CrossRefGoogle Scholar
Lurie, J., Higher Algebra, Preprint (2016), http://www.math.harvard.edu/~lurie/papers/HA.pdf.Google Scholar
Lurie, J., On the classification of topological field theories, Current Developments in Mathematics, vol. 2008 (International Press, Somerville, MA, 2009), 129–280; MR2555928 (2010k:57064).Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, 2009).10.1515/9781400830558CrossRefGoogle Scholar
Neukirch, J., Algebraic number theory, Grundlehren der Mathematischen Wissenschaften, vol. 322 (Springer, Berlin, 1999).CrossRefGoogle Scholar
Orgogozo, F., Conjecture de Bloch et nombres de Milnor, Ann. Inst. Fourier (Grenoble) 53 (2003), 1739–1754.CrossRefGoogle Scholar
Preygel, A., Thom-Sebastiani & duality for matrix factorizations, Thesis, Preprint (2011), arXiv:1101.5834.Google Scholar
Robalo, M., K-theory and the bridge from motives to non-commutative motives, Adv. Math. 269 (2015), 399–550.CrossRefGoogle Scholar
Saito, T., Characteristic cycles and the conductor of direct image, Preprint (2017), arXiv:1704.04832.Google Scholar
Serre, J.-P., Linear representations of finite groups, Graduate Texts in Mathematics, vol. 42 (Springer, Berlin, 1977).CrossRefGoogle Scholar
Artin, M., Grothendieck, A. and Verdier, J.-L. (eds), Séminaire de Géométrie Algébrique du Bois Marie – 1963–64 – Théorie des topos et cohomologie étale des schémas – (SGA 4) – vol. 3, Lecture Notes in Mathematics, vol. 305 (Springer, Berlin, New York, 1972).Google Scholar
Grothendieck, A., Séminaire de Géométrie Algébrique du Bois Marie – 1967–69 – Groupes de monodromie en géométrie algébrique – (SGA 7) – vol. 1, Lecture Notes in Mathematics, vol. 288 (Springer, Berlin, New York, 1972).Google Scholar
Deligne, P. and Katz, N. (eds), Séminaire de Géométrie Algébrique du Bois Marie – 1967–69 – Groupes de monodromie en géométrie algébrique – (SGA 7) – vol. 2, Lecture Notes in Mathematics, vol. 340 (Springer, Berlin, New York, 1973).Google Scholar
Toën, B., DG-categories and derived Morita theory, Invent. Math. 167 (2007), 615–667.CrossRefGoogle Scholar
Toën, B., Lectures on dg-categories, in Topics in algebraic and topological K-theory, Lecture Notes in Mathematics, vol. 2008 (Springer, Berlin, 2011), 243–302.Google Scholar
Toën, B., Derived Azumaya algebras and generators for twisted derived categories, Invent. Math. 189 (2012), 581–652.CrossRefGoogle Scholar
Toën, B. and Vaquié, M., Moduli of objects in dg-categories, Ann. Sci. Éc. Norm. Supér. (4) 40 (2007), 387–444.CrossRefGoogle Scholar
Toën, B. and Vezzosi, G., Caractères de Chern, traces équivariantes et géométrie algébrique dérivée, Selecta Math. (N.S.) 21 (2015), 449–554.10.1007/s00029-014-0158-6CrossRefGoogle Scholar
Toën, B. and Vezzosi, G., Géométrie non-commutative, formule des traces et conducteur de Bloch, in Actes du 1er congrès national de la SMF, Séminaires et Congrès, vol. 31, ed. Lecouvrey, C. (Société Mathématique de France, 2018), 77–107.Google Scholar
Voevodsky, V., $\mathbb {A}^{1}$-homotopy theory, in Proceedings of the International Congress of Mathematicians, Documenta Mathematica, Extra Volume ICM 1998, vol. I (Deutsche Mathematiker-Vereinigung, Berlin, 1998), 579–604.Google Scholar