Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-09T01:33:42.915Z Has data issue: false hasContentIssue false
  • English
  • Français

Thin monodromy in Sp(4)

Part of: Families, fibrations

Published online by Cambridge University Press:  10 March 2014

Christopher Brav  and
Hugh Thomas
Christopher Brav
Affiliation:
Mathematical Institute, University of Oxford, 24–29 St Giles’, Oxford OX1 3LB, UK email [email protected]
Hugh Thomas
Affiliation:
Department of Mathematics and Statistics, University of New Brunswick, Fredericton, New Brunswick, Canada E3B 5A3 email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

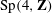We show that some hypergeometric monodromy groups in ${\rm Sp}(4,\mathbf{Z})$ split as free or amalgamated products and hence by cohomological considerations give examples of Zariski dense, non-arithmetic monodromy groups of real rank 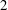$2$. In particular, we show that the monodromy group of the natural quotient of the Dwork family of quintic threefolds in 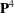$\mathbf{P}^{4}$ splits as 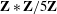$\mathbf{Z}\ast \mathbf{Z}/5\mathbf{Z}$. As a consequence, for a smooth quintic threefold 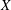$X$ we show that the group of autoequivalences 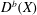$D^{b}(X)$ generated by the spherical twist along 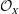${\mathcal{O}}_{X}$ and by tensoring with ${\mathcal{O}}_{X}(1)$ is an Artin group of dihedral type.

Keywords

Dwork familymonodromythin groupsping-pong lemma

MSC classification

Secondary: 14D05: Structure of families (Picard-Lefschetz, monodromy, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 3 , March 2014 , pp. 333 - 343
Copyright
© The Author(s) 2014 

References

Beukers, F. and Heckman, G., Monodromy for the hypergeometric function nF n−1, Invent. Math. 95 (1989), 325–354; MR 974906 (90f:11034).Google Scholar
Canonaco, A. and Karp, R. L., Derived autoequivalences and a weighted Beilinson resolution, J. Geom. Phys. 58 (2008), 743–760.Google Scholar
Chen, Y.-H., Yang, Y. and Yui, N., Monodromy of Picard–Fuchs differential equations for Calabi–Yau threefolds, J. Reine Angew. Math. 616 (2008), 167–203; with an appendix by Cord Erdenberger; MR 2369490 (2009m:32046).Google Scholar
Deligne, P. and Mostow, G. D., Monodromy of hypergeometric functions and nonlattice integral monodromy, Publ. Math. Inst. Hautes Études Sci. 63 (1986), 5–89; MR 849651 (88a:22023a).Google Scholar
Doran, C. F. and Morgan, J. W., Mirror symmetry and integral variations of Hodge structure underlying one-parameter families of Calabi–Yau threefolds, in Mirror symmetry. V, AMS/IP Studies in Advanced Mathematics, vol. 38 (American Mathematical Society, Providence, RI, 2006), 517–537; MR 2282973 (2008e:14010).Google Scholar
van Enckevort, C. and van Straten, D., Monodromy calculations of fourth order equations of Calabi–Yau type, in Mirror symmetry. V, AMS/IP Studies in Advanced Mathematics, vol. 38 (American Mathematical Society, Providence, RI, 2006), 539–559; MR 2282974 (2007m:14057).Google Scholar
Fuchs, E., Meiri, C. and Sarnak, P., Hyperbolic monodromy groups for the hypergeometric equation and Cartan involutions, Preprint (2013), arXiv:1305.0729.Google Scholar
Griffiths, P. and Schmid, W., Recent developments in Hodge theory: a discussion of techniques and results, in Discrete subgroups of Lie groups and applications to moduli (Internat. Colloq., Bombay, 1973) (Oxford University Press, Bombay, 1975), 31–127; MR 0419850 (54 #7868).Google Scholar
Kuznetsov, A. G., Derived category of a cubic threefold and the variety $V_{14}$, Tr. Mat. Inst. Steklova 246 (2004), no. Algebr. Geom. Metody, Svyazi i Prilozh., 183–207;MR 2101293 (2005i:14049).Google Scholar
Lee, R. and Weintraub, S. H., Cohomology of Sp4(Z)and related groups and spaces, Topology 24 (1985), 391–410; MR 816521 (87b:11044).Google Scholar
Lyndon, R. C. and Schupp, P. E.,Combinatorial group theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 89 (Springer, Berlin, 1977); MR 0577064 (58 #28182).Google Scholar
Nori, M. V., A nonarithmetic monodromy group, C. R. Acad. Sci. Paris Sér. I Math. 302 (1986), 71–72; MR 832040 (87g:14008).Google Scholar
Sarnak, P., Notes on thin matrix groups, Preprint (2012), arXiv:1212.3525.Google Scholar
Singh, S. and Venkataramana, T. N., Arithmeticity of certain symplectic hypergeometric groups, Preprint (2012), arXiv:1208.6460.Google Scholar
Stein, W. A. et al. , Sage mathematics software (Version 5.3), The Sage Development Team, 2012, http://www.sagemath.org.Google Scholar
Swan, R. G., Groups of cohomological dimension one, J. Algebra 12 (1969), 585–610; MR 0240177 (39 #1531).Google Scholar