Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T19:08:51.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity

Part of: Discontinuous groups and automorphic forms Lie groups

Published online by Cambridge University Press:  15 December 2020

Yueke Hu  and
Abhishek Saha
Yueke Hu
Affiliation:
Yau Mathematical Sciences Center, Tsinghua University, Beijing100084, [email protected]
Abhishek Saha
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, LondonE1 4NS, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We improve upon the local bound in the depth aspect for sup-norms of newforms on 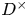$D^\times$, where 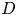$D$ is an indefinite quaternion division algebra over 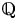${\mathbb {Q}}$. Our sup-norm bound implies a depth-aspect subconvexity bound for 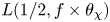$L(1/2, f \times \theta _\chi )$, where 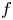$f$ is a (varying) newform on 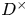$D^\times$ of level 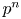$p^n$, and 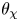$\theta _\chi$ is an (essentially fixed) automorphic form on 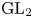$\textrm {GL}_2$ obtained as the theta lift of a Hecke character 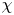$\chi$ on a quadratic field. For the proof, we augment the amplification method with a novel filtration argument and a recent counting result proved by the second-named author to reduce to showing strong quantitative decay of matrix coefficients of local newvectors along compact subsets, which we establish via 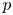$p$-adic stationary phase analysis. Furthermore, we prove a general upper bound in the level aspect for sup-norms of automorphic forms belonging to any family whose associated matrix coefficients have such a decay property.

Keywords

automorphic formnewformMaass formsubconvexitysup-normamplificationL-functionlevel aspectdepth aspectmatrix coefficientquaternion algebra

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Secondary: 11F12: Automorphic forms, one variable 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols 11F72: Spectral theory; Selberg trace formula 11F85: $p$-adic theory, local fields 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 11 , November 2020 , pp. 2368 - 2398
Check for updates
Copyright
© The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assing, E., On the size of $p$-adic Whittaker functions, Trans. Amer. Math. Soc. 372 (2019), 5287–5340.CrossRefGoogle Scholar
Blomer, V., Epstein zeta-functions, subconvexity, and the purity conjecture, J. Inst. Math. Jussieu 19 (2018), 1–16.Google Scholar
Blomer, V., Harcos, G., Maga, P. and Milićević, D., The sup-norm problem for $\textrm {GL}(2)$ over number fields, J. Eur. Math. Soc. (JEMS) 22 (2020), 1–53.CrossRefGoogle Scholar
Blomer, V. and Holowinsky, R., Bounding sup-norms of cusp forms of large level, Invent. Math. 179 (2010), 645–681.CrossRefGoogle Scholar
Bushnell, C. J. and Henniart, G., The local Langlands conjecture for GL(2) (Springer, Berlin, 2006).CrossRefGoogle Scholar
Corbett, A. and Saha, A., On the order of vanishing of newforms at cusps, Math. Res. Lett. 25 (2018), 1771–1804.CrossRefGoogle Scholar
File, D., Martin, K. and Pitale, A., Test vectors and central $L$-values for $\textrm {GL}(2)$, Algebra Number Theory 11 (2017), 253–318.CrossRefGoogle Scholar
Gelbart, S., Automorphic forms on adèle groups, Annals of Mathematics Studies, vol. 83 (Princeton University Press–University of Tokyo Press, Princeton, NJ–Tokyo, 1975).CrossRefGoogle Scholar
Gross, B. H., Local orders, root numbers, and modular curves, Amer. J. Math. 110 (1988), 1153–1182.CrossRefGoogle Scholar
Harcos, G. and Michel, P., The subconvexity problem for Rankin–Selberg $L$-functions and equidistribution of Heegner points. II, Invent. Math. 163 (2006), 581–655.CrossRefGoogle Scholar
Harcos, G. and Templier, N., On the sup-norm of Maass cusp forms of large level. II, Int. Math. Res. Not. IMRN 2012 (2012), 4764–4774.CrossRefGoogle Scholar
Harcos, G. and Templier, N., On the sup-norm of Maass cusp forms of large level. III, Math. Ann. 356 (2013), 209–216.CrossRefGoogle Scholar
Harris, M. and Kudla, S. S., The central critical value of a triple product $L$-function, Ann. of Math. (2) 133 (1991), 605–672.CrossRefGoogle Scholar
Hu, Y., Triple product formula and the subconvexity bound of triple product $L$-function in level aspect, Amer. J. Math. 139 (2017), 215–259.CrossRefGoogle Scholar
Hu, Y., Triple product formula and mass equidistribution on modular curves of level $N$, Int. Math. Res. Not. IMRN 2018 (2018), 2899–2943.Google Scholar
Hu, Y. and Nelson, P. D., New test vector for Waldspurger's period integral, Preprint (2018), arXiv:1810.11564v1.Google Scholar
Hu, Y., Nelson, P. D. and Saha, A., Some analytic aspects of automorphic forms on $\textrm {GL}(2)$ of minimal type, Comment. Math. Helv. 94 (2019), 767–801.CrossRefGoogle Scholar
Humphries, P. and Khan, R., On the random wave conjecture for dihedral Maaß forms, Geom. Funct. Anal. 30 (2020), 34–125.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, American Mathematical Society Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Iwaniec, H. and Sarnak, P., $L^{\infty }$ norms of eigenfunctions of arithmetic surfaces, Ann. of Math. (2) 141 (1995), 301–320.CrossRefGoogle Scholar
Kowalski, E., Michel, P. and VanderKam, J., Rankin–Selberg $L$-functions in the level aspect, Duke Math. J. 114 (2002), 123–191.CrossRefGoogle Scholar
Marshall, S., Local bounds for $L^p$ norms of Maass forms in the level aspect, Algebra Number Theory 10 (2016), 803–812.CrossRefGoogle Scholar
Michel, P. and Venkatesh, A., The subconvexity problem for $\textrm {GL}_2$, Publ. Math. Inst. Hautes Études Sci. 111 (2010), 171–271.CrossRefGoogle Scholar
Nordentoft, A., Hybrid subconvexity for class group L-functions and uniform sup norm bounds of Eisenstein series, Forum Math. (2020), https://doi.org/10.1515/forum-2019-0173.CrossRefGoogle Scholar
Oh, H., Uniform pointwise bounds for matrix coefficients of unitary representations and applications to Kazhdan constants, Duke Math. J. 113 (2002), 133–192.CrossRefGoogle Scholar
Rohrlich, D., Elliptic curves and the Weil–Deligne group, in Elliptic curves and related topics, CRM Proceedings and Lecture Notes, vol. 4 (American Mathematical Society, Providence, RI, 1994), 125–157.CrossRefGoogle Scholar
Saha, A., Large values of newforms on $\textrm {GL}(2)$ with highly ramified central character, Int. Math. Res. Not. IMRN 2016 (2016), 4103–4131.CrossRefGoogle Scholar
Saha, A., Hybrid sup-norm bounds for Maass newforms of powerful level, Algebra Number Theory 11 (2017), 1009–1045.CrossRefGoogle Scholar
Saha, A., Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, Math. Ann. 376 (2020), 609–644.CrossRefGoogle Scholar
Sarnak, P., Arithmetic quantum chaos, Blyth Lectures, Toronto (1993). Available at http://publications.ias.edu/sites/default/files/Arithmetic%20Quantum%20Chaos.pdf.Google Scholar
Sawin, W., A geometric approach to the sup-norm problem for automorphic forms: the case of newforms on $GL_2(\mathbb {F}_q(T))$ with squarefree level, Preprint (2019), arXiv:1907.08098.Google Scholar
Shalika, J. A. and Tanaka, S., On an explicit construction of a certain class of automorphic forms, Amer. J. Math. 91 (1969), 1049–1076.CrossRefGoogle Scholar
Templier, N., On the sup-norm of Maass cusp forms of large level, Selecta Math. (N.S.) 16 (2010), 501–531.CrossRefGoogle Scholar
Tunnell, J. B., On the local Langlands conjecture for $\textrm {GL}(2)$, Invent. Math. 46 (1978), 179–200.CrossRefGoogle Scholar
Waldspurger, J.-L., Sur les valeurs de certaines fonctions $L$ automorphes en leur centre de symétrie, Compos. Math. 54 (1985), 173–242.Google Scholar
Wu, H. and Andersen, N., Explicit subconvexity for GL2 and some applications, Preprint (2018), arXiv:1812.04391.Google Scholar
Young, M. P., A note on the sup norm of Eisenstein series, Q. J. Math. 69 (2018), 1151–1161.Google Scholar