Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T15:35:02.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Supernatural analogues of Beilinson monads

Part of: Commutative algebra: Homological methods (Co)homology theory

Published online by Cambridge University Press:  14 November 2016

Daniel Erman  and
Steven V Sam
Daniel Erman
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, WI 53706-1325, USA email [email protected]
Steven V Sam
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840, USA Current address: Department of Mathematics, University of Wisconsin, Madison, WI 53706-1325, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We use supernatural bundles to build 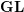$\mathbf{GL}$ -equivariant resolutions supported on the diagonal of 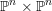$\mathbb{P}^{n}\times \mathbb{P}^{n}$ , in a way that extends Beilinson’s resolution of the diagonal. We thus obtain results about supernatural bundles that largely parallel known results about exceptional collections. We apply this construction to Boij–Söderberg decompositions of cohomology tables of vector bundles, yielding a proof of concept for the idea that those positive rational decompositions should admit meaningful categorifications.

Keywords

Sheaf cohomologymonadsBoij–Söderberg theory

MSC classification

Primary: 14F05: Sheaves, derived categories of sheaves and related constructions 13D02: Syzygies, resolutions, complexes
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 12 , December 2016 , pp. 2545 - 2562
Copyright
© The Authors 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ancona, V. and Ottaviani, G., An introduction to derived categories and a theorem of Beilinson , Atti Accad. Peloritana Pericolanti Cl. Sci. Fis. Mat. Natur. 67 (1989), 99–110.Google Scholar
Beĭlinson, A. A., Coherent sheaves on P n and problems in linear algebra , Funktsional. Anal. i Prilozhen. 12 (1978), 68–69.Google Scholar
Berkesch, C., Erman, D., Kummini, M. and Sam, S. V, Poset structures in Boij–Söderberg theory , Int. Math. Res. Not. IMRN 22 (2012), 5132–5160.Google Scholar
Berkesch Zamaere, C., Erman, D., Kummini, M. and Sam, S. V, Tensor complexes: multilinear free resolutions constructed from higher tensors , J. Eur. Math. Soc. (JEMS) 15 (2013), 2257–2295.Google Scholar
Bernstein, I. N., Gelfand, I. M. and Gelfand, S. I., Algebraic vector bundles on P n and problems of linear algebra , Funktsional. Anal. i Prilozhen. 12 (1978), 66–67.Google Scholar
Boij, M. and Söderberg, J., Graded Betti numbers of Cohen–Macaulay modules and the multiplicity conjecture , J. Lond. Math. Soc. (2) 78 (2008), 85–106.Google Scholar
Boij, M. and Söderberg, J., Betti numbers of graded modules and the multiplicity conjecture in the non-Cohen–Macaulay case , Algebra Number Theory 6 (2012), 437–454.Google Scholar
Canonaco, A., Exceptional sequences and derived autoequivalences, Preprint (2008),arXiv:0801.0173v1.Google Scholar
Eisenbud, D., Commutative algebra with a view toward algebraic geometry, Graduate Texts in Mathematics, vol. 150 (Springer, New York, 1995).Google Scholar
Eisenbud, D. and Erman, D., Categorified duality in Boij–Söderberg theory and invariants of free complexes, J. Eur. Math. Soc. (JEMS), to appear. Preprint (2012), arXiv:1205.0449v2.Google Scholar
Eisenbud, D., Erman, D. and Schreyer, F.-O., Filtering free resolutions , Compositio Math. 149 (2013), 754–772; corrigendum: Compositio Math. 150 (2014), 1482–1484.Google Scholar
Eisenbud, D., Fløystad, G. and Schreyer, F.-O., Sheaf cohomology and free resolutions over exterior algebras , Trans. Amer. Math. Soc. 355 (2003), 4397–4426.Google Scholar
Eisenbud, D., Fløystad, G. and Weyman, J., The existence of equivariant pure free resolutions , Ann. Inst. Fourier (Grenoble) 61 (2011), 905–926.Google Scholar
Eisenbud, D. and Schreyer, F.-O., Betti numbers of graded modules and cohomology of vector bundles , J. Amer. Math. Soc. 22 (2009), 859–888.Google Scholar
Eisenbud, D. and Schreyer, F.-O., Cohomology of coherent sheaves and series of supernatural bundles , J. Eur. Math. Soc. (JEMS) 12 (2010), 703–722.Google Scholar
Eisenbud, D. and Schreyer, F.-O., Betti numbers of syzygies and cohomology of coherent sheaves, Proceedings of the International Congress of Mathematicians, vol. II (Hindustan Book Agency, New Delhi, 2010), 586–602.Google Scholar
Eisenbud, D. and Schreyer, F.-O., The banks of the cohomology river , Kyoto J. Math. 53 (2013), 131–144.Google Scholar
Fløystad, G., Boij–Sderberg theory: introduction and survey, Progress in Commutative Algebra, vol. 1 (de Gruyter, Berlin, 2012), 1–54.Google Scholar
Fulton, W. and Harris, J., Representation theory. A first course, Graduate Texts in Mathematics, vol. 129 (Springer, New York, 1991).Google Scholar
Gorodentsev, A. L. and Rudakov, A. N., Exceptional vector bundles on projective spaces , Duke Math. J. 54 (1987), 115–130.CrossRefGoogle Scholar
Hartshorne, R. and Hirschowitz, A., Cohomology of a general instanton bundle , Ann. Sci. Éc. Norm. Supér. (4) 15 (1982), 365–390.Google Scholar
Huybrechts, D., Fourier–Mukai transforms in algebraic geometry, Oxford Mathematical Monographs (Clarendon Press, Oxford, 2006).Google Scholar
Kummini, M. and Sam, S. V, The cone of Betti tables over a rational normal curve , in Commutative algebra and noncommutative algebraic geometry, Mathematical Sciences Research Institute Publications, vol. 68 (Cambridge University Press, Cambridge, 2015), 251–264.Google Scholar
Lazarsfeld, R., Positivity in algebraic geometry. I. Classical setting: line bundles and linear series, A Series of Modern Surveys in Mathematics, vol. 48 (Springer, Berlin, 2004).Google Scholar
Sam, S. V and Snowden, A., GL-equivariant modules over polynomial rings in infinitely many variables , Transactions of the American Mathematical Society 368 (2016), 1097–1158.Google Scholar
Sam, S. V and Weyman, J., Pieri resolutions for classical groups , J. Algebra 329 (2011), 222–259; special issue celebrating the 60th birthday of Corrado De Concini.Google Scholar
Weyman, J., Cohomology of vector bundles and syzygies, Cambridge Tracts in Mathematics, vol. 149 (Cambridge University Press, Cambridge, 2003).Google Scholar