Article contents
The strong Suslin reciprocity law
Published online by Cambridge University Press: 01 April 2021
Abstract
We prove the strong Suslin reciprocity law conjectured by A. Goncharov. The Suslin reciprocity law is a generalization of the Weil reciprocity law to higher Milnor 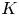 $K$-theory. The Milnor
$K$-theory. The Milnor 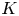 $K$-groups can be identified with the top cohomology groups of the polylogarithmic motivic complexes; Goncharov's conjecture predicts the existence of a contracting homotopy underlying Suslin reciprocity. The main ingredient of the proof is a homotopy invariance theorem for the cohomology of the polylogarithmic motivic complexes in the ‘next to Milnor’ degree. We apply these results to the theory of scissors congruences of hyperbolic polytopes. For every triple of rational functions on a compact projective curve over
$K$-groups can be identified with the top cohomology groups of the polylogarithmic motivic complexes; Goncharov's conjecture predicts the existence of a contracting homotopy underlying Suslin reciprocity. The main ingredient of the proof is a homotopy invariance theorem for the cohomology of the polylogarithmic motivic complexes in the ‘next to Milnor’ degree. We apply these results to the theory of scissors congruences of hyperbolic polytopes. For every triple of rational functions on a compact projective curve over 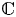 $\mathbb {C}$ we construct a hyperbolic polytope (defined up to scissors congruence). The hyperbolic volume and the Dehn invariant of this polytope can be computed directly from the triple of rational functions on the curve.
$\mathbb {C}$ we construct a hyperbolic polytope (defined up to scissors congruence). The hyperbolic volume and the Dehn invariant of this polytope can be computed directly from the triple of rational functions on the curve.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2021
References
- 4
- Cited by



