Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T01:18:07.592Z Has data issue: false hasContentIssue false
  • English
  • Français

Simultaneous deformations and Poisson geometry

Part of: Lie algebras and Lie superalgebras General theory of differentiable manifolds Pseudogroups, differentiable groupoids and general structures on manifolds Symplectic geometry, contact geometry

Published online by Cambridge University Press:  04 May 2015

Yaël Frégier  and
Marco Zambon
Yaël Frégier
Affiliation:
UArtois, LML, F-62 300, Lens, France MIT, 77 Massachusetts Avenue, Cambridge, MA 02139, USA Universität Zürich, Winterthurerstr. 190, CH-8057 Zürich, Switzerland email [email protected]
Marco Zambon
Affiliation:
Universidad Autónoma de Madrid, Spain email [email protected], [email protected] ICMAT (CSIC-UAM-UC3M-UCM), Campus de Cantoblanco, 28049 Madrid, Spain Current address: KU Leuven, Department of Mathematics, Celestijnenlaan 200B box 2400, BE-3001 Leuven, Belgium. email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

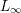We consider the problem of deforming simultaneously a pair of given structures. We show that such deformations are governed by an $L_{\infty }$-algebra, which we construct explicitly. Our machinery is based on Voronov’s derived bracket construction. In this paper we consider only geometric applications, including deformations of coisotropic submanifolds in Poisson manifolds, of twisted Poisson structures, and of complex structures within generalized complex geometry. These applications cannot be, to our knowledge, obtained by other methods such as operad theory.

Keywords

L∞ -algebradeformationMaurer–Cartan equationPoisson manifoldDirac manifoldgeneralized complex manifold

MSC classification

Primary: 17B70: Graded Lie (super)algebras 53D17: Poisson manifolds; Poisson groupoids and algebroids 58H15: Deformations of structures
Secondary: 53D18: Generalized geometries (à la Hitchin) 58A50: Supermanifolds and graded manifolds
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 9 , September 2015 , pp. 1763 - 1790
Copyright
© The Authors 2015 

References

Barnich, G., Fulp, R., Lada, T. and Stasheff, J., The SH Lie structure of Poisson brackets in field theory, Comm. Math. Phys. 191 (1998), 585–601.CrossRefGoogle Scholar
Bayen, F., Flato, M., Fronsdal, C., Lichnerowicz, A. and Sternheimer, D., Quantum mechanics as a deformation of classical mechanics, Lett. Math. Phys. 1 (1977), 521–530.CrossRefGoogle Scholar
Bursztyn, H., Crainic, M. and Ševera, P., Quasi-Poisson structures as Dirac structures, in Travaux mathématiques, Fasc. XVI (University of Luxembourg, Luxembourg, 2005), 41–52.Google Scholar
Cannas da Silva, A. and Weinstein, A., Geometric models for noncommutative algebras, Berkeley Mathematics Lecture Notes, vol. 10 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Cattaneo, A. S. and Felder, G., Relative formality theorem and quantisation of coisotropic submanifolds, Adv. Math. 208 (2007), 521–548.CrossRefGoogle Scholar
Cattaneo, A. S. and Schätz, F., Introduction to supergeometry, Rev. Math. Phys. 23 (2011), 669–690.CrossRefGoogle Scholar
Courant, T., Dirac manifolds, Trans. Amer. Math. Soc. 319 (1990), 631–661.CrossRefGoogle Scholar
Fiorenza, D. and Manetti, M., L ∞ structures on mapping cones, Algebra Number Theory 1 (2007), 301–330.CrossRefGoogle Scholar
Frégier, Y., Markl, M. and Yau, D., The L ∞ -deformation complex of diagrams of algebras, New York J. Math. 15 (2009), 353–392.Google Scholar
Frégier, Y. and Zambon, M., Simultaneous deformations of algebras and morphisms via derived brackets, J. Pure Appl. Algebra, accepted, arXiv:1301.4864.Google Scholar
Fukaya, K., Deformation theory, homological algebra and mirror symmetry, in Geometry and physics of branes (Como, 2001), Series in High Energy Physics, Cosmology and Gravitation (IOP, Bristol, 2003), 121–209; http://www.mat.uniroma1.it/people/manetti/GeoSup0708/fukaya.pdf.Google Scholar
Gerstenhaber, M., On the deformation of rings and algebras, Ann. of Math. (2) 79 (1964), 55–70.CrossRefGoogle Scholar
Getzler, E., Lie theory for nilpotent L ∞ -algebras, Ann. of Math. (2) 170 (2009), 271–301.CrossRefGoogle Scholar
Getzler, E., Homotopy theory for $L_{\infty }$-algebras. Course given at the workshop Higher structure in topology and geometry IV, Göttingen, 2–4 June (2010). Partial notes available athttp://nlab.mathforge.org/nlab/show/descent+for+L-infinity+algebras.Google Scholar
Getzler, E., The automorphism 3-group of the 2-groupoid of Poisson brackets on a manifold, Talk at the conference Poisson 2010, Rio de Janeiro, August (2010).Google Scholar
Gualtieri, M., Generalized complex geometry, Ann. of Math. (2) 174 (2011), 75–123.CrossRefGoogle Scholar
Hitchin, N., Generalized Calabi–Yau manifolds, Q. J. Math. 54 (2003), 281–308.CrossRefGoogle Scholar
Ji, X., Simultaneous deformation of Lie algebroids and Lie subalgebroids, J. Geom. Phys. 84 (2014), 8–29.CrossRefGoogle Scholar
Kodaira, K. and Spencer, D., On deformations of complex-analytic structures I, Ann. of Math. (2) 67 (1958), 328–401.CrossRefGoogle Scholar
Kodaira, K. and Spencer, D., On deformations of complex-analytic structures II, Ann. of Math. (2) 67 (1958), 403–466.CrossRefGoogle Scholar
Kodaira, K. and Spencer, D., On deformations of complex-analytic structures III, Ann. of Math. (2) 71 (1960), 43–76.CrossRefGoogle Scholar
Kontsevich, M., Deformation quantization of Poisson manifolds, Lett. Math. Phys. 66 (2003), 157–216.CrossRefGoogle Scholar
Kontsevich, M. and Soibelman, Y., Deformation theory. I. Draft.http://www.math.ksu.edu/∼soibel/Book-vol1.ps.Google Scholar
Kosmann-Schwarzbach, Y., Derived brackets, Lett. Math. Phys. 69 (2004), 61–87.CrossRefGoogle Scholar
Kosmann-Schwarzbach, Y., Quasi, twisted, and all that … in Poisson geometry and Lie algebroid theory, in The breadth of symplectic and Poisson geometry, Progress in Mathematics, vol. 232 (Birkhäuser, Boston, MA, 2005), 363–389.Google Scholar
Kuranishi, M., New proof for the existence of locally complete families of complex structures, in Proc. conf. complex analysis (Minneapolis, 1964) (Springer, 1965).Google Scholar
Lada, T. and Markl, M., Strongly homotopy Lie algebras, Comm. Algebra 23 (1995), 2147–2161.CrossRefGoogle Scholar
Lada, T. and Stasheff, J., Introduction to SH Lie algebras for physicists, Internat. J. Theoret. Phys. 7 (1993), 1087–1103.CrossRefGoogle Scholar
Liu, Z.-J., Weinstein, A. and Xu, P., Manin triples for Lie bialgebroids, J. Differential Geom. 45 (1997), 547–574.CrossRefGoogle Scholar
Loday, J. L. and Vallette, B., Algebraic operads, Grundlehren der Mathematischen Wissenschaften, vol. 346 (Springer, Heidelberg, 2012).CrossRefGoogle Scholar
Merkulov, S. A., An L ∞ -algebra of an unobstructed deformation functor, Int. Math. Res. Not. IMRN 2000 (2000), 147–164.CrossRefGoogle Scholar
Merkulov, S. and Vallette, B., Deformation theory of representation of prop(erad)s II, J. reine angew. Math. 636 (2009), 125–174.Google Scholar
Nijenhuis, A. and Richardson, R. W. Jr., Cohomology and deformations in graded Lie algebras, Bull. Amer. Math. Soc. (N.S.) 72 (1966), 1–29.CrossRefGoogle Scholar
Nijenhuis, A. and Richardson, R. W. Jr., Deformations of homomorphisms of Lie groups and Lie algebras, Bull. Amer. Math. Soc. (N.S.) 73 (1967), 175–179.CrossRefGoogle Scholar
Oh, Y.-G. and Park, J.-S., Deformations of coisotropic submanifolds and strong homotopy Lie algebroids, Invent. Math. 161 (2005), 287–360.CrossRefGoogle Scholar
Park, J.-S., Topological open p-branes, in Symplectic geometry and mirror symmetry (Seoul, 2000) (World Scientific, River Edge, NJ, 2001), 311–384.CrossRefGoogle Scholar
Roytenberg, D., Courant algebroids, derived brackets and even symplectic supermanifolds, PhD thesis, University of California, Berkeley (1999), arXiv:math/9910078.Google Scholar
Roytenberg, D., On the structure of graded symplectic supermanifolds and Courant algebroids, in Quantization, Poisson brackets and beyond (Manchester, 2001), Contemporary Mathematics, vol. 315 (American Mathematical Society, Providence, RI, 2002), 169–185.CrossRefGoogle Scholar
Roytenberg, D., Quasi-Lie bialgebroids and twisted Poisson manifolds, Lett. Math. Phys. 61 (2002), 123–137.CrossRefGoogle Scholar
Schätz, F., Coisotropic submanifolds and the BFV-complex, PhD thesis, University of Zürich (2009), http://home.imf.au.dk/fschaetz/writings.html.Google Scholar
Schätz, F. and Zambon, M., Deformations of coisotropic submanifolds for fibrewise entire Poisson structures, Lett. Math. Phys. 103 (2013), 777–791.CrossRefGoogle Scholar
Ševera, P. and Weinstein, A., Poisson geometry with a 3-form background, Progr. Theoret. Phys. Suppl. 144 (2001), 145–154 (Noncommutative geometry and string theory, Proceedings of International Workshop, Yokohama, 2001).CrossRefGoogle Scholar
Voronov, T., Higher derived brackets and homotopy algebras, J. Pure Appl. Algebra 202 (2005), 133–153.CrossRefGoogle Scholar
Voronov, T., Higher derived brackets for arbitrary derivations, in Travaux mathématiques, Fasc. XVI (University of Luxembourg, Luxembourg, 2005), 163–186.Google Scholar
Zambon, M., L ∞ -algebras and higher analogues of Dirac structures and Courant algebroids, J. Symplectic Geom. 10 (2012), 563–599.CrossRefGoogle Scholar