Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T04:44:53.139Z Has data issue: false hasContentIssue false
  • English
  • Français

Robinson’s conjecture on heights of characters

Part of: Representation theory of groups

Published online by Cambridge University Press:  20 May 2019

Zhicheng Feng ,
Conghui Li ,
Yanjun Liu ,
Gunter Malle  and
Jiping Zhang
Zhicheng Feng
Affiliation:
School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China email [email protected]
Conghui Li
Affiliation:
Department of Mathematics, Southwest Jiaotong University, Chengdu 611756, China email [email protected]
Yanjun Liu
Affiliation:
College of Mathematics and Information Science, Jiangxi Normal University, Nanchang, China email [email protected]
Gunter Malle
Affiliation:
FB Mathematik, TU Kaiserslautern, Postfach 3049, 67653 Kaiserslautern, Germany email [email protected]
Jiping Zhang
Affiliation:
School of Mathematical Sciences, Peking University, Beijing 100871, China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Geoffrey Robinson conjectured in 1996 that the 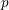$p$-part of character degrees in a 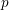$p$-block of a finite group can be bounded in terms of the center of a defect group of the block. We prove this conjecture for all primes 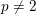$p\neq 2$ for all finite groups. Our argument relies on a reduction by Murai to the case of quasi-simple groups which are then studied using deep results on blocks of finite reductive groups.

Keywords

Robinson’s conjectureheights of charactersdefects of characters

MSC classification

Primary: 20C15: Ordinary representations and characters 20C33: Representations of finite groups of Lie type
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 6 , June 2019 , pp. 1098 - 1117
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first and fourth authors gratefully acknowledge financial support by SFB TRR 195, and the others by NSFC (No. 11631001). In addition, the third author gratefully acknowledges financial support by NSFC (No. 11661042) and the Key Laboratory of Mathematics and Its Applications of Peking University.

References

Bessenrodt, C. and Olsson, J. B., Heights of spin characters in characteristic 2 , in Finite reductive groups, related structures and representations (Birkhäuser, Boston, 1997), 51–71.Google Scholar
Bonnafé, C., Dat, J.-F. and Rouquier, R., Derived categories and Deligne–Lusztig varieties II , Ann. of Math. (2) 185 (2017), 609–670.Google Scholar
Brauer, R., Investigations on group characters , Ann. of Math. (2) 42 (1941), 936–958.Google Scholar
Brauer, R., On blocks and sections in finite groups. II , Amer. J. Math. 90 (1968), 895–925.Google Scholar
Broué, M., Malle, G. and Michel, J., Generic blocks of finite reductive groups , Astérisque 212 (1993), 7–92.Google Scholar
Cabanes, M. and Enguehard, M., On unipotent blocks and their ordinary characters , Invent. Math. 117 (1994), 149–164.Google Scholar
Cabanes, M. and Enguehard, M., Representation theory of finite reductive groups (Cambridge University Press, Cambridge, 2004).Google Scholar
Carter, R., Finite groups of Lie type: conjugacy classes and complex characters (Wiley, Chichester, 1985).Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of finite groups (Clarendon Press, Oxford, 1984).Google Scholar
Eaton, C. W., The equivalence of some conjectures of Dade and Robinson , J. Algebra 271 (2004), 638–651.Google Scholar
Enguehard, M., Sur les l-blocs unipotents des groupes réductifs finis quand l est mauvais , J. Algebra 230 (2000), 334–377.Google Scholar
Enguehard, M., Towards a Jordan decomposition of blocks of finite reductive groups, Preprint (2013), arXiv:1312.0106.Google Scholar
Fong, P., On the characters of p-solvable groups , Trans. Amer. Math. Soc. 98 (1961), 263–284.Google Scholar
GAP Group, GAP – groups, algorithms, and programming, Version 4.8.10 (2018),http://www.gap-system.org.Google Scholar
Geck, M., On the p-defects of character degrees of finite groups of Lie type , Carpathian J. Math. 19 (2003), 97–100.Google Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The classification of the finite simple groups, Mathematical Surveys and Monographs, vol. 40.3 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Kessar, R. and Malle, G., Quasi-isolated blocks and Brauer’s height zero conjecture , Ann. of Math. (2) 178 (2013), 321–384.Google Scholar
Landrock, P., The non-principal 2-blocks of sporadic simple groups , Comm. Algebra 6 (1978), 1865–1891.Google Scholar
Lusztig, G., Characters of reductive groups over a finite field, Annals of Mathematics Studies, vol. 107 (Princeton University Press, Princeton, NJ, 1984).Google Scholar
Malle, G., Die unipotenten Charaktere von 2 F 4(q 2) , Comm. Algebra 18 (1990), 2361–2381.Google Scholar
Malle, G., The maximal subgroups of  2 F 4(q 2) , J. Algebra 139 (1991), 52–69.Google Scholar
Malle, G., Height 0 characters of finite groups of Lie type , Represent. Theory 11 (2007), 192–220.Google Scholar
Malle, G. and Testerman, D., Linear algebraic groups and finite groups of Lie type, Cambridge Studies in Advanced Mathematics, vol. 133 (Cambridge University Press, Cambridge, 2011).Google Scholar
Murai, M., Blocks of factor groups and heights of characters , Osaka J. Math. 35 (1998), 835–854.Google Scholar
Navarro, G., Characters and blocks of finite groups, London Mathematical Society Lecture Note Series, vol. 250 (Cambridge University Press, Cambridge, 1998).Google Scholar
Olsson, J. B., Combinatorics and representations of finite groups (Universität Essen, Fachbereich Mathematik, Essen, 1993).Google Scholar
Ree, R., A family of simple groups associated with the simple Lie algebra of type (F 4) , Amer. J. Math. 83 (1961), 401–420.Google Scholar
Ree, R., A family of simple groups associated with the simple Lie algebra of type (G 2) , Amer. J. Math. 83 (1961), 432–462.Google Scholar
Robinson, G., Local structure, vertices and Alperin’s conjecture , Proc. Lond. Math. Soc. (3) 72 (1996), 312–330.Google Scholar
Sambale, B., Blocks of finite groups and their invariants, Lecture Notes in Mathematics, vol. 2127 (Springer, Cham, 2014).Google Scholar
Syskin, S. A., Abstract properties of the simple sporadic groups , Uspekhi Mat. Nauk 35 (1980), 181–212.Google Scholar
Wagner, A., An observation on the degrees of projective representations of the symmetric and alternating group over an arbitrary field , Arch. Math. 29 (1977), 583–589.Google Scholar
Watanabe, A., On Fong’s reductions , Kumamoto J. Sci. (Math.) 13 (1978/79), 48–54.Google Scholar
Wilson, R. A., The finite simple groups, Graduate Texts in Mathematics, vol. 251 (Springer, London, 2009).Google Scholar