Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T15:36:08.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Right-angled Artin groups as normal subgroups of mapping class groups

Part of: Low-dimensional topology Special aspects of infinite or finite groups

Published online by Cambridge University Press:  27 July 2021

Matt Clay ,
Johanna Mangahas  and
Dan Margalit
Matt Clay
Affiliation:
Department of Mathematical Sciences, University of Arkansas, 309 SCEN, Fayetteville, AR72701, [email protected]
Johanna Mangahas
Affiliation:
Department of Mathematics, University at Buffalo, 244 Mathematics Building, Buffalo, NY14260, [email protected]
Dan Margalit
Affiliation:
School of Mathematics, Georgia Institute of Technology, 686 Cherry Street, Atlanta, GA30332, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct the first examples of normal subgroups of mapping class groups that are isomorphic to non-free right-angled Artin groups. Our construction also gives normal, non-free right-angled Artin subgroups of other groups, such as braid groups and pure braid groups, as well as many subgroups of the mapping class group, such as the Torelli subgroup. Our work recovers and generalizes the seminal result of Dahmani–Guirardel–Osin, which gives free, purely pseudo-Anosov normal subgroups of mapping class groups. We give two applications of our methods: (1) we produce an explicit proper normal subgroup of the mapping class group that is not contained in any level 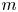$m$ congruence subgroup and (2) we produce an explicit example of a pseudo-Anosov mapping class with the property that all of its even powers have free normal closure and its odd powers normally generate the entire mapping class group. The technical theorem at the heart of our work is a new version of the windmill apparatus of Dahmani–Guirardel–Osin, which is tailored to the setting of group actions on the projection complexes of Bestvina–Bromberg–Fujiwara.

Keywords

mapping class groupright-angled Artin group

MSC classification

Secondary: 57M07: Topological methods in group theory 20F65: Geometric group theory
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 8 , August 2021 , pp. 1807 - 1852
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Behrstock, J. A., Asymptotic geometry of the mapping class group and Teichmüller space, Geom. Topol. 10 (2006), 1523–1578; MR 2255505.10.2140/gt.2006.10.1523CrossRefGoogle Scholar
Bestvina, M., Personal communication, May 2018.Google Scholar
Bestvina, M., Bromberg, K. and Fujiwara, K., Bounded cohomology via quasi-trees, Preprint, (2013), arXiv:1306.1542v1.Google Scholar
Bestvina, M., Bromberg, K. and Fujiwara, K., Constructing group actions on quasi-trees and applications to mapping class groups, Publ. Math. Inst. Hautes Études Sci. 122 (2015), 1–64; MR 3415065.CrossRefGoogle Scholar
Bestvina, M., Bromberg, K., Fujiwara, K. and Sisto, A., Acylindrical actions on projection complexes, Enseign. Math. 65 (2019), 1–32; MR 4057354.CrossRefGoogle Scholar
Bestvina, M., Dickmann, R., Domat, G., Kwak, S., Patel, P. and Stark, E., Free products from spinning and rotating families, Preprint (2020), arXiv:2010.10735.Google Scholar
Bestvina, M. and Feighn, M., Hyperbolicity of the complex of free factors, Adv. Math. 256 (2014), 104–155; MR 3177291.CrossRefGoogle Scholar
Bestvina, M. and Fujiwara, K., Bounded cohomology of subgroups of mapping class groups, Geom. Topol. 6 (2002), 69–89; MR 1914565 (2003f:57003).CrossRefGoogle Scholar
Birman, J. S., Lubotzky, A. and McCarthy, J., Abelian and solvable subgroups of the mapping class groups, Duke Math. J. 50 (1983), 1107–1120; MR 726319.CrossRefGoogle Scholar
Bowditch, B., Tight geodesics in the curve complex, Invent. Math. 171 (2008), 218–300; MR 2367021.CrossRefGoogle Scholar
Brendle, T. and Margalit, D., Normal subgroups of mapping class groups and the metaconjecture of Ivanov, J. Amer. Math. Soc. 32 (2019), 1009–1070; MR 4013739.CrossRefGoogle Scholar
Clay, M. T., Leininger, C. J. and Mangahas, J., The geometry of right-angled Artin subgroups of mapping class groups, Groups Geom. Dyn. 6 (2012), 249–278; MR 2914860.CrossRefGoogle Scholar
Clay, M., Leininger, C. J. and Margalit, D., Abstract commensurators of right-angled Artin groups and mapping class groups, Math. Res. Lett. 21 (2014), 461–467; MR 3272023.10.4310/MRL.2014.v21.n3.a4CrossRefGoogle Scholar
Clay, M. and Mangahas, J., Hyperbolic quotients of projection complexes, Groups Geom. Dyn., to appear.Google Scholar
Crisp, J. and Farb, B., The prevalence of surface subgroups in mapping class groups, Preprint.Google Scholar
Crisp, J. and Paris, L., The solution to a conjecture of Tits on the subgroup generated by the squares of the generators of an Artin group, Invent. Math. 145 (2001), 19–36; MR 1839284.CrossRefGoogle Scholar
Crisp, J. and Wiest, B., Quasi-isometrically embedded subgroups of braid and diffeomorphism groups, Trans. Amer. Math. Soc. 359 (2007), 5485–5503; MR 2327038.CrossRefGoogle Scholar
Dahmani, F., The normal closure of big Dehn twists and plate spinning with rotating families, Geom. Topol. 22 (2018), 4113–4144; MR 3890772.10.2140/gt.2018.22.4113CrossRefGoogle Scholar
Dahmani, F., Guirardel, V. and Osin, D., Hyperbolically embedded subgroups and rotating families in groups acting on hyperbolic spaces, Mem. Amer. Math. Soc. 245 (2017); MR 3589159.Google Scholar
Dahmani, F., Hagen, M. and Sisto, A., Dehn filling Dehn twists, Proc. Roy. Soc. Edinburgh Sect. A 151 (2021), 28–51; MR 4202630.CrossRefGoogle Scholar
Farb, B., Some problems on mapping class groups and moduli space, in Problems on mapping class groups and related topics, Proceedings of Symposia in Pure Mathematics, vol. 74 (American Mathematical Society, Providence, RI, 2006), 11–55; MR 2264130.Google Scholar
Farb, B. and Margalit, D., A primer on mapping class groups, Princeton Mathematical Series, vol. 49 (Princeton University Press, Princeton, NJ, 2012); MR 2850125.Google Scholar
Fathi, A., Laudenbach, F. and Poenaru, V., Travaux de Thurston sur les surfaces (Séminaire Orsay) (Société Mathématique de France, Paris, 1991). Reprint of Travaux de Thurston sur les surfaces, Astérisque No. 66-67 (Société Mathématique de France, Paris, 1979) [MR 0568308 (82m:57003)]; MR 1134426.Google Scholar
Fujiwara, K., Subgroups generated by two pseudo-Anosov elements in a mapping class group. II. Uniform bound on exponents, Trans. Amer. Math. Soc. 367 (2015), 4377–4405; MR 3324932.CrossRefGoogle Scholar
Gromov, M., ${\rm CAT}(\kappa )$-spaces: construction and concentration, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 280 (2001), no. Geom. i Topol. 7, 100–140, 299–300; MR 1879258.Google Scholar
Hamidi-Tehrani, H., Groups generated by positive multi-twists and the fake lantern problem, Algebr. Geom. Topol. 2 (2002), 1155–1178; MR 1943336.CrossRefGoogle Scholar
Hensel, S., Przytycki, P. and Webb, R. C. H., 1-slim triangles and uniform hyperbolicity for arc graphs and curve graphs, J. Eur. Math. Soc. (JEMS) 17 (2015), 755–762; MR 3336835.CrossRefGoogle Scholar
Hull, M., Small cancellation in acylindrically hyperbolic groups, Groups Geom. Dyn. 10 (2016), 1077–1119; MR 3605028CrossRefGoogle Scholar
Ishida, A., The structure of subgroup of mapping class groups generated by two Dehn twists, Proc. Japan Acad. Ser. A Math. Sci. 72 (1996), 240–241; MR 1435728CrossRefGoogle Scholar
Ivanov, N. V., Subgroups of Teichmüller modular groups, Translations of Mathematical Monographs, vol. 115 (American Mathematical Society, Providence, RI, 1992). Translated from the Russian by E. J. F. Primrose and revised by the author. MR 1195787.Google Scholar
Ivanov, N. V., Fifteen problems about the mapping class groups, in Problems on mapping class groups and related topics, Proceedings of Symposia in Pure Mathematics, vol. 74 (American Mathematical Society, Providence, RI, 2006), 71–80; MR 2264532.Google Scholar
Koberda, T., Right-angled Artin groups and a generalized isomorphism problem for finitely generated subgroups of mapping class groups, Geom. Funct. Anal. 22 (2012), 1541–1590; MR 3000498.CrossRefGoogle Scholar
Lanier, J. and Margalit, D., Normal generators for mapping class groups are abundant (first version), Preprint (2018), arXiv:1805.03666v1.Google Scholar
Lanier, J. and Margalit, D., Normal generators for mapping class groups are abundant, Preprint (2020), arXiv:1805.03666.Google Scholar
Leininger, C., Personal communication, January 2019.Google Scholar
Lönne, M., Presentations of subgroups of the braid group generated by powers of band generators, Topology Appl. 157 (2010), 1127–1135; MR 2607077.CrossRefGoogle Scholar
Loving, M., Personal communication, January 2019.Google Scholar
Mangahas, J., Uniform uniform exponential growth of subgroups of the mapping class group, Geom. Funct. Anal. 19 (2010), 1468–1480; MR 2585580 (2011d:57002).10.1007/s00039-009-0038-yCrossRefGoogle Scholar
Mangahas, J., A recipe for short-word pseudo-Anosovs, Amer. J. Math. 135 (2013), 1087–1116; MR 3086070.CrossRefGoogle Scholar
Mann, K. and Rafi, K., Large scale geometry of big mapping class groups, Preprint (2020), arXiv:1912.10914.Google Scholar
Masur, H. A. and Minsky, Y. N., Geometry of the complex of curves. I. Hyperbolicity, Invent. Math. 138 (1999), 103–149; MR 1714338 (2000i:57027).CrossRefGoogle Scholar
Masur, H. A. and Minsky, Y. N., Geometry of the complex of curves. II. Hierarchical structure, Geom. Funct. Anal. 10 (2000), 902–974; MR 1791145 (2001k:57020).CrossRefGoogle Scholar
McCarthy, J., A “Tits-alternative” for subgroups of surface mapping class groups, Trans. Amer. Math. Soc. 291 (1985), 583–612; MR 800253.Google Scholar
Minasyan, A., Personal communication, June 2019.Google Scholar
Runnels, I., Effective generation of right-angled Artin groups in mapping class groups, Preprint (2020), arXiv:2004.13585.Google Scholar
Seo, D., Powers of Dehn twists generating right-angled Artin groups, Preprint (2019), arXiv:1909.03394.Google Scholar
Serre, J.-P., Trees, Springer Monographs in Mathematics (Springer, Berlin, 2003), translated from the French original by John Stillwell, corrected 2nd printing of the 1980 English translation; MR 1954121 (2003m:20032).Google Scholar
Thurston, W. P., On the geometry and dynamics of diffeomorphisms of surfaces, Bull. Amer. Math. Soc. (N.S.) 19 (1988), 417–431; MR 956596.CrossRefGoogle Scholar
Whittlesey, K., Normal all pseudo-Anosov subgroups of mapping class groups, Geom. Topol. 4 (2000), 293–307; MR 1786168.CrossRefGoogle Scholar