Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T22:49:22.597Z Has data issue: false hasContentIssue false
  • English
  • Français

Représentations banales de 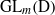${\rm GL}_{m}({\rm D})$

Part of: Lie groups

Published online by Cambridge University Press:  02 January 2013

Alberto Mínguez  and
Vincent Sécherre
Alberto Mínguez
Affiliation:
Institut de Mathématiques de Jussieu, Université Pierre et Marie Curie, 4, place Jussieu, 75005 Paris, France (email: [email protected])
Vincent Sécherre
Affiliation:
Université de Versailles Saint-Quentin-en-Yvelines, Laboratoire de Mathématiques de Versailles, 45 avenue des Etats-Unis, 78035 Versailles cedex, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 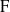${\rm F}$ be a non-Archimedean locally compact field of residue characteristic 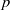$p$, let 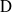${\rm D}$ be a finite-dimensional central division 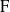${\rm F}$-algebra and let 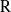${\rm R}$ be an algebraically closed field of characteristic different from 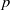$p$. We define banal irreducible 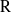${\rm R}$-representations of the group 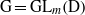${\rm G}={\rm GL}_{m}({\rm D})$. This notion involves a condition on the cuspidal support of the representation depending on the characteristic of 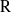${\rm R}$. When this characteristic is banal with respect to 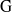${\rm G}$, in particular when 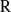${\rm R}$ is the field of complex numbers, any irreducible 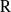${\rm R}$-representation of 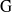${\rm G}$ is banal. In this article, we give a classification of all banal irreducible 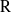${\rm R}$-representations of 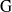${\rm G}$ in terms of certain multisegments, called banal. When 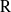${\rm R}$ is the field of complex numbers, our method provides a new proof, entirely local, of Tadić’s classification of irreducible complex smooth representations of 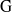${\rm G}$.

Keywords

representations of $p$-adic groupsmodular representationmultisegmentbanal representation

MSC classification

Secondary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 4 , April 2013 , pp. 679 - 704
Copyright
Copyright © 2013 The Author(s)

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[Ari02]Ariki, S., Representations of quantum algebras and combinatorics of Young tableaux, University Lecture Series, vol. 26 (American Mathematical Society, Providence, RI, 2002).CrossRefGoogle Scholar
[Aub95]Aubert, A.-M., Dualité dans le groupe de Grothendieck de la catégorie des représentations lisses de longueur finie d’un groupe réductif $p$-adique, Trans. Amer. Math. Soc. 347 (1995), 2179–2189.Google Scholar
[Aub96]Aubert, A.-M., Erratum à Dualité dans le groupe de Grothendieck de la catégorie des représentations lisses de longueur finie d’un groupe réductif $p$-adique, Trans. Amer. Math. Soc. 348 (1996), 4687–4690.CrossRefGoogle Scholar
[Aue04]Auel, A. N., Une démonstration d’un théorème de Bernstein sur les représentations de quasi carré intégrable de ${{\rm {G}{L}}}_{n}({F})$où ${F}$est un corps local non archimédien, Mémoire de DEA, Université Paris Sud (2004).Google Scholar
[Bad04]Badulescu, A. I., Un résultat d’irréductibilité en caractéristique non nulle, Tohoku Math. J. (2) 56 (2004), 583–592.Google Scholar
[BHLS10]Badulescu, A. I., Henniart, G., Lemaire, B. and Sécherre, V., Sur le dual unitaire de ${\rm GL}_r(D)$, Amer. J. Math. 132 (2010), 1365–1396.Google Scholar
[BR07]Badulescu, A. I. and Renard, D., Zelevinsky involution and Moeglin–Waldspurger algorithm for ${\rm GL}_n(D)$, Funct. Anal. IX 48 (2007), 9–15.Google Scholar
[BZ76]Bernstein, I. N. and Zelevinsky, A. V., Representations of the group ${\rm GL}(n,F)$, where $F$ is a local non-Archimedean field, Uspehi Mat. Nauk 31 (1976), 5–70.Google Scholar
[BZ77]Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive $p$-adic groups. I, Ann. Sci. Éc. Norm. Supér 10 (1977), 441–472.Google Scholar
[CG97]Chriss, N. and Ginzburg, V., Representation theory and complex geometry (Birkhäuser, Boston, MA, 1997).Google Scholar
[Dat05]Dat, J.-F., $\nu $-tempered representations of $p$-adic groups, I: $l$-adic case, Duke Math. J. 126 (2005), 397–469.Google Scholar
[Dat09]Dat, J.-F., Finitude pour les représentations lisses de groupes $p$-adiques, J. Inst. Math. Jussieu 8 (2009), 261–333.CrossRefGoogle Scholar
[DKV84]Deligne, P., Kazhdan, D. and Vignéras, M.-F., Représentations des algèbres centrales simples $p$-adiques, in Representations of reductive groups over a local field (Travaux en Cours, Hermann, Paris, 1984), 33–117.Google Scholar
[Kat93]Kato, S.-I., Duality for representations of a Hecke algebra, Proc. Amer. Math. Soc. 119 (1993), 941–946.Google Scholar
[LTV99]Leclerc, B., Thibon, J.-Y. and Vasserot, E., Zelevinsky’s involution at roots of unity, J. Reine Angew. Math. 513 (1999), 33–51.CrossRefGoogle Scholar
[Min09]Mínguez, A., Sur l’irréductibilité d’une induite parabolique, J. Reine Angew. Math. 629 (2009), 107–131.Google Scholar
[MS12a]Mínguez, A. and Sécherre, V., Types modulo ℓ pour les formes intérieures de GLn sur un corps local non archimédien, Prépublication (2012).Google Scholar
[MS12b]Mínguez, A. and Sécherre, V., Représentations lisses modulo ℓ de GLm(D), Prépublication (2012).Google Scholar
[Rod82]Rodier, F., Représentations de ${\rm GL}(n,k)$ où $k$ est un corps $p$-adique, in Bourbaki seminar, Vol. 1981/1982, Astérisque, vol. 92 (Soc. Math. France, Paris, 1982), 201–218.Google Scholar
[Tad90]Tadić, M., Induced representations of ${\rm GL}(n,A)$ for $p$-adic division algebras $A$, J. Reine Angew. Math. 405 (1990), 48–77.Google Scholar
[Vig96]Vignéras, M.-F., Représentations l-modulaires d’un groupe réductif p-adique avec l≠p, Progress in Mathematics, vol. 137 (Birkhäuser, Boston, MA, 1996).Google Scholar
[Vig97]Vignéras, M.-F., Cohomology of sheaves on the building and $R$-representations, Invent. Math. 127 (1997), 349–373.Google Scholar
[Vig04]Vignéras, M.-F., On highest Whittaker models and integral structures, in Contributions to Automorphic forms, geometry and number theory: Shalikafest 2002 (Johns Hopkins University Press, 2004), 773–801.Google Scholar
[Zel80]Zelevinsky, A. V., Induced representations of reductive ${\mathfrak {p}}$-adic groups. II. On irreducible representations of ${\rm GL}(n)$, Ann. Sci. Éc. Norm. Supér. (4) 13 (1980), 165–210.Google Scholar