Article contents
Realization of GKM fibrations and new examples of Hamiltonian non-Kähler actions
Published online by Cambridge University Press: 24 August 2023
Abstract
We classify fibrations of abstract 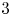 $3$-regular GKM graphs over
$3$-regular GKM graphs over 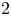 $2$-regular ones, and show that all fibrations satisfying the known necessary conditions for realizability are, in fact, realized as the projectivization of equivariant complex rank-
$2$-regular ones, and show that all fibrations satisfying the known necessary conditions for realizability are, in fact, realized as the projectivization of equivariant complex rank-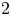 $2$ vector bundles over quasitoric
$2$ vector bundles over quasitoric 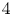 $4$-manifolds or
$4$-manifolds or 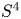 $S^4$. We investigate the existence of invariant (stable) almost complex, symplectic, and Kähler structures on the total space. In this way, we obtain infinitely many Kähler manifolds with Hamiltonian non-Kähler actions in dimension
$S^4$. We investigate the existence of invariant (stable) almost complex, symplectic, and Kähler structures on the total space. In this way, we obtain infinitely many Kähler manifolds with Hamiltonian non-Kähler actions in dimension 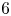 $6$ with prescribed one-skeleton, in particular with a prescribed number of isolated fixed points.
$6$ with prescribed one-skeleton, in particular with a prescribed number of isolated fixed points.
Keywords
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 2
- Cited by



