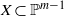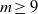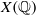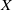Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Munshi, Ritabrata
2015.
Pairs of quadrics in 11 variables.
Compositio Mathematica,
Vol. 151,
Issue. 7,
p.
1189.
Browning, T. D.
and
Gorodnik, A.
2017.
Power-free values of polynomials on symmetric varieties.
Proceedings of the London Mathematical Society,
Vol. 114,
Issue. 6,
p.
1044.
Heath-Brown, D. R.
and
Pierce, L. B.
2017.
Simultaneous integer values of pairs of quadratic forms.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2017,
Issue. 727,
p.
85.
Munshi, Ritabrata
2018.
Geometry, Algebra, Number Theory, and Their Information Technology Applications.
Vol. 251,
Issue. ,
p.
273.
Browning, T.D.
and
Hu, L.Q.
2019.
Counting rational points on biquadratic hypersurfaces.
Advances in Mathematics,
Vol. 349,
Issue. ,
p.
920.
Mallesham, Kummari
2021.
On pairs of quadratic forms in five variables.
International Journal of Number Theory,
Vol. 17,
Issue. 09,
p.
2055.
Munshi, Ritabrata
2021.
Relative Trace Formulas.
p.
351.
Vishe, Pankaj
2023.
Rational points on complete intersections over Fq(t)${\mathbb {F}}_q(t)$.
Proceedings of the London Mathematical Society,
Vol. 126,
Issue. 2,
p.
556.
Bonolis, Dante
Browning, Tim
and
Huang, Zhizhong
2024.
Density of rational points on some quadric bundle threefolds.
Mathematische Annalen,
Vol. 390,
Issue. 3,
p.
4123.