Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-20T18:39:26.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Quotient closed subcategories of quiver representations

Part of: Representation theory of rings and algebras Algebraic combinatorics

Published online by Cambridge University Press:  15 October 2014

Steffen Oppermann ,
Idun Reiten  and
Hugh Thomas
Steffen Oppermann
Affiliation:
Department of Mathematics, NTNU, Trondheim, Norway email [email protected]
Idun Reiten
Affiliation:
Department of Mathematics, NTNU, Trondheim, Norway email [email protected]
Hugh Thomas
Affiliation:
Department of Mathematics and Statistics, UNB, PO Box 4400, Fredericton, Canada email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

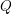Let $Q$ be a finite quiver without oriented cycles, and let 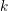$k$ be an algebraically closed field. The main result in this paper is that there is a natural bijection between the elements in the associated Weyl group 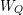$W_{Q}$ and the cofinite additive quotient closed subcategories of the category of finite dimensional right modules over 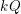$kQ$. We prove this correspondence by linking these subcategories to certain ideals in the preprojective algebra associated to 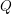$Q$, which are also indexed by elements of 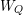$W_{Q}$.

Keywords

quotient closed subcategoriesWeyl groupspreprojective algebrassorting order

MSC classification

Primary: 16G20: Representations of quivers and partially ordered sets 16G70: Auslander-Reiten sequences (almost split sequences) and Auslander-Reiten quivers 05E10: Combinatorial aspects of representation theory
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 3 , March 2015 , pp. 568 - 602
Copyright
© The Author(s) 2014 

References

Amiot, C., Iyama, O., Reiten, I. and Todorov, G., Preprojective algebras and c-sortable words, Proc. Lond. Math. Soc. (3) 104 (2012), 513–539.Google Scholar
Armstrong, D., The sorting order on a Coxeter group, J. Combin. Th. Series A 116 (2009), 1285–1305.Google Scholar
Auslander, M., Platzeck, M. I. and Reiten, I., Coxeter functors without diagrams, Trans. Amer. Math. Soc. 250 (1979), 1–46.Google Scholar
Auslander, M. and Solberg, Ø., Relative homology and representation theory I-III, Comm. Algebra 21 (1993), 2995–3097.CrossRefGoogle Scholar
Baer, D., Geigle, W. and Lenzing, H., The preprojective algebra of a tame hereditary algebra, Comm. Algebra 15 (1987), 425–457.CrossRefGoogle Scholar
Baumann, P. and Kamnitzer, J., Preprojective algebras and MV polytopes, Represent. Theory 16 (2012), 152–188.CrossRefGoogle Scholar
Bernšteĭn, I. N., Gel’fand, I. M. and Ponomarev, V. A., Coxeter functors, and Gabriel’s theorem, Uspekhi Mat. Nauk 28 (1973), 19–33 (in Russian).Google Scholar
Björner, A. and Brenti, F., Combinatorics of Coxeter groups, Graduate Texts in Mathematics, vol. 231 (Springer, New York, 2005).Google Scholar
Buan, A. B., Iyama, O., Reiten, I. and Scott, J., Cluster structures for 2-Calabi–Yau categories and unipotent groups, Compositio Math. 145 (2009), 1035–1079.CrossRefGoogle Scholar
Cartan, H. and Eilenberg, S., Homological algebra (Princeton University Press, Princeton, NJ, 1956).Google Scholar
Deng, B., Du, J., Parshall, B. and Wang, J., Finite dimensional algebras and quantum groups, Mathematical Surveys and Monographs, vol. 150 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Geiß, Ch., Leclerc, B. and Schröer, J., Semicanonical bases and preprojective algebras. II. A multiplication formula, Compositio Math. 143 (2007), 1313–1334.Google Scholar
Ingalls, C. and Thomas, H., Noncrossing partitions and representations of quivers, Compositio Math. 145 (2009), 1533–1562.Google Scholar
Iyama, O. and Reiten, I., Fomin–Zelevinsky mutation and tilting modules over Calabi–Yau algebras, Amer. J. Math. 130 (2008), 1087–1149.Google Scholar
Krause, H. and Prest, M., The Gabriel–Roiter filtration of the Ziegler spectrum, Q. J. Math. 64 (2013), 891–901.Google Scholar
Lam, T. and Pylyavskyy, P., Total positivity for loop groups II: Chevalley generators, Transform. Groups 18 (2013), 179–231.CrossRefGoogle Scholar
Lam, T. and Williams, L., Total positivity for cominuscule Grassmannians, New York J. Math. 14 (2008), 53–99.Google Scholar
Pilaud, V. and Stump, C., Brick polytopes of spherical subword complexes: A new approach to generalized associahedra, Preprint (2011), arXiv:1111.3349.Google Scholar
Postnikov, A., Total positivity, Grassmannians, and networks, Preprint (2006),arXiv:math/0609764.Google Scholar
Reading, N., Clusters, Coxeter-sortable elements and noncrossing partitions, Trans. Amer. Math. Soc. 359 (2007), 5931–5958.CrossRefGoogle Scholar
Reading, N., Sortable elements and Cambrian lattices, Algebra Universalis 56 (2007), 411–437.Google Scholar
Ringel, C., The preprojective algebra of a quiver, in Algebras and Modules II, Can. Math. Soc. Conf. Proc., 24 (1998), 467–480.Google Scholar
Ringel, C., Minimal infinite submodule-closed subcategories, Bull. Sci. Math. 136 (2012), 820–830.Google Scholar
Stembridge, J., Folding by automorphisms, Preprint (2008); available at math.lsa.umich.edu/∼jrs/papers/folding.ps.gz.Google Scholar