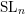Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T05:05:12.223Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantum K-theoretic geometric Satake: the $\operatorname{SL}_{n}$ case

Part of: Linear algebraic groups and related topics

Published online by Cambridge University Press:  30 October 2017

Sabin Cautis  and
Joel Kamnitzer
Sabin Cautis
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver BC, Canada email [email protected]
Joel Kamnitzer
Affiliation:
Department of Mathematics, University of Toronto, Toronto ON, Canada email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The geometric Satake correspondence gives an equivalence of categories between the representations of a semisimple group 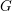$G$ and the spherical perverse sheaves on the affine Grassmannian 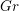$Gr$ of its Langlands dual group. Bezrukavnikov and Finkelberg developed a derived version of this equivalence which relates the derived category of 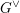$G^{\vee }$-equivariant constructible sheaves on 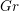$Gr$ with the category of 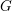$G$-equivariant 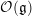${\mathcal{O}}(\mathfrak{g})$-modules. In this paper, we develop a K-theoretic version of the derived geometric Satake which involves the quantum group 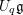$U_{q}\mathfrak{g}$. We define a convolution category 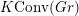$K\operatorname{Conv}(Gr)$ whose morphism spaces are given by the 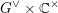$G^{\vee }\times \mathbb{C}^{\times }$-equivariant algebraic K-theory of certain fibre products. We conjecture that 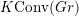$K\operatorname{Conv}(Gr)$ is equivalent to a full subcategory of the category of 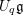$U_{q}\mathfrak{g}$-equivariant 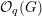${\mathcal{O}}_{q}(G)$-modules. We prove this conjecture when 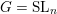$G=\operatorname{SL}_{n}$. A key tool in our proof is the 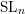$\operatorname{SL}_{n}$ spider, which is a combinatorial description of the category of 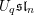$U_{q}\mathfrak{sl}_{n}$ representations. By applying horizontal trace, we show that the annular 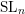$\operatorname{SL}_{n}$ spider describes the category of 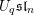$U_{q}\mathfrak{sl}_{n}$-equivariant 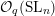${\mathcal{O}}_{q}(\operatorname{SL}_{n})$-modules. Then we use quantum loop algebras to relate the annular 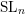$\operatorname{SL}_{n}$ spider to 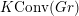$K\operatorname{Conv}(Gr)$. This gives a combinatorial/diagrammatic description of both categories and proves our conjecture.

Keywords

geometric Satake correspondencequantum groupsaffine spiderswebscategorification

MSC classification

Primary: 20G42: Quantum groups (quantized function algebras) and their representations
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 2 , February 2018 , pp. 275 - 327
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bakalov, B. and Kirillov, A., Lectures on tensor categories and modular functors (American Mathematical Society, Providence, RI, 2001).Google Scholar
Beck, J. and Nakajima, H., Crystal bases and two-sided cells of quantum affine algebras , Duke Math. J. 123 (2004), 335–402.Google Scholar
Beliakova, A., Habiro, K., Lauda, A. and Zivković, M., Trace decategorification of categorified quantum sl2 , Math. Ann. 367 (2017), 397–440.Google Scholar
Ben-Zvi, D., Brochier, A. and Jordan, D., Integrating quantum groups over surfaces: quantum character varieties and topological field theory, Preprint (2015), arXiv:1501.04652.Google Scholar
Berenstein, A. and Zwicknagl, S., Braided symmetric and exterior algebras , Trans. Amer. Math. Soc. 360 (2008), 3429–3472.Google Scholar
Bezrukavnikov, R. and Finkelberg, M., Equivariant Satake category and Kostant–Whittaker reduction , Mosc. Math. J. 8 (2008), 39–72.Google Scholar
Cautis, S., Clasp technology to knot homology via the affine Grassmannian , Math. Ann. 363 (2015), 1053–1115.Google Scholar
Cautis, S. and Kamnitzer, J., Knot homology via derived categories of coherent sheaves I, sl2 case , Duke Math. J. 142 (2008), 511–588.Google Scholar
Cautis, S. and Kamnitzer, J., Knot homology via derived categories of coherent sheaves II, sl m case , Invent. Math. 174 (2008), 165–232.Google Scholar
Cautis, S. and Kamnitzer, J., Knot homology via derived categories of coherent sheaves IV, coloured links , Quantum Topol. 8 (2017), 381–411.Google Scholar
Cautis, S., Kamnitzer, J. and Licata, A., Categorical geometric skew Howe duality , Invent. Math. 180 (2010), 111–159.CrossRefGoogle Scholar
Cautis, S., Kamnitzer, J. and Morrison, S., Webs and quantum skew Howe duality , Math. Ann. 360 (2014), 351–390.Google Scholar
Chriss, N. and Ginzburg, V., Representation theory and complex geometry (Birkhäuser, Boston, MA, 1997).Google Scholar
Doty, S. and Green, R., Presenting affine q-Schur algebras , Math. Z. 256 (2007), 311–345.Google Scholar
Elias, B., Light ladders and clasp conjectures, Preprint (2015), arXiv:1510.06840.Google Scholar
Elias, B., Quantum Satake in type A: Part I , J. Comb. Algebra 1 (2017), 63–125.Google Scholar
Fontaine, B., Kamnitzer, J. and Kuperberg, G., Buildings, spiders, and geometric Satake , Compos. Math. 149 (2013), 1871–1912.Google Scholar
Gaitsgory, D., Twisted Whittaker model and factorizable sheaves , Selecta Math. (N.S.) 13 (2008), 617–659.CrossRefGoogle Scholar
Green, R., The affine q-Schur algebra , J. Algebra 215 (1999), 379–411.Google Scholar
Grigsby, J., Licata, A. and Wehrli, S., Annular Khovanov homology and knotted Schur–Weyl representations, Preprint (2015), arXiv:1505.04386.Google Scholar
Haines, T., Equidimensionality of convolution morphisms and applications to saturation problems , Adv. Math. 207 (2006), 297–327.CrossRefGoogle Scholar
Jordan, D., Quantized multiplicative quiver varieties , Adv. Math. 250 (2014), 420–446.Google Scholar
Kapustin, A. and Witten, E., Electric–magnetic duality and the geometric Langlands program , Commun. Number Theory Phys. 1 (2007), 1–236.Google Scholar
Kazhdan, D. and Lusztig, G., Proof of the Deligne–Langlands conjecture for Hecke algebras , Invent. Math. 87 (1987), 153–215.Google Scholar
Khovanov, M., sl3 link homology , Algebr. Geom. Topol. 4 (2004), 1045–1081.Google Scholar
Kraft, H. and Procesi, C., Closures of conjugacy classes of matrices , Invent. Math. 53 (1979), 227–247.Google Scholar
Lusztig, G., Introduction to quantum groups, Progress in Mathematics, vol. 110 (Birkhäuser Boston, Boston, MA, 1993).Google Scholar
Lyubashenko, V. and Majid, S., Braided groups and quantum Fourier transform , J. Algebra 166 (1994), 506–528.Google Scholar
McGerty, K., Generalized q-Schur algebras and quantum Frobenius , Adv. Math. 214 (2007), 116–131.Google Scholar
Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings , Ann. of Math. (2) 166 (2007), 95–143.Google Scholar
Mirković, I. and Vybornov, M., On quiver varieties and affine Grassmannians of type A , C. R. Math. Acad. Sci. Paris 336 (2003), 207–212.Google Scholar
Nakajima, H., Quiver varieties and finite-dimensional representations of quantum affine algebras , J. Amer. Math. Soc. 14 (2001), 145–238.Google Scholar
Ngo, B. C., Faisceaux pervers, homomorphisme de changement de base et lemme fondamental de Jacquet et Ye , Ann. Sci. Éc. Norm. Supér. (4) 32 (1999), 619–679.Google Scholar
Queffelec, H., Skein modules from skew Howe duality and affine extensions , SIGMA Symmetry Integrability Geom. Methods Appl. 11 (2015), 030, 36 pp.Google Scholar
Queffelec, H. and Rose, D., Sutured annular Khovanov–Rozansky homology, Preprint (2015), arXiv:1506.08188.Google Scholar
Queffelec, H. and Rose, D., The sl n foam 2-category: a combinatorial formulation of Khovanov–Rozansky homology via categorical skew Howe duality , Adv. Math. 302 (2016), 1251–1339.Google Scholar
Sevostyanov, A., Quantum deformation of Whittaker modules and the Toda lattice , Duke Math. J. 105 (2000), 211–238.Google Scholar
Thomason, R. W., Algebraic K-theory of group scheme actions , in Algebraic topology and algebraic K-theory (Princeton, NJ, 1983), Annals of Mathematics Studies, vol. 113 (Princeton University Press, Princeton, NJ, 1987), 539–563.Google Scholar
Thomason, R. W., Lefschetz–Riemann–Roch theorem and coherent trace formula , Invent. Math. 85 (1986), 515–543.CrossRefGoogle Scholar
Walker, K., TQFTs (2006), http://canyon23.net/math/tc.pdf.Google Scholar
Zhu, X., An introduction to affine Grassmannians and the geometric Satake equivalence, Preprint (2016), arXiv:1603.05593.Google Scholar