Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T05:12:16.988Z Has data issue: false hasContentIssue false
  • English
  • Français

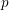The pro-$p$-Iwahori Hecke algebra of a reductive 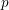$p$-adic group I

Part of: Forms and linear algebraic groups Linear algebraic groups and related topics Representation theory of groups

Published online by Cambridge University Press:  23 October 2015

Marie-France Vigneras
Marie-France Vigneras*
Affiliation:
Institut de Mathematiques de Jussieu, 175 rue du Chevaleret, Paris 75013, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

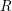Let $R$ be a commutative ring, let 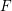$F$ be a locally compact non-archimedean field of finite residual field 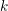$k$ of characteristic 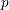$p$, and let 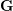$\mathbf{G}$ be a connected reductive 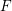$F$-group. We show that the pro-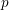$p$-Iwahori Hecke 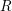$R$-algebra of 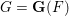$G=\mathbf{G}(F)$ admits a presentation similar to the Iwahori–Matsumoto presentation of the Iwahori Hecke algebra of a Chevalley group, and alcove walk bases satisfying Bernstein relations. This was previously known only for a 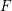$F$-split group 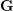$\mathbf{G}$.

Keywords

pro-p-Iwahori Hecke algebraaffine Hecke algebraIwahori Weyl groupreductive p-adic groupparahoric subgroupsalcove walk

MSC classification

Primary: 11E95: $p$-adic theory 20G25: Linear algebraic groups over local fields and their integers 20C08: Hecke algebras and their representations
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 4 , April 2016 , pp. 693 - 753
Copyright
© The Author 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, N., Henniart, G., Herzig, F. and Vigneras, M.-F., A classification of irreducible admissible modulo $p$representations of $p$-adic reductive groups, Preprint (2014), arXiv:1412.0737.Google Scholar
Borel, A., Admissible representations of a semi-simple group over a local field with vectors fixed under an Iwahori subgroup, Invent. Math. 35 (1976), 233–259.Google Scholar
Borel, A., Linear algebraic groups, second enlarged edition (Springer, New York, 1991).CrossRefGoogle Scholar
Borel, A. and Tits, J., Groupes réductifs, Publ. Math. Inst. Hautes Études Sci. 27 (1965), 55–151.Google Scholar
Bourbaki, N., Groupes et algèbres de Lie, chapitres 4, 5 et 6 (Hermann, Paris, 1968).Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local. I. Données radicielles valuées, Publ. Math. Inst. Hautes Études Sci. 41 (1972), 5–252.Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local. II Schémas en groupes. Existence d’une donnée radicielle valuées, Publ. Math. Inst. Hautes Études Sci. 60 (1984), 197–376; part II.Google Scholar
Cabanes, M. and Enguehard, M., Representation theory of finite reductive groups (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Görtz, U., Alcove walks and nearby cycle on affine flag manifolds, J. Algebraic Combin. 26 (2007), 415–430.Google Scholar
Haines, H. and Rapoport, M., Appendix: On parahoric subgroups, Adv. Math. 219 (2008), 188–198; appendix to: G. Pappas and M. Rapoport, Twisted loop groups and their affine flag varieties, Adv. Math. 219 (2008), 118–198.CrossRefGoogle Scholar
Haines, T. and Rostami, S., The Satake isomorphism for special maximal parahoric algebras, Represent. Theory 14 (2010), 264–284.Google Scholar
Henniart, G. and Vigneras, M.-F., A Satake isomorphism for representations modulo p of reductive groups over local fields, J. Reine Angew. Math. 701 (2015), 33–75.Google Scholar
Iwahori, N. and Matsumoto, H., On some Bruhat decomposition and the structure of the Hecke ring of p-adic Chevalley groups, Publ. Math. Inst. Hautes Études Sci. 25 (1965), 5–48.Google Scholar
Kottwitz, R., Isocrystals with additional structure II, Compositio Math. 109 (1997), 225–339.Google Scholar
Koziol, K. and Xu, P., Hecke modules and supersingular representations of U (2, 1), Represent. Theory 19 (2015), 56–93.Google Scholar
Kumar, S., Kac–Moody groups, their flag varieties and representation theory, Progress in Mathematics, vol. 204 (Birkhäuser, Boston, 2002).Google Scholar
Lusztig, G., Affine Hecke algebras and their graded version, J. Amer. Math. Soc. 2 (1989), 599–635.Google Scholar
Milne, J. S. and Shih, K. Y., Conjugates of Shimura varieties, in Hodge cycles, motives, and Shimura varieties, Lecture Notes in Mathematics, vol. 900 (Springer, Berlin, 1981).Google Scholar
Richarz, T., On the Iwahori–Weyl group, Preprint (2013), arXiv:1310.4635.Google Scholar
Schmidt, N. A., Generische pro-p-algebren (Dilpomarbeit, Berlin, 2009).Google Scholar
Schneider, P. and Stuhler, U., Representation theory and sheaves on the Bruhat–Tits building, Publ. Math. Inst. Hautes Études Sci. 85 (1997), 97–191.Google Scholar
Steinberg, R., Lecture on Chevalley groups, Yale notes (1967).Google Scholar
Vigneras, M.-F., Représentations ℓ-modulaires d’un groupe réductif p-adique avec ℓ≠p, Progress in Mathematics, vol. 137 (Birkhäuser, Boston, 1996).Google Scholar
Vigneras, M.-F., Pro-p-Iwahori Hecke algebra and supersingular Fp -representations, Math. Ann. 331 (2005), 523–556; Erratum, Math. Ann. 333 (2005), 699–701.CrossRefGoogle Scholar
Vigneras, M.-F., Algèbres de Hecke affines génériques, Represent. Theory 10 (2006), 1–20.Google Scholar