Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T05:35:49.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Proof of de Smit’s conjecture: a freeness criterion

Part of: Algebraic geometry: Foundations Discontinuous groups and automorphic forms Theory of modules and ideals

Published online by Cambridge University Press:  14 August 2017

Sylvain Brochard
Sylvain Brochard*
Affiliation:
Institut Montpelliérain Alexander Grothendieck, CNRS, Université de Montpellier, Place Eugène Bataillon CC051, 34 095 Montpellier CEDEX 5, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

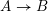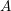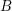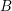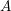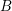Let $A\rightarrow B$ be a morphism of Artin local rings with the same embedding dimension. We prove that any $A$ -flat $B$ -module is $B$ -flat. This freeness criterion was conjectured by de Smit in 1997 and improves Diamond’s criterion [The Taylor–Wiles construction and multiplicity one, Invent. Math. 128 (1997), 379–391, Theorem 2.1]. We also prove that if there is a nonzero $A$ -flat $B$ -module, then 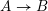$A\rightarrow B$ is flat and is a relative complete intersection. Then we explain how this result allows one to simplify Wiles’s proof of Fermat’s last theorem: we do not need the so-called ‘Taylor–Wiles systems’ any more.

Keywords

flatnessArtin local ringsembedding dimensionpatching

MSC classification

Primary: 13C10: Projective and free modules and ideals 11F80: Galois representations 14A05: Relevant commutative algebra
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 11 , November 2017 , pp. 2310 - 2317
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Böckle, G. and Khare, C., Mod l representations of arithmetic fundamental groups. II. A conjecture of A. J. de Jong , Compos. Math. 142 (2006), 271–294.Google Scholar
Bourbaki, N., Éléments de mathématique. Algèbre commutative (Springer, Berlin, 2006), chs 1–4. Reprint of the 1985 original.Google Scholar
Breuil, C. and Diamond, F., Formes modulaires de Hilbert modulo p et valeurs d’extensions entre caractères galoisiens , Ann. Sci. Éc. Norm. Supér. (4) 47 (2014), 905–974.Google Scholar
Brochard, S. and Mézard, A., About De Smit’s conjecture on flatness , Math. Z. 267 (2011), 385–401.Google Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations , Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181, with Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras.Google Scholar
Conrad, B., Diamond, F. and Taylor, R., Modularity of certain potentially Barsotti–Tate Galois representations , J. Amer. Math. Soc. 12 (1999), 521–567.Google Scholar
Darmon, H., Diamond, F. and Taylor, R., Fermat’s last theorem , in Elliptic curves, modular forms & Fermat’s last theorem (Hong Kong, 1993) (International Press, Cambridge, MA, 1997), 2–140.Google Scholar
Diamond, F., The Taylor–Wiles construction and multiplicity one , Invent. Math. 128 (1997), 379–391.CrossRefGoogle Scholar
Dickinson, M., On the modularity of certain 2-adic Galois representations , Duke Math. J. 109 (2001), 319–382.Google Scholar
Dimitrov, M., On Ihara’s lemma for Hilbert modular varieties , Compos. Math. 145 (2009), 1114–1146.Google Scholar
Emerton, M., Gee, T. and Savitt, D., Lattices in the cohomology of Shimura curves , Invent. Math. 200 (2015), 1–96.Google Scholar
Genestier, A. and Tilouine, J., Systèmes de Taylor–Wiles pour GSp 4 , in Formes automorphes. II. Le cas du groupe GSp (4), Astérisque, vol. 302 (Société Mathématique de France, 2005), 177–290.Google Scholar
Harris, M., The Taylor–Wiles method for coherent cohomology , J. reine angew. Math. 679 (2013), 125–153.Google Scholar
Khare, C. and Wintenberger, J.-P., Serre’s modularity conjecture II , Invent. Math. 178 (2009), 505–586.Google Scholar
Kisin, M., The Fontaine–Mazur conjecture for GL2 , J. Amer. Math. Soc. 22 (2009), 641–690.Google Scholar
Kisin, M., Modularity of 2-adic Barsotti–Tate representations , Invent. Math. 178 (2009), 587–634.Google Scholar
Kisin, M., Moduli of finite flat group schemes, and modularity , Ann. of Math. (2) 170 (2009), 1085–1180.Google Scholar
Pilloni, V., Modularité, formes de Siegel et surfaces abéliennes , J. reine angew. Math. 666 (2012), 35–82.Google Scholar
Simon, A.-M. and Strooker, J., Complete intersections of dimension zero: variations on a theme of Wiebe, Preprint (2006), arXiv:0703880.Google Scholar
Taylor, R., On the meromorphic continuation of degree two L-functions , Doc. Math. Extra Vol. (2006), 729–779; electronic.Google Scholar