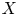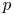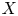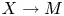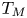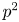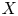Projective varieties with nef tangent bundle in positive characteristic

Abstract

Let $X$ be a smooth projective variety defined over an algebraically closed field of positive characteristic $p$ whose tangent bundle is nef. We prove that $X$ admits a smooth morphism $X \to M$ such that the fibers are Fano varieties with nef tangent bundle and $T_M$ is numerically flat. We also prove that extremal contractions exist as smooth morphisms. As an application, we prove that, if the Frobenius morphism can be lifted modulo $p^2$, then $X$ admits, up to a finite étale Galois cover, a smooth morphism onto an ordinary abelian variety whose fibers are products of projective spaces.

1. Introduction

1.1 Positivity of tangent bundles

Mori's celebrated proof of the Hartshorne conjecture asserts that a smooth projective variety $X$ over an arbitrary algebraically closed field is isomorphic to a projective space $\mathbb {P}^n$ if and only if the tangent bundle satisfies the positivity condition called ample [Mor79]. This characterization of projective spaces is the algebro-geometric counterpart of the Frankel conjecture in complex geometry, which was proved by [SY80].

As an attempt to generalize this kind of characterization, Campana and Peternell started the study of complex projective varieties satisfying a numerical semipositivity condition, called nef (see § 2 for the definition). Philosophically, if the tangent bundle is semipositive, then the variety is expected to decompose into the ‘positive’ part and the ‘flat’ part. Indeed, after the series of papers by Campana and Peternell [CP91, CP93], this type of decomposition has been accomplished by Demailly, Peternell, and Schneider.

Theorem 1.1 ([DPS94, Main theorem], $/\mathbb {C}$)

If the tangent bundle of a complex projective manifold $X$ is nef, then, up to an étale cover, the variety $X$ admits a fibration over an abelian variety whose fibers $F$ are Fano varieties (varieties with ample anti-canonical divisor $-K_F$).

This decomposition theorem reduces the study of varieties with nef tangent bundles to that of Fano varieties. Campana and Peternell conjectured that Fano varieties with nef tangent bundles are rational homogeneous varieties $G/P$, where $G$ is a semisimple algebraic group and $P$ is a parabolic group [CP91, 11.2].

Main tools to study Fano varieties are the theory of rational curves and Mori's theory of extremal rays. From the view point of Mori's theory, rational homogeneous spaces $G/P$ share an important feature that their contractions are always smooth. In the same paper [DPS94], Demailly, Peternell, and Schneider also proved the following fundamental structure theorem.

Theorem 1.2 ([DPS94, Theorem 5.2] and [SW04, Theorem 4.4], $/\mathbb {C}$)

Let $X$ be a smooth complex projective variety and assume that $T_X$ is nef. Then any $K_X$-negative extremal contraction $f \colon X \to Y$ is smooth.

This theorem provides an evidence for the validity of the Campana–Peternell conjecture. In fact, it plays an important role in the course of partial proofs of the Campana–Peternell conjecture [CP91, CP93, Mok02, Hwa06, Wat14, Wat15, Kan16, Kan17, MOSW15, SW04]. We also refer the reader to [MOSW⁺15] for an account of the Campana–Peternell conjecture.

The purpose of this paper is to establish the analogous results for varieties with nef tangent bundle in positive characteristic. Note that the proofs in [DPS94] depend on analytic arguments, which we cannot directly apply in positive characteristic case (for details, see § 1.7). Thus, we will take a different strategy based on the Mori theory. The rough idea is to use an analogue of Theorem 1.2 to obtain the decomposition theorem: by taking successive extremal contractions, each of which is a smooth morphism, we find a smooth morphism $\varphi : X \to M$ such that $T_{M}$ is numerically flat and any fiber of $\varphi$ is rationally chain connected (RCC). Then, by proving that the fibers of $\varphi$ are Fano varieties, we obtain our decomposition theorem. Thus, the key step is to give a characterization of Fano varieties with nef tangent bundles or, more precisely, to study varieties with nef tangent bundle which contain many rational curves.

In the rest of this section, unless otherwise stated, $k$ denotes an algebraically closed field of positive characteristic $p >0$, and $X$ is a smooth projective variety defined over $k$.

1.2 Rational curves on varieties with nef tangent bundle

Recall that a Fano variety $X$ is RCC (see [Mor79, Theorem 5], [Cam92], and [KMM92a, Theorem 3.3]). In characteristic zero, rational chain connectedness of $X$, in turn, implies that there exists a highly unobstructed rational curve $\mathbb {P}^1 \to X$ called very free rational curve, whose existence is equivalent to a stronger rational connectedness notion, that $X$ is separably rationally connected (SRC) [KMM92b, Theorem 2.1] (see also Definition 3.1).

The first theorem of this article asserts that, if $T_X$ is nef, then the same also holds in positive characteristic.

Theorem 1.3 (RCC $\implies$ SRC)

Let $X$ be a smooth projective variety over $k$ and assume that $T_X$ is nef. If $X$ is RCC, then $X$ is SRC.

Thus, if $X$ is RCC, then $X$ contains a very free rational curve. By [Deb03, Corollaire 3.6], [She10, Corollary 5.3], [BD13], and [Gou14], we have the next corollary.

Corollary 1.4 Let $X$ be a smooth projective variety over $k$ and assume that $T_X$ is nef. If $X$ is RCC, then the following hold:

1. (1) $X$ is algebraically simply connected, i.e. any connected finite étale cover of $X$ is trivial;

2. (2) $H^1(X, \mathcal {O}_X) = 0$;

3. (3) every numerically flat vector bundle on $X$ is trivial.

1.3 Contractions of extremal rays

Recall that, over an arbitrary algebraically closed field $k$, Mori's cone theorem holds [Mor82]. Namely, the Kleiman–Mori cone $\overline {\operatorname {NE}} (X)$ is locally polyhedral in $K_X$-negative side and, thus, it decomposes as follows:

\[ \overline{\operatorname{NE}}(X) = \overline{\operatorname{NE}} _{K_X \geq 0} + \sum R_{i}, \]

where $R_i = \mathbb {R}_{\geq 0}[C_i]$ are $K_X$-negative extremal rays, each of which is spanned by a class of a rational curve $C_i$. Note that, in characteristic zero, each extremal ray is realized in a geometrical way, i.e. there exists the contraction of each extremal ray $R$ (see, e.g., [KM98]), while the existence of extremal contractions is widely open in positive characteristic. The following theorem asserts that, if $T_X$ is nef, then the contraction of an extremal ray exists and, in fact, it is smooth.

Theorem 1.5 (Existence and smoothness of contractions)

Let $X$ be a smooth projective variety over $k$ and assume that $T_X$ is nef.

Let $R \subset \overline {\operatorname {NE}} (X)$ be a $K_X$-negative extremal ray. Then the contraction $f \colon X \to Y$ of $R$ exists and the following hold:

1. (1) $f$ is smooth;

2. (2) any fiber $F$ of $f$ is an SRC Fano variety with nef tangent bundle;

3. (3) $T_Y$ is again nef.

See also Corollary 6.1 for contractions of extremal faces.

1.4 Decomposition theorem

To prove the decomposition theorem, we first construct a smooth morphism $X \to M$ whose fibers are RCC and image $M$ has numerically flat tangent bundle $T_M$. The following theorem ensures that the fibers are Fano varieties.

Theorem 1.6 (RCC $\implies$ Fano)

Let $X$ be a smooth projective variety over $k$ and assume that $T_X$ is nef. If $X$ is RCC, then $X$ is a smooth Fano variety. Moreover, the Kleiman–Mori cone $\operatorname {NE}(X)$ of $X$ is simplicial.

Remark 1.7 In fact, the above assertion also holds in relative settings (see Theorem 5.3).

By combining the above theorems we can obtain the decomposition theorem of varieties with nef tangent bundle.

Theorem 1.8 (Decomposition theorem)

Let $X$ be a smooth projective variety over $k$ and assume that $T_X$ is nef. Then $X$ admits a smooth contraction $\varphi \colon X \to M$ such that:

1. (1) any fiber of $\varphi$ is a smooth SRC Fano variety with nef tangent bundle;

2. (2) $T_M$ is numerically flat.

Remark 1.9 Since there are no rational curves on varieties with numerically flat tangent bundles, the morphism $\varphi$ is the maximally rationally chain connected (MRCC) fibration in the sense of [Kol96, Chapter IV, § 5].

1.5 Questions

The above decomposition theorem reduces the study of varieties with nef tangent bundle to two cases (the Fano case and the $K_X$-trivial case). The following suggests the possible structures of varieties in these two cases.

Question 1.10 ([CP91, Conjecture 11.1], [Wat17, Question 1])

Let $X$ be a smooth projective variety over $k$ and assume $T_X$ is nef.

1. (1) If $X$ is a Fano variety, then is $X$ a homogeneous space $G/P$, where $G$ is a semisimple algebraic group and $P$ is a parabolic subgroup?

2. (2) If $K_X \equiv 0$ or, equivalently, $T_X$ is numerically flat, then is $X$ an étale quotient of an abelian variety?

Note that, in characteristic zero, the second assertion is true by virtue of the Beauville–Bogomolov–Yau decomposition, which is studied intensively in characteristic positive [PZ20], but is still open. See also [MS87, Li10, Lan15, Wat17, Jos21] for partial answers and related topics on the above question.

1.6 Application

In the last part of this paper, we will apply our results to the study of $F$-liftable varieties. A smooth projective variety $X$ (over an algebraically closed field of positive characteristic) is said to be $F$-liftable, if it lifts modulo $p^2$ with the Frobenius morphism (see Definition 7.1 for the precise definition). The known examples of $F$-liftable varieties are toric varieties and ordinary abelian varieties. Conversely, any $F$-liftable variety is expected to decompose into these two types of varieties.

Conjecture 1.11 [AWZ21, Conjecture 1]

Let $Z$ be an $F$-liftable variety. Then there exists a finite Galois cover $f \colon Y \to Z$ such that the Albanese morphism $\alpha _{Y} \colon Y \to \operatorname {Alb} (Y)$ is a toric fibration.

This conjecture is confirmed only in the case of homogeneous varieties [BTLM97, AWZ21]. In fact, in [AWZ21, Proposition 6.3.2], the conjecture is verified when $X$ is a Fano manifold with nef tangent bundle whose Picard number is one. Here we apply our study to show that the conjecture holds under a more general situation that $T_X$ is nef.

Theorem 1.12 ($F$-liftable varieties with nef tangent bundle)

If $X$ is $F$-liftable and $T_X$ is nef, then there exists a finite étale Galois cover $f \colon Y \to X$ such that the Albanese morphism $\alpha _{Y} \colon Y \to \operatorname {Alb} (Y)$ is a smooth morphism onto an ordinary abelian variety whose fibers are products of projective spaces.

1.7 Differences between our proofs and proofs in complex analytic case

Here we summarize major differences between our proofs and the proofs in [DPS94].

At first, we review the proof of Theorem 1.1 (which is [DPS94, Main theorem]). Let $X$ be a smooth projective variety over $\mathbb {C}$ and assume that $T_X$ is nef. In the course of their study, Demailly, Peternell, and Schneider first proved the following assertions [DPS94, Proposition 3.9 and Proposition 3.10] (see also [CP91, Proposition 2.4]).

1. (1) The Albanese map $X \to \operatorname {Alb}(X)$ is a smooth morphism.

2. (2) If $(-K_X)^{\dim X}>0$, then $X$ is a Fano variety.

3. (3) If $(-K_X)^{\dim X}=0$, then there exists a finite étale cover of $X$ whose irregularity is positive.

Then, by repeatedly applying these assertions, they find an appropriate étale cover of $X$ whose Albanese map decomposes $X$ into Fano part and abelian part. Note that the proof of the above assertions heavily relies on three analytic ingredients (the complex analytic description of the Albanese maps, the Kodaira vanishing theorem, and the Hodge theory), which fail in positive characteristic. Note also that the conclusion of Theorem 1.1 immediately implies that varieties with numerically flat tangent bundle are étale quotients of abelian varieties, while this characterization is still unknown in positive characteristic (see Question 1.10).

In positive characteristic, we will take the Mori theoretic view point, and obtain the decomposition theorem (Theorem 1.8) by proving the following assertions:

• – characterization of Fano varieties with nef tangent bundles (Theorems 1.3 and 1.6; Fano $\iff$ SRC $\iff$ RCC);

• – existence and smoothness of contractions (Theorem 1.5).

Our proof is sketched as follows: By taking successive $K$-negative contractions of extremal rays (each of which is a smooth morphism, thanks to Theorem 1.5), we find a smooth morphism $\varphi : X \to M$ such that $T_{M}$ is numerically flat and any fiber of $\varphi$ is RCC. Then, by applying the characterization of Fano varieties, we obtain our decomposition theorem. The most essential part of our approach is to prove Theorem 1.3 (RCC $\implies$ SRC), which is used in both proofs of Theorem 1.5 (existence and smoothness of contractions) and Theorem 1.6 (RCC $\implies$ Fano).

1.8 Outline of the paper

This article is organized as follows. In § 2, we provide a preliminaries on nef vector bundles.

In § 3, we study the SRC varieties with nef tangent bundle and prove Theorem 1.3. The main ingredient of the proof is Shen's theorem that provides a relation between being SRC and foliations in positive characteristic [She10]. By using this relation, we construct a purely inseparable finite morphism $X \to Y$ (if $X$ is RCC) such that $Y$ also has nef tangent bundle and is SRC. From this morphism $X \to Y$, we can construct an action of the group scheme $G = \mu _p$ or $\alpha _p$ on $Y$ without fixed points. Then, by following Kollár's proof of simple connectedness of SRC varieties [Deb03, Corollaire 3.6], we will have a contradiction and, hence, $X$ itself is SRC.

In § 4, we study extremal contractions on varieties with nef tangent bundle and prove Theorem 1.5. Theorem 1.5 essentially follows from the arguments of [Kan22, Theorem 2.2] and [SW04, Lemma 4.12], while we use Theorem 1.3 to adapt these arguments in the positive characteristic case.

In § 5, we will prove Theorem 1.6. In fact, we will study the relative Kleiman–Mori cone $\operatorname {NE} (X/Y)$ of a contraction $f \colon X \to Y$ with RCC fibers. The main theorem of this section is Theorem 5.3, which proves that the cone $\operatorname {NE} (X/Y)$ is simplicial cone spanned by $K_X$-negative extremal rays. The proof essentially goes the same way as that of [Wat21, Proof of Theorem 4.16].

In § 6, we prove Theorem 1.8, which easily follows from the theorems in previous sections.

In the last section, we study the case where $X$ is $F$-liftable and prove Theorem 1.12.

1.9 Conventions

Throughout this paper, we work over an algebraically closed field $k$ of characteristic $p>0$. We use standard notation and conventions as in [Har77], [Kol96], [KM98], and [Deb01].

• – Unless otherwise stated, a point means a closed point and a fiber means a fiber over a closed point.

• – A rational curve on a variety $X$ is a nonconstant morphism $f \colon \mathbb {P}^1 \to X$ or, by an abuse of notation, its image $f(\mathbb {P}^1) \subset X$.

• – A contraction $f \colon X \to Y$ is a projective morphism of varieties such that $f_* \mathcal {O}_X =\mathcal {O} _Y$.

• – For a contraction $f \colon X \to Y$, we denote by $N_1(X / Y)$ the $\mathbb {R}$-vector space of the numerical equivalence classes of relative $1$-cycles. The cone of relative effective $1$-cycles $\operatorname {NE} (X/Y) \subset N_1(X/Y)$ is the semi-subgroup generated by the classes of effective $1$-cycles. The closure $\overline {\operatorname {NE}}(X/Y)$ is called the relative Kleiman–Mori cone.

• – For a contraction $X \to Y$, the relative Picard number $\rho (X /Y)$ is the rank of $N_1(X/Y)$.

• – For a contraction $f \colon X \to Y$, $N^1(X/Y)$ is the $\mathbb {R}$-vector space generated by the $f$-numerical equivalence classes of Cartier divisors. Note that $N^1(X/Y)$ and $N_1(X/Y)$ are finite-dimensional vector spaces, which are dual to each other.

• – If $Y =\operatorname {Spec} k$, then we will use $N_1(X)$, $\operatorname {NE}(X)$, $\rho (X)$, and $N^1(X)$ instead of $N_1(X/Y)$, $\operatorname {NE}(X/Y)$, $\rho (X/Y)$, and $N^1(X/Y)$.

• – For a smooth projective variety $S$, a smooth $S$-fibration is a smooth morphism between varieties whose closed fibers are isomorphic to $S$.

• – The dual vector bundle of a vector bundle $\mathcal {E}$ is $\mathcal {E}^{\vee }$.

• – The Grothendieck projectivization $\operatorname {Proj}(\operatorname {Sym} \mathcal {E})$ of a vector bundle $\mathcal {E}$ is $\mathbb {P}(\mathcal {E})$.

• – A subsheaf $\mathcal {F} \subset \mathcal {E}$ of a locally free sheaf $\mathcal {E}$ is called a subbundle if the quotient bundle $\mathcal {E}/\mathcal {F}$ is a locally free sheaf.

• – For a projective variety $X$, we denote by $F_X$ the absolute Frobenius morphism $X \to X$.

Note that a contraction, if it exists, is uniquely determined by $\operatorname {NE} (X/Y) \subset N_1(X)$. A contraction of a $K_X$-negative extremal ray $R$ is, by definition, a contraction $f \colon X \to Y$ such that $\rho (X/Y) = 1$ and $R := \operatorname {NE}(X/Y) \subset N_1(X/Y)_{K_X \leq 0}$.

Furthermore, we use standard terminology on families of rational curves. For example,

• – $\operatorname {RatCurves}^{\rm n} (X)$ is (the normalization of) the scheme that parametrizes rational curves on X, and a family of rational curves is an irreducible component $\mathcal {M}$ of the scheme $\operatorname {RatCurves}^{\rm n} (X)$ (the superscript ‘${\rm n}$’ means that the parameter space is normalized, see [Kol96, Chapter II. Definition 2.12]).

• – For a family $\mathcal {M}$ of rational curves, there exists the diagram

  
  where:

  1. ∗ $p$ is a smooth $\mathbb {P}^1$-fibration, which corresponds to the universal family;

  2. ∗ $q$ is the evaluation map.

  Thus, a point $m \in \mathcal {M}$ corresponds to a rational curve $q|_{p^{-1}(m)} \colon p^{-1}(m) \simeq \mathbb {P}^1 \to X$.

• – A family $\mathcal {M}$ of rational curves is called unsplit if it is projective.

For the details of the constructions of these spaces and for basic properties, we refer the reader to [Kol96, Chapter II, § 2] and also to [Mor79].

2. Preliminaries on nef vector bundles

We collect some facts on nef vector bundles.

Let $\mathcal {E}$ be a vector bundle on a smooth projective variety $X$. Then the bundle $\mathcal {E}$ is called nef if the relative tautological divisor $\mathcal {O}_{\mathbb {P}(\mathcal {E})}(1)$ is nef. By the definition, any quotient bundle of a nef vector bundle is again nef. In addition, for a morphism $f \colon Y \to X$ from a projective variety $Y$, the pullback $f^*\mathcal {E}$ is nef if $\mathcal {E}$ is nef, and the converse holds if $f$ is surjective. A vector bundle $\mathcal {E}$ is called numerically flat if $\mathcal {E}$ and its dual $\mathcal {E}^{\vee }$ are both nef.

Note that, by [Bar71, Proposition 3.5], the tensor product of two nef vector bundles are nef again. In particular, if $\mathcal {E}$ is nef, then the exterior products of $\mathcal {E}$ are also nef.

By the same argument as in the case of characteristic zero (cf. [Laz04, Theorem 6.2.12] and [CP91, Proposition 1.2]), we have the following.

Proposition 2.1 (Nef vector bundles)

Let $\mathcal {E}$ be a vector bundle on a smooth projective variety $X$. We have the following:

1. (1) A vector bundle $\mathcal {E}$ is numerically flat if and only if both $\mathcal {E}$ and $\det \mathcal {E}^{\vee }$ are nef.

2. (2) Let $0 \to \mathcal {F} \to \mathcal {E} \to \mathcal {G} \to 0$ be an exact sequence of vector bundles. Assume that $\mathcal {F}$ and $\mathcal {G}$ are nef. Then $\mathcal {E}$ is also nef. Conversely, if $\mathcal {E}$ is nef and $c_1(\mathcal {G}) \equiv 0$, then $\mathcal {F}$ is nef.

3. (3) Assume $\mathcal {E}$ is nef. If $\mathcal {L} \to \mathcal {E}^\vee$ is a non-trivial morphism from a numerically trivial line bundle, then $\mathcal {L}$ defines a subbundle of $\mathcal {E}^\vee$.

Lemma 2.2 (Numerically flat quotient bundles)

Let $\mathcal {E}$ be a nef vector bundle on a smooth projective variety, and $\mathcal {Q}$ a torsion free quotient of $\mathcal {E}$ such that $c_1(\mathcal {Q}) \equiv 0$. Then $\mathcal {Q}$ is a numerically flat vector bundle. Moreover, the kernel of $\mathcal {E} \to \mathcal {Q}$ is a nef vector bundle.

Proof. Consider the dual map $\mathcal {Q}^{\vee } \to \mathcal {E}^{\vee }$. Then the map $\det (\mathcal {Q}^{\vee }) \to \bigwedge ^{\operatorname {rank} \mathcal {Q}} \mathcal {E}^\vee$ is a bundle injection by Proposition 2.1(3). Then, by [DPS94, Lemma 1.20], the sheaf $\mathcal {Q}^{\vee }$ is a subbundle of $\mathcal {E}^{\vee }$. Hence, the composite $\mathcal {E} \to \mathcal {Q} \to \mathcal {Q}^{\vee \vee }$ is surjective. In particular, the map $\mathcal {Q} \to \mathcal {Q}^{\vee \vee }$ is also surjective. Since $\mathcal {Q}$ is torsion free, we have $\mathcal {Q} = \mathcal {Q}^{\vee \vee }$. Now it follows from Proposition 2.1(2) that the kernel of $\mathcal {E} \to \mathcal {Q}$ is a nef vector bundle.

Theorem 2.3 [BD13]

Let $X$ be a smooth projective SRC variety and $\mathcal {E}$ a vector bundle on $X$. Assume that, for any rational curve $f\colon \mathbb {P}^1 \to X$, the pullback $f^{\ast }\mathcal {E}$ is trivial. Then $\mathcal {E}$ itself is trivial.

This implies the following.

Corollary 2.4 (see [Gou14])

For a smooth projective SRC variety $X$, the first cohomology $H^1(X, \mathcal {O}_X)$ vanishes.

3. Separable rational connectedness

In this section, we prove Theorem 1.3 and Corollary 1.4.

3.1 Preliminaries: foliations and SRC

Here we collect several results from [She10], which describe the relation between a variety $X$ being SRC and foliations on $X$.

Let $X$ be a normal projective variety of dimension $n$. A rational curve $f \colon \mathbb {P}^1 \to X$ is called free (respectively, very free) if $f(\mathbb {P}^1)$ is contained in the smooth locus of $X$, and $f^*T_X$ is nef (respectively, ample).

Definition 3.1 (RCC, RC, FRC, and SRC; see [Kol96, Chapter IV. Definition 3.2] and [She10, Definition 1.2])

Let $X$ be a normal projective variety over $k$. Then $X$ is called:

1. (1) rationally chain connected (RCC) if there exist a variety $T$ and a scheme $\mathcal {U}$ with morphisms $(T \xleftarrow {p} \mathcal {U} \xrightarrow {q} X)$ such that

   • – $p$-fibers are connected proper curves with only rational components and

   • – the natural map $q^{(2)} \colon \mathcal {U} \times _T \mathcal {U} \to X \times X$ is dominant;

2. (2) rationally connected (RC) if there exist a variety $T$ and a scheme $\mathcal {U}$ with morphisms $(T \xleftarrow {p} \mathcal {U} \xrightarrow {q} X)$ such that

   • – $p$-fibers are irreducible rational curves and

   • – the natural map $q^{(2)} \colon \mathcal {U} \times _T \mathcal {U} \to X \times X$ is dominant;

3. (3) freely rationally connected (FRC) if there exists a variety $T$ with morphisms $(T \xleftarrow {\operatorname {pr}_2} \mathbb {P}^1 \times T \xrightarrow {q} X)$ such that

   • – each $\operatorname {pr}_2$-fiber defines a free rational curve on $X$ and

   • – the natural map $q^{(2)} \colon \mathbb {P}^1 \times \mathbb {P}^1 \times T \to X \times X$ is dominant;

4. (4) separably rationally connected (SRC) if there exists a variety $T$ with morphisms $(T \xleftarrow {\operatorname {pr}_2} \mathbb {P}^1 \times T \xrightarrow {q} X)$ such that

   • – the natural map $q^{(2)} \colon \mathbb {P}^1 \times \mathbb {P}^1 \times T \to X \times X$ is dominant and smooth at the generic point of $\mathbb {P}^1 \times \mathbb {P}^1 \times T$.

Remark 3.2 (1) Any smooth Fano variety is RCC (see, for instance, [Kol96, Chapter V, Theorem 2.13]).

(2) Note that the definition of SRC here is slightly different from the definition in [She10] (the existence of very free rational curves). However, if $X$ is smooth, then that $X$ is SRC is equivalent to the existence of a very free rational curve on $X$ (see, for instance, [Kol96, Chapter IV, Theorem 3.7]). Thus, the two definitions coincide. Note also that, in the situation of this paper, we mainly consider smooth varieties and, thus, we do not need to care about the differences (cf. the smoothness of $X^{[1]}$ in Proposition 3.20).

(3) In general, the following implications hold:

\[ \text{SRC} \implies \text{FRC} \implies \text{RC} \implies \text{RCC}. \]

Assume that $X$ is smooth and $T_X$ is nef. Then $\text {RCC} \implies \text {FRC}$. This follows from the smoothing technique of free rational curves (see, e.g., [Kol96, Chapter II. 7.6]).

Assume that a normal projective variety $X$ contains a free rational curve $f \colon \mathbb {P}^1 \to X$. Since any vector bundle on $\mathbb {P}^1$ is a direct sum of line bundles, we have

\[ f^* T_X \simeq \bigoplus_{i=1}^{r} \mathcal{O}(a_i) \bigoplus \mathcal{O}^{\oplus n-r} \]

with $a_i >0$.

Definition 3.3 (Positive ranks and maximally free rational curves [She10, Definition 2.1])

In the above notation, the ample subsheaf $\bigoplus _{i=1}^{r} \mathcal {O}(a_i)$ defines a subsheaf of $f^*T_X$ that is independent of the choice of decomposition of $f^*T_X$.

1. (1) This subsheaf $\bigoplus _{i=1}^{r} \mathcal {O}(a_i) \subset f^*T_X$ is called the positive part of $f^*T_X$, and denoted by $\operatorname {Pos} (f^*T_X)$.

2. (2) We call $r = \operatorname {rank} \operatorname {Pos} (f^*T_X)$ the positive rank of the free rational curve $f$.

3. (3) The positive rank of $X$ is defined as the maximum of positive ranks of the free rational curves.

4. (4) A free rational curve $f\colon \mathbb {P}^1 \to X$ is called maximally free if its positive rank is the positive rank of $X$.

Proposition 3.4 [She10, Proposition 2.2]

Let $x \in X$ be a closed point. Assume that there exists a maximally free rational curve $f \colon \mathbb {P}^1 \to X$ with $f(\mathbb {P}^1) \ni x$. Then there exists a $k$-subspace $\mathcal {D} (x) \subset T_X\otimes k(x)$ such that:

• – for every maximally free rational curve $f \colon \mathbb {P}^1 \to X$ with $f(0) = x$, we have

  \[ \operatorname{Pos}(f^*T_X)\otimes k(0) = \mathcal{D} (x) \]
  as a subspace of $T_X \otimes k(x)$.

The next proposition ensures that these subspaces $\mathcal {D} (x)$ patch together to define a subsheaf of $T_X$.

Proposition 3.5 [She10, Proposition 2.5]

There exist a nonempty open subset $U \subset X$ and a subbundle $\mathcal {D} \subset T_U$ such that

\[ \mathcal{D}\otimes k(x) = \mathcal{D} (x) \]

holds for all $x \in U$.

In the following we denote also by $\mathcal {D} \subset T_X$ the saturation of $\mathcal {D}$ in $T_X$ (by an abuse of notation).

Theorem 3.6 [She10, Proposition 2.6]

The sheaf $\mathcal {D}$ defines a foliation. Namely, $\mathcal {D}$ satisfies the following conditions:

1. (1) $\mathcal {D}$ is involutive, i.e. it is closed under the Lie bracket $[\mathcal {D} ,\mathcal {D} ] \subset \mathcal {D}$;

2. (2) $\mathcal {D}$ is $p$-closed, i.e. $\mathcal {D} ^p \subset \mathcal {D}$.

For the convenience of readers, we briefly recall basic properties of foliations and their quotients. For an account of the general theory of foliations, we refer the reader to [Eke87, MP97].

Let $X$ be a smooth projective variety over $k$. Denote by $\sigma \colon X^{(1)} \to X$ the base change of the absolute Frobenius $F_{\operatorname {Spec}(k)}$ on $\operatorname {Spec}(k)$ by the structure morphism $X \to \operatorname {Spec}(k)$ (Note that $F_{\operatorname {Spec}(k)}$ is an isomorphism). By the definition, the absolute Frobenius morphism $F_X \colon X \to X$ factors $X^{(1)}$ and we have the relative Frobenius morphism $X \to X^{(1)}$ over $k$. As a scheme, the topological space of $X^{(1)}$ is that of $X$, and the structure sheaf is $\mathcal {O}_X^p$. The morphism $X \to X^{(1)}$ corresponds to the inclusion $\mathcal {O}_X^p \to \mathcal {O}_X$. By the definition of $\sigma \colon X^{(1)} \to X$, there is a natural identification $\sigma ^{*}T_X = T _{X^{(1)}}$.

A foliation $\mathcal {F}$ on $X$ is a saturated subsheaf of $T_X$ which is closed under the Lie bracket and $p$-closed. Since $T_X$ is the sheaf of derivations $\mathcal {O}_X \to \mathcal {O}_X$, local sections of $\mathcal {F}$ define local derivations $\mathcal {O}_X \to \mathcal {O}_X$. We denote by $\operatorname {Ann}(\mathcal {F}) \subset \mathcal {O}_X$ the subsheaf of sections annihilated by $\mathcal {F}$. By the Leibnitz rule, we have $\mathcal {O}_X^p \subset \operatorname {Ann}(\mathcal {F})$. The quotient $X/\mathcal {F}$ is, by definition, a scheme whose topological space is that of $X$ and structure sheaf $\operatorname {Ann}(\mathcal {F})$. From the inclusions $\mathcal {O}_X^p \subset \operatorname {Ann}(\mathcal {F}) \subset \mathcal {O}_X$, we have morphisms

\[ X \xrightarrow{f} X/\mathcal{F} \xrightarrow{g} X^{(1)} \xrightarrow{\sigma} X. \]

such that:

• – $\sigma \circ g \circ f$ is the absolute Frobenius morphism $F_{X}$;

• – $g \circ f$ is the relative Frobenius morphism over $k$.

Note that $f$ and $g$ are morphisms over $\operatorname {Spec}(k)$, but $\sigma$ is not. It is known that $X/\mathcal {F}$ is normal. Moreover, on the open subset where $\mathcal {F}$ is a subbundle of $T_X$, the variety $X/\mathcal {F}$ is smooth.

Conversely, if $Y$ is a normal variety between $X$ and $X^{(1)}$, then there is a foliation $\mathcal {F}$ such that $Y = X/\mathcal {F}$. This defines a one-to-one correspondence between the set of foliations on $X$ and the set of normal varieties between $X$ and $X^{(1)}$.

On the open subset where $\mathcal {F}$ is a subbundle of $T_X$, we have the following exact sequence of vector bundles:

(3.1)\begin{equation} 0 \to \mathcal{F} \to T_X \xrightarrow{df} f^* T_{X/\mathcal{F}} \to F_{X}^* \mathcal{F} \to 0. \end{equation}

Namely the foliation $\mathcal {F}$ is the kernel of the differential map $df \colon T_X \to f^* T_{X/\mathcal {F}}$. Note that the last map $f^*T_{X/\mathcal {F}} \to F_X^* \mathcal {F}$ is induced from the map $f^*dg \colon f^*T_{X/\mathcal {F}} \to f^*g^*T_{X^{(1)}} = f^*g^*\sigma ^*T_{X} =F_X^*T_X$, i.e. $f^*dg$ factors $F_X^*\mathcal {F} \subset F_X^*T_X$.

Assume for a moment that $\mathcal {F}$ is a subbundle of $T_X$ and, hence, $Y := X/\mathcal {F}$ is smooth. By the functoriality, we have the map $f^{(1)} \colon X^{(1)}\to Y^{(1)}$ and, hence, the variety $X^{(1)}$ is between $Y$ and $Y^{(1)}$. Thus, $X^{(1)}$ is the quotient $Y/\mathcal {G}$ by some foliation $\mathcal {G} \subset T_Y$. On the other hand, by considering the pullback by $\sigma \circ g$, we obtain a subbundle $g^* \sigma ^* \mathcal {F} \subset g^* \sigma ^{*}T_X = g^* T _{X^{(1)}}$. For the ease of reference, we include the following.

Lemma 3.7 Let the notation be as above. Then the differential map $dg \colon T_{Y} \to g^* T_{X^{(1)}}$ factors through $g^* \sigma ^* \mathcal {F}$. The foliation $\mathcal {G}$ is the kernel of the map $T_{Y} \to g^*\sigma ^* \mathcal {F}$. Moreover, we have the following exact sequences:

• – $0 \to \mathcal {G} \to T_{Y} \to g^*\sigma ^* \mathcal {F} \to 0$;

• – $0 \to \mathcal {F} \to T_X \to f^* T_{Y} \to F_{X}^* \mathcal {F} \to 0$.

In particular, $f^*\mathcal {G} \simeq T_X/\mathcal {F}$.

Proof. Since $\mathcal {G}$ corresponds to the quotient $g \colon Y \to X^{(1)} =Y/\mathcal {G}$, we have the following exact sequence:

\[ 0 \to \mathcal{G} \to T_Y \xrightarrow{dg} g^* T_{X^{(1)}} \xrightarrow{\alpha} F_{Y}^* \mathcal{G} \to 0. \]

By pulling back (3.1) by $\sigma \circ g$, we also have the following exact sequence:

\[ 0 \to g^*\sigma^*\mathcal{F} \xrightarrow{\beta} g^*T_{X^{(1)}} \xrightarrow{g^*df^{(1)}} g^*(f^{(1)})^*T_{Y^{(1)}} \to g^*\sigma^*F_{X}^* \mathcal{F} \to 0. \]

Since the composite $g^*df^{(1)} \circ dg = d(f^{(1)} \circ g)$ is a zero map, the differential $dg \colon T_{Y} \to g^* T_{X^{(1)}}$ factors through $g^* \sigma ^* \mathcal {F}$ and, hence, $\mathcal {G}$ is the kernel of the map $T_{Y} \to g^*\sigma ^* \mathcal {F}$.

On the other hand, since the natural map $\mathcal {F} \to f^*T_Y$ is a zero map, so is the composite $g^*\sigma ^*\mathcal {F} \xrightarrow {\beta } g^*T_{X^{(1)}} \xrightarrow {\alpha } F_Y^*\mathcal {G} \hookrightarrow F_Y^*T_Y =g^*\sigma ^*f^*T_Y$. Thus $g^*\sigma ^*\mathcal {F} \xrightarrow {\beta } g^*T_{X^{(1)}} \xrightarrow {\alpha } F_Y^*\mathcal {G}$ is a zero map and, hence, we have the exact sequence

\[ 0 \to \mathcal{G} \to T_{Y} \to g^*\sigma^* \mathcal{F} \to 0. \]

By considering the pullback by $f$, we have the following exact sequence:

\[ 0 \to f^*\mathcal{G} \to f^*T_{Y} \to F_X^* \mathcal{F} \to 0. \]

Combining with (3.1), we have $f^*\mathcal {G} \simeq T_X/\mathcal {F}$.

Now we return to our situation. There exist the quotient $X^{[1]} := X/\mathcal {D}$ and a sequence of morphisms

\[ X \xrightarrow{f} X^{[1]} \xrightarrow{g} X^{(1)} \xrightarrow{\sigma} X. \]

In general, $X^{[1]}$ is normal. In the situation of this paper, however, $\mathcal {D}$ is always a subbundle and, hence, $X^{[1]}$ is smooth (see Proposition 3.20). The following is Shen's theorem.

Theorem 3.8 [She10, Proposition 3.4 and Theorem 5.1]

The following hold:

1. (1) $X$ contains a very free rational curve if and only if $X^{[1]} \simeq X^{(1)}$;

2. (2) if $X$ is FRC, then so is $X^{[1]}$;

3. (3) set $X^{[m+1]} := (X^{[m]})^{[1]}$ inductively; if $X$ is FRC, then $X^{[m]}$ contains a very free rational curve for $m \gg 0$.

The following is a direct consequence of Lemma 3.7.

Proposition 3.9 (Foliations and tangent bundles)

Assume that $\mathcal {D}$ is a subbundle of $T_X$. Then the differential $dg \colon T_{X^{[1]}} \to g^* T_{X^{(1)}}$ factors through $g^* \sigma ^* \mathcal {D}$.

Denote by $\mathcal {K}$ the kernel of the map $T_{X^{[1]}} \to g^* \sigma ^* \mathcal {D}$. Then $\mathcal {K}$ is a foliation on $X^{[1]}$ and we have $f^* \mathcal {K} \simeq T_X/\mathcal {D}$. Moreover, we have the following exact sequence:

• – $0 \to \mathcal {K} \to T_{X^{[1]}} \to g^*\sigma ^* \mathcal {D} \to 0$;

• – $0 \to \mathcal {D} \to T_X \to f^* T_{X^{[1]}} \to F_{X}^* \mathcal {D} \to 0$.

3.2 Action of group schemes $\mu _p$ and $\alpha _p$

Here we briefly recall the relation between vector fields and actions of group schemes $\mu _p$ and $\alpha _p$. See, e.g., [DG70, Chapitre II, § 7], [RŠ76, § 1], and [MN91, § 1] for an account.

Definition 3.10 ($\mu _p$ and $\alpha _p$)

The group schemes $\mu _p$ and $\alpha _p$ are defined as follows:

• – $\mu _p := \operatorname {Spec} k[x]/(x^p -1) \subset \mathbb {G}_m = \operatorname {Spec} k[x,x^{-1}]$;

• – $\alpha _p := \operatorname {Spec} k[x]/(x^p) \subset \mathbb {G}_a = \operatorname {Spec} k[x]$.

Here the group scheme structures are induced from $\mathbb {G}_m$ and $\mathbb {G}_a$.

Proposition 3.11 ($p$-closed vector fields)

Let $X$ be a smooth variety and $D \in H^0(T_X)$ be a vector field.

1. (1) There is a one-to-one correspondence between the set of vector fields $D$ with $D^p = D$ and the set of $\mu _p$-actions on $X$.

2. (2) There is a one-to-one correspondence between the set of vector fields $D$ with $D^p = 0$ and the set of $\alpha _p$-actions on $X$.

Remark 3.12 (Quotients by $\mu _p$ and $\alpha _p$)

Let $X$ be a smooth projective variety and $D$ a vector field with $D^p = D$ or $D^p = 0$. Then there exists the action of $G = \mu _p$ or $\alpha _p$ corresponding to $D$. Then, by [Mum70, § 12, Theorem 1], there exists the quotient $X/G$. Note that the map $X \to X/G$ corresponds to the foliation spanned by $D$.

Lemma 3.13 (cf. [RŠ76, § 1 Lemma 1 and Corollary])

Let $V \subset H^0(T_X)$ be an involutive and $p$-closed $k$-subspace. Then there exists a vector field $D \in V$ such that $D^p =D$ or $D^p = 0$.

Definition 3.14 (Fixed points)

Set $G = \mu _p$ or $\alpha _p$ and consider an action of $G$ on a smooth variety $X$. Let $D$ be the corresponding vector field. Then the set of $G$-fixed points is defined as the zero locus of $D$.

Remark 3.15 A vector field $D \in H^0 (T_X)$ determines a morphism $\varphi _D \colon \mathcal {O} \to T_X$. Then the dual of this map $\varphi _D^{\vee } \colon \Omega \to \mathcal {O}_X$ gives a derivation $f_D := \varphi ^{\vee } \circ d$. Since the sheaf $\Omega _X$ is generated by $d\mathcal {O}_X$ as an $\mathcal {O}_X$-module, the following three subschemes are the same:

1. (1) the zero locus of $D$;

2. (2) the closed subscheme whose ideal is $\operatorname {Im} (\varphi _D^{\vee })$;

3. (3) the closed subscheme whose ideal is generated by $\operatorname {Im} (f_D)$.

Lemma 3.16 [RŠ76, § 1 and Lemma 2]

There exists a $\mu _p$-action on $\mathbb {P}^1$. Moreover, for any $\mu _p$-action on $\mathbb {P}^1$, the set of $\mu _p$-fixed points consists of two points.

Similarly, there exists an $\alpha _p$-action on $\mathbb {P}^1$. Moreover, for any $\alpha _p$-action on $\mathbb {P}^1$, the support of the set of $\alpha _p$-fixed points consists of one point.

Remark 3.17 Since there are only two types of vector fields on $\mathbb {P}^1$, there are only two kinds of group actions as above (up to isomorphism).

3.3 Proof of Theorem 1.3

Throughout this subsection, we assume that:

• – $X$ is a smooth projective variety with nef tangent bundle and moreover $X$ is RCC.

Lemma 3.18 The vector space $N_1(X)$ is spanned by maximally free rational curves.

Proof. It is enough to show that, if a divisor $H$ is not numerically trivial, then $H \cdot C \neq 0$ for some maximally free rational curve $C$.

Note that, by [Kol96, Chapter IV, Theorem 3.13], $N_1 (X)$ is generated by rational curves. Assume $H \not \equiv 0$. Then there exists a rational curve $g \colon \mathbb {P}^1 \to D := g(\mathbb {P}^1) \subset X$ such that $H \cdot D \neq 0$. Since the tangent bundle is nef, the curve $D$ is free.

Let $f \colon \mathbb {P}^1 \to C := f(\mathbb {P}^1) \subset X$ be a maximally free rational curve. Since $C$ and $D$ are both free rational curves, deformations of these curves cover open subsets of $X$ and, hence, we may assume that $C \cap D \neq \emptyset$. Then, by [Kol96, Chapter II, Theorem 7.6], there is a smoothing $C'$ of $C \cup D$.

Claim 3.19 We claim that $C'$ is a maximally free rational curve.

Proof of Claim 3.19 Let $f ' \colon \mathbb {P}^1 \to C' \subset X$ be the normalization of $C'$, and $h \colon Z \to C \cup D \subset X$ a map from the tree of two rational curves to $C\cup D$. Then, by the semicontinuity, we have

\[ h^0(f'^*\Omega_X) \leq h^0(h^*\Omega_X). \]

Let $Z_1$ and $Z_2$ be the irreducible components of $Z$, each of which is isomorphic to $\mathbb {P}^1$, and $p \in Z_1 \cap Z_2$ be the intersection point. We may assume $h|_{Z_1} = f$ and $h|_{Z_2} = g$. Then we have the following exact sequence:

\[ 0 \to g^*\Omega_X (-p) \to h^*\Omega_X \to f^* \Omega_X \to 0. \]

Since $T_X$ is nef, we have $H^0 (g^*\Omega _X (-p)) =0$ and, hence, $h^0 (h^*\Omega _X) \leq h^0 (f^*\Omega _X)$. Thus, we have $h^0 (f'^*\Omega _X) \leq h^0 (f^*\Omega _X)$ and have

\[ \operatorname{rank} \operatorname{Pos} (f') = n - h^0 (f'^*\Omega_X) \geq n- h^0 (f^*\Omega_X) =\operatorname{rank} \operatorname{Pos}(f). \]

Since $f \colon \mathbb {P}^1 \to X$ is maximally free, so is $f'$.

Now, we have $H \cdot C' = H\cdot C + H \cdot D \neq 0$, and the assertion follows.

Proposition 3.20 (Purely inseparable modification)

The quotient $X^{[1]}$ is also a smooth, RCC, projective variety with nef tangent bundle. Moreover, if $X$ is not SRC, then the subsheaf $\mathcal {K} \subset T_{X^{[1]}}$ is a numerically flat non-zero subbundle.

Proof. Consider the exact sequence

\[ 0 \to \mathcal{D} \to T_X \to T_X/\mathcal{D} \to 0. \]

By definition, $T_X/\mathcal {D}$ is trivial on the maximally free rational curves. Note that, since $T_X$ is nef, any rational curve $C$ is free and, hence, it admits a deformation $C'$ such that $T_X/\mathcal {D}$ is locally free on $C'$ [Kol96, Chapter II. Proposition 3.7]. In particular, $c_1(T_X/\mathcal {D} )$ is nef on any rational curve (since $T_X$ is nef and locally free quotients of nef vector bundles are again nef). By the previous lemma, we have $c_1(T_X/\mathcal {D} ) \equiv 0$. Then, by Lemma 2.2, $T_X/\mathcal {D}$ is a numerically flat vector bundle. In particular, $X^{[1]}$ is also smooth. Note that $\mathcal {D}$ is nef by Lemma 2.2.

Recall that there are the following exact sequences:

• – $0 \to \mathcal {K} \to T_{X^{[1]}} \to g^*\sigma ^* \mathcal {D} \to 0$;

• – $0 \to \mathcal {D} \to T_X \to f^* T_{X^{[1]}} \to F_{X}^* \mathcal {D} \to 0$;

and that $f^* \mathcal {K} = T_X/\mathcal {D}$. In particular, $\mathcal {K}$ is a numerically flat vector bundle. Note that, if $\mathcal {K}=0$, then $\mathcal {D} = T_X$. In this case, $X^{[1]} \simeq X^{(1)}$ and, thus, $X$ is SRC. This shows that $\mathcal {K}$ is non-zero if $X$ is not SRC.

Since $\mathcal {D}$ is nef, so is $F_{X}^*\mathcal {D}$. Hence, $f^* T_{X^{[1]}}$ is also nef. In particular, $T_{X^{[1]}}$ is nef.

Since $X$ is RCC, so is $X^{[1]}$.

Corollary 3.21 (Purely inseparable modification and vector fields)

Assume that $X$ is not SRC. Then there exists a positive integer $m>0$ such that $X^{[m]}$ is SRC and $T_{X^{[m]}}$ is nef. Moreover, $T_{X^{[m]}}$ contains an involutive, $p$-closed trivial subbundle $\bigoplus \mathcal {O}$.

In particular, there exists a nowhere vanishing vector field $D$ such that $D ^p=D$ or $D^p=0$.

Proof. By Proposition 3.20, $X^{[i]}$ are all smooth, RCC, projective variety with nef tangent bundle. Note that, for smooth projective varieties, being SRC is equivalent to the existence of very free rational curves.

By Theorem 3.8, there exists an integer $m>0$ such that $X^{[m]}$ is SRC. Since $X$ is not SRC, we may choose $m$ such that $X^{[m-1]}$ is not SRC but $X^{[m]}$ is SRC. Applying Proposition 3.20 to $X^{[m-1]}$, we see that $T_{X^{[m]}}$ contains a numerically flat non-zero subbundle $\mathcal {K}$. By Proposition 2.3, $\mathcal {K}$ is trivial. In addition, by Proposition 3.9, $\mathcal {K}$ is $p$-closed and involutive. The last assertion follows from Lemma 3.13.

The above corollary yields a contradiction to the following proposition.

Proposition 3.22 (Fixed points on SRC varieties)

Let $X$ be a smooth SRC variety. Then any vector field $D$ with $D^p =D$ or $D^p=0$ admits a zero point.

Proof. The proof proceeds as Kollár's proof of simple connectedness of SRC varieties (cf. [Deb03, Corollaire 3.6]).

There is an action of $G = \mu _p$ or $\alpha _p$ that corresponds to $D$. Fix an action of $G$ onto $\mathbb {P}^1$. Note that the set of $G$-fixed points on $\mathbb {P}^1$ is not empty.

Consider the action of $G$ on $X \times \mathbb {P}^1$ and the quotient $(X \times \mathbb {P}^1)/G$. Then we have the following commutative diagram.

Note that, on the open subsets where $G$ acts freely, the above diagram is given by a fiber product and, hence, the general $\pi$-fiber is isomorphic to $X$. Since the general $\pi$-fiber is isomorphic to a SRC variety $X$, $\pi$ admits a section $t \colon \mathbb {P}^1 \to (X\times \mathbb {P}^1)/G$ [GHS03, dJS03].

Then the pullback of this section by $\psi$ gives a $G$-equivariant section $s \colon \mathbb {P}^1 \to X \times \mathbb {P}^1$ of $\operatorname {pr}_2$. Hence, $\operatorname {pr}_1 \circ s$ is also $G$-equivariant. Therefore, we have a $G$-equivariant morphism $\mathbb {P}^1 \to X$. Since any $G$-action on $\mathbb {P}^1$ admits a $G$-fixed point, there exists a $G$-fixed point on $X$.

Proof of Theorem 1.3 The assertion follows from Corollary 3.21 and Proposition 3.22.

Proof of Corollary 1.4 The first assertion follows from a theorem of Kollár [Deb03, Corollaire 3.6] or [She10, Corollary 5.3]. The second assertion follows from Corollary 2.4. The last assertion follows from Theorem 2.3.

4. Existence and smoothness of extremal contractions

In this section, we will prove Theorem 1.5. Throughout this section:

• – $X$ is a smooth projective variety over $k$, and the tangent bundle $T_X$ is nef.

We divide the proof into several steps.

Lemma 4.1 Let $M \to N$ be a finite étale Galois morphism between smooth projective varieties over $k$ and $G$ its Galois group. Assume that $M$ admits a $G$-equivariant contraction $f \colon M \to S$. Then there exist a normal projective variety $T$, a finite morphism $S \to T$ and a contraction $g \colon N \to T$ such that the following diagram commutes.

In particular, if $f$ is smooth, then any fiber of $g$ is irreducible and is the image of an $f$-fiber.

Proof. Consider the quotient map $S \to S/G$. Then there exists a morphism $N \to S/G$ since $N = M/G$. Let $N \to T \to S/G$ be the Stein factorization of the map $N \to S/G$. Then, by the rigidity lemma [Deb01, Lemma 1.15], there exists a morphism $S \to T$ as desired.

In the following we consider a diagram of the following form:

(4.1)

where $p$ is a smooth $\mathbb {P}^1$-fibration, $\mathcal {U}$ and $\mathcal {M}$ are projective varieties, and any $p$-fiber is not contracted to a point by $q$. Two closed points $x$, $y \in X$ are said to be $\mathcal {M}$-equivalent if there exists a connected chain of rational curves parametrized by $\mathcal {M}$ which contains both $x$ and $y$. Given a set $\{ (\mathcal {M}_i \xleftarrow {p_i} \mathcal {U}_i \xrightarrow {q_i} X)\}_{i=1,\ldots,m}$ of diagrams as above, we similarly define the $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence relation as follows: two closed points $x$, $y \in X$ are said to be $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalent if there exists a connected chain of rational curves parametrized by $\mathcal {M}_1 \cup \cdots \cup \mathcal {M}_m$ which contains both $x$ and $y$.

Recall that a family of rational curves is called unsplit if the family $\mathcal {M}$ is projective. For the ease of reference, we include some properties of unsplit family of rational curves on varieties with nef tangent bundles.

Lemma 4.2 [Kol96, Chapter II, Theorem 1.7, Proposition 2.14.1, Theorem 2.15, and Corollary 3.5.3]

An unsplit family of rational curves gives a diagram as (4.1). In this case, $q$ is a smooth morphism. Moreover, $\mathcal {U}$ and $\mathcal {M}$ are smooth projective varieties.

Proposition 4.3 (Existence of contractions)

Let $C$ be a curve parametrized by $\mathcal {M}$ and set $R := \mathbb {R}_{\geq 0} [C] \subset \overline {\operatorname {NE}}(X)$. If $q$ is equidimensional with irreducible fibers, then $R$ is an extremal ray and there exists a contraction of $R$.

Moreover, the contraction is equidimensional with irreducible fibers, each fiber $F$ of the contraction (with its reduced structure) is an $\mathcal {M}$-equivalent class, and $\rho (F) = 1$.

Proof. By [Kan22, Theorem 2.2], we obtain a projective morphism $f \colon X \to Y$ onto a projective normal variety $Y$ such that each fiber is an $\mathcal {M}$-equivalent class; moreover, $f$ is equidimensional with irreducible fibers. Note that the proof of [Kan22, Theorem 2.2] works also in positive characteristic. Let $F$ be a fiber of $f$. Then, by [Kol96, Chapter IV, Proposition 3.13.3], the group of rational equivalence classes of algebraic $1$-cycles with rational coefficients $A_1(F)_{\mathbb {Q}}$ is generated by curves in $\mathcal {M}$. Let $\mathcal {M}_F := p(q^{-1}(F))$ be the closed subset parametrizing $1$-cycles contained in $F$. Then the facts that $F$ is an $\mathcal {M}$-equivalent class and that $q$-fibers are connected imply that $\mathcal {M}_F$ is connected. Thus, $N_1(F) \simeq \mathbb {R}$. In particular, $R$ is an extremal ray and $f$ is the contraction of $R$.

The following is an adaption of [Kol96, Chapter I. Theorem 6.5] in a form that we need along the proof.

Theorem 4.4 [Kol96, Chapter I. Theorem 6.5]

Let $M$, $N$ be two varieties over $k$, and let $h \colon M \to N$ be a proper morphism. Assume that:

• – $N$ is normal;

• – $h$ is equidimensional with irreducible fibers.

Then $M \to N$ is a well-defined family of algebraic cycles in the sense of [Kol96, Chapter I].

Fix a point $m \in M$ and let $F := h^{-1}(h(m))$ be the scheme-theoretic fiber. Assume further that:

1. (1) $F$ is generically reduced;

2. (2) the reduced scheme $F_{\mathrm {red}}$ associated to $F$ is smooth at $m$.

Then $h$ is smooth at $m \in M$.

Proof. The assertion that $M \to N$ is a well-defined family of algebraic cycles follows from [Kol96, Chapter I, Theorem 3.17]. If condition (1) holds, then the cycle-theoretic fiber $h^{[-1]}(h(m))$ is the cycle $F_\mathrm {red}$. Then condition (2) and [Kol96, Chapter I, Theorem 6.5] imply that $h$ is smooth at $m$.

Proposition 4.5 (Smoothness of contractions)

Let $C$ be a curve parametrized by $\mathcal {M}$ and set $R := \mathbb {R}_{\geq 0} [C] \subset \overline {\operatorname {NE}}(X)$.

Assume that $R$ is extremal and the contraction $f \colon X \to Y$ of $R$ exists. Assume, moreover, that:

• – $q$ is smooth;

• – $f$ is equidimensional with irreducible fibers;

• – every $f$-fiber is an $\mathcal {M}$-equivalent class.

Then the following hold:

1. (1) $f$ is smooth;

2. (2) every fiber $F$ of $f$ is an SRC Fano variety with nef tangent bundle;

3. (3) $T_Y$ is again nef.

Proof. Let $F$ be a scheme-theoretic fiber of $f$ and $F_\mathrm {red}$ the reduced scheme associated to $F$.

Step 1 In this step, we show that $F_\mathrm {red}$ is a smooth SRC Fano variety with nef tangent bundle and that the Hilbert scheme of $X$ is smooth of dimension $\dim Y$ at $F_\mathrm {red}$.

Note that $F_{\mathrm {red}}$ is an $\mathcal {M}$-equivalent class. By the same argument as in [SW04, Lemma 4.12], one can show that $F_{\mathrm {red}}$ is smooth, and the normal bundle $N_{F_{\mathrm {red}}/X}$ is numerically flat. Consider the standard exact sequence

\[ 0 \to T_{F_{\mathrm{red}}}\to T_X|_{F_{\mathrm{red}}}\to N_{F_{\mathrm{red}}/X}\to 0. \]

Combining this sequence with Proposition 2.1(2), we see that the tangent bundle $T_{F_{\mathrm {red}}}$ is nef. In addition, by adjunction, $-K_{F_{\mathrm {red}}} \equiv -K_X|_{F_{\mathrm {red}}}$. Thus, $F_{\mathrm {red}}$ is a smooth Fano variety with nef tangent bundle. Then Theorem 1.3 implies that $F_{\mathrm {red}}$ is SRC. Applying Theorem 2.3 and Corollary 2.4, we see that $N_{F_{\mathrm {red}}/X}$ is trivial and $H^1(F_{\mathrm {red}},\mathcal {O}_{F_{\mathrm {red}}})=0$. In particular, the Hilbert scheme is smooth of dimension $\dim Y$ at $[F_{\mathrm {red}}]$.

Step 2 Here we reduce to prove that some fiber of $f$ is generically reduced. Assume for a moment that some fiber of $f$ is generically reduced. Then, since $F_{\mathrm {red}}$ is unobstructed, it is numerically equivalent to a general fiber which is generically reduced by the assumption. This is possible if and only if $F$ is generically reduced. By Theorem 4.4, $f$ is smooth. Finally, $T_Y$ is nef by Proposition 2.1. Thus it is enough to prove that some fiber of $f$ is generically reduced.

Step 3 Let $X_2 = X$ be a copy of $X$ and denote by $X_1$ the original variety $X$. Let $V \subset X \times X$ be the graph of the $\mathcal {M}$-equivalence relation (with its reduced scheme structure). We will denote by $p_1 \colon V \to X_1$ and $p_2 \colon V \to X_2$ the natural projections. In this step, we show that the geometric generic fiber of $p_2 \colon V \to X_2$ is reduced. We follow the proof of [Sta06, Lemma 2.3].

By taking products with $X_2$, we have the following diagram.

Set $V_0 := \Delta \subset X_1 \times X_2$ (the diagonal) and $V_{i+1} := Q(P^{-1}(P(Q^{-1}(V_{i}))))$ inductively. Then, for $m \gg 0$, $V_m = V_{m+1} = \cdots =: V$ is the graph of the $\mathcal {M}$-equivalence relation (with its reduced scheme structure). Denote by $V(x)$ the $\mathcal {M}$-equivalence class of $x \in X$, which is the fiber of $V/X_2$ over the point $x$. Note that $P$ and $Q$ are smooth.

Let $\eta$ be the generic point of $X_2$ and $K$ the algebraic closure of $k(\eta )$. For a scheme $S$ over $X_2$ or a morphism $f$ of $X_2$-schemes, we will denote by $S_K$ or $f_K$ the base change of $S$ by the natural morphism $\operatorname {Spec} K \to X_2$. Note that this morphism $\operatorname {Spec} K \to X_2$ is flat and that taking scheme theoretic image commutes with flat base changes.

By induction, we will prove $(V_i)_K$ are reduced; $(V_0)_K$ is reduced since is isomorphic to $\operatorname {Spec} K$. Assume that $(V_i)_K$ is reduced. Since $Q$ is a smooth morphism, $(Q^{-1}(V_i))_K$ is also reduced. Since taking scheme theoretic image commutes with flat base changes, $(P(Q^{-1}(V_i)))_K$ is isomorphic to $P_K((Q^{-1}(V_i))_K)$, which is reduced. Similarly $(P^{-1}(P(Q^{-1}(V_i))))_K$ and $(Q(P^{-1}(P(Q^{-1}(V_i)))))_K$ are reduced. Thus, $(V_{i+1})_K$ is reduced.

Step 4 Set $V^0 := \{(x,y) \in V \mid \text{$p_2^{-1}(y)$ is reduced} \}$. In this step, we show that:

• – $X_i^0:= p_i(V^0)$ is open in $X_i$ and $p_i^{-1}(X_i^0) = V^0$; moreover, $V^0 \to X_i^0$ is smooth;

• – $Y^0 := f(X_i^0)$ is independent of $i=1$, $2$; moreover, $Y^0$ is open in $Y$ and $X_i^0 = f^{-1}(Y^0)$.

By Theorem 4.4, $p_2$ is smooth at $(x,y) \in V$ if and only if $p_2^{-1}(y)$ is generically reduced. In particular, $p_2^{-1}(y)$ is generically reduced if and only if $p_2^{-1}(y)$ is reduced.

Note that $V$ is the graph of an equivalence relation. From this symmetry, it follows that $p_2^{-1}(y) = p_1^{-1}(x)$ for $(x,y) \in V$. In particular, $p_2^{-1}(y)$ is reduced if and only if $p_1^{-1}(x)$ is reduced. Thus, we have

\[ V^0 =\{(x,y) \in V \mid p_2^{-1}(y)\text{ is reduced} \} = \{(x,y) \in V \mid p_1^{-1}(x)\text{ is reduced} \}. \]

Then $X_i^0 = p_i(V^0)$ is open in $X_i$ and $p_i^{-1}(X_i^0) = V^0$. Note that the subset $Y^0 := f(X_i^0)$ is independent of $i=1$, $2$ because of the symmetry. Moreover, $Y^0$ is open in $Y$ and $X_i^0 = f^{-1}(Y^0)$ since $X_i \setminus X_i^0$ is a closed subset, which is a union of $\mathcal {M}$-equivalent classes.

Step 5 Now we prove some fiber of $X^0_2 \to Y^0$ is generically reduced.

Since $V^0/X_2^0$ is a smooth projective family of subschemes in $X_1$, we have a morphism $X_2^0 \to \operatorname {Hilb}(X_1)$. Then this map factors $Y^0$ by the rigidity lemma [Deb01, Lemma 1.15].

Consider the composite $\gamma \colon p_2^* T_{X_2^0}|_{V^0} \to T_{X _1^0 \times X_2^0}|_{V^0} \to N_{V^0/X_1^0 \times X_2^0}$ of natural homomorphisms. Then the restriction of $\gamma$ to $p_1^{-1}(x_1)$ gives the surjection

\[ T_{X_2^0}|_{p_1^{-1}(x_1)} \to N_{p_1^{-1}(x_1)/X_2^0}. \]

Thus, $\gamma$ is surjective. On the other hand, if we restrict $\gamma$ to $p_2^{-1}(x_2)$, we have a surjection

\[ T_{X_2^0}|_{p_2^{-1}(x_2)} \to N_{p_2^{-1}(x_2)/X_1^0} \]

between trivial vector bundles. Hence, by taking global sections, we have a surjection

\[ T_{X_2^0} \otimes k(x_2) \simeq H^0(T_{X_2^0}|_{p_2^{-1}(x_2)}) \to H^0(N_{p_2^{-1}(x_2)/X_1^0}) \simeq T_{\operatorname{Hilb}(X_1)}\otimes k([p_2^{-1}(x_2)]) \]

of vector spaces and, hence, the map $X_2^0 \to \operatorname {Hilb}(X_1)$ is a smooth morphism. Recall that we have the factorization $X_2^0 \to Y^0 \to \operatorname {Hilb}(X_1)$ with a quasi-finite morphism $Y^0 \to \operatorname {Hilb}(X_1)$. Let $U \subset Y^0$ be a non-empty open subset such that $f^{-1}(U) \to U$ is flat. Then the morphism $U \to \operatorname {Hilb}(X_1)$ is étale. This implies that $f^{-1} (U)\to U$ is smooth. In particular, some fiber of $X^0_2 \to Y^0$ is generically reduced. This completes the proof.

Proposition 4.6 Let $\mathcal {M}$ be a family as in the diagram (4.1) and $[C] \in \mathcal {M}$ be a curve parametrized by $\mathcal {M}$. Assume that $q$ is smooth.

Then $R := \mathbb {R}_{\geq 0} [C]$ is an extremal ray of $X$ and there exists a contraction $f \colon X \to Y$ of $R$ satisfying:

1. (1) $f$ is smooth;

2. (2) any fiber $F$ of $f$ is an SRC Fano variety with nef tangent bundle;

3. (3) $T_Y$ is again nef.

Proof. Let $\mathcal {U} \xrightarrow {q'} X' \xrightarrow {\alpha } X$ be the Stein factorization of $q$. Since $q$ is smooth, so is $\alpha$ (see, for instance, [Gro63, 7.8.10 (i)]). Then we see that $q'$ is also smooth (with irreducible fibers).

First we reduce to the case that the covering $\alpha$ is Galois. There exists a finite étale Galois cover $X'' \to X'$ such that the composite $X'' \to X' \to X$ is also a finite Galois étale cover (see, e.g., [Sza09, Proposition 5.3.9]). Set $\mathcal {U}'' := \mathcal {U} \times _{X'} X''$ and $\mathcal {U}'' \to \mathcal {M}'' \to \mathcal {M}$ be the Stein factorization of $\mathcal {U}'' \to \mathcal {M}$. Then the morphism $\mathcal {U}'' \to \mathcal {M}''$ is a smooth $\mathbb {P}^1$-fibration and we have the following diagram.

Note that this diagram defines the same ray $R$ and the $\mathcal {M}''$-equivalent relation is the $\mathcal {M}$-equivalent relation. Moreover the Stein factorization of $q''$ gives the Galois covering $X'' \to X$.

Therefore, we may assume that the map $\alpha$ is a finite Galois étale cover with Galois group $G := \{g_1, \ldots, g_m\}$. By composing $g_i$ with $q'$, we have the following diagrams.

By Proposition 4.3, there exist the contractions of extremal rays $R_i := (g_i)_*R$.

Let $f_1 \colon X' \to Y_1$ be the contraction of $R_1$. Then $f_1$ is a smooth morphism by Proposition 4.5. Thus, the following diagram

satisfies the assumption of Propositions 4.3 and 4.5 if $p_i$-fibers are not contracted to a point in $Y_1$.

If all rays $R_i$ are contracted by $g \colon X' \to Y_1$, then we have a smooth contraction $g \colon X' \to Y_1$ whose fibers are $\mathcal {M}_1$-equivalent classes, and $g$ contracts all rays $R_i$. Otherwise, for some $i$, the ray $R_i$ is not contracted by $X \to Y_1$ and, hence, $p_i$-fibers are not contracted to a point in $Y_1$. Then, by applying the same argument above, we have a smooth contraction $Y_1 \to Y_2$ whose fibers are $\mathcal {M}_i$-equivalent classes.

Thus, by repeating this procedure, we have a sequence of morphism $X' \to Y_1 \to \cdots \to Y_l$ such that each morphism is a smooth contraction whose fibers are $\mathcal {M}_j$-equivalent classes for some $j$ and that all rays $R_i$ are contracted by $g \colon X' \to Y_l$.

Since each fiber of $g$ is chain connected by curves in the families $\mathcal {M}_i$, each fiber of $g$ is an $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence class. Since the set of diagrams $\{ (\mathcal {M}_i \xleftarrow {p_i} \mathcal {U}_i \xrightarrow {q_i} X)\}_{i=1,\ldots,m}$ is $G$-invariant, the $g_i$-image ($g_i \in G$) of an $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence class is again an $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence class. This implies that there exists a $G$-action on $Y_l$ such that $g$ is $G$-equivariant. By Lemma 4.1, there exists a contraction $f \colon X \to Y$ such that the following diagram commutes.

Since $g$ is smooth, any fiber of $f$ is irreducible and the image of a $g$-fiber (Lemma 4.1). Thus, each $f$-fiber is an $\mathcal {M}$-equivalent class and $f$ is equidimensional with irreducible fibers. Hence, $f$ satisfies the assumption of Proposition 4.5 and the assertions follow.

Remark 4.7 Assume $X$ is RCC, then $X$ is algebraically simply connected. Thus, the map $\mathcal {U} \to X$ has connected fibers. In this case, by Proposition 4.3, we have $\rho (F) = 1$ for any fiber $F$ of the extremal contraction

Proof of Theorem 1.5 Take a rational curve $C$ on $X$ such that $R=\mathbb {R}_{\geq 0}[C]$ and the anti-canonical degree of $C$ is minimal among rational curves in the ray $R$. Let $\mathcal {M}$ be the unsplit family of rational curves containing $[C]$:

Then $q$ is smooth and the assertion follows from Proposition 4.6.

5. Rational chain connectedness and positivity of $-K_X$

In this section, we prove Theorem 1.6. The proof proceeds as [Wat21, Proof of Theorem 4.16]. Here we divide the proof into several steps.

Throughout this section:

• – $X$ denotes a smooth projective variety with nef tangent bundle and $f \colon X \to Y$ is a smooth contraction with RCC fibers.

Note that by Theorem 1.3 all fibers are SRC.

Lemma 5.1 (Correspondence of extremal rays)

Suppose that $R_Y$ is an extremal ray of $\,Y$. Then there exists an extremal ray $R_X$ of $X$ such that $f_*R _X =R_Y$.

On the other hand, if $R_X$ is an extremal ray of $X$, then $f_* R_X$ is an extremal ray unless $f_* R_X = 0$.

Proof. Let $C_Y$ be a rational curve such that the class belongs to $R_Y$ and $-K_Y \cdot C_Y$ is minimum. Since any fiber of $f$ is RCC, it is SRC by Theorem 1.3. Thus, by [GHS03, dJS03], there exists a rational curve $C_X$ on $X$ such that $f|_{C_X} \colon C_X \to C_Y$ is birational. Take such a rational curve $C_X$ with minimum anti-canonical degree $-K_X \cdot C_X$ (note that, since $T_X$ is nef, the $(-K_X)$-degree of any rational curve is at least $2$).

Then, by the minimality of $-K_X$-degree, the family of rational curves of $C_X$ is unsplit. Thus, by Proposition 4.6, $\mathbb {R}_{\geq 0} [C_X]$ defines an extremal ray of $X$.

Conversely, assume that $R_X$ is an extremal ray of $X$. Let $\mathcal {M}$ be a family of minimal rational curves in $R_X$ and let

be the diagram of this family of rational curves. Then $f \circ q$ gives a diagram satisfying the assumption of Proposition 4.6 and, hence, $f_*R_X$ is an extremal ray.

Proposition 5.2 (Relative Picard numbers)

Let $Y \to Z$ be another contraction. Then $\rho (X/Y) =\rho (X/Z) - \rho (Y/Z)$ and we have the following exact sequence:

\[ 0 \to N_1(X/Y) \to N_1(X/Z) \to N_1(Y/Z) \to 0. \]

Proof. Note that any $f$-fiber $F$ is SRC and, in particular, any numerically trivial line bundle on $F$ is trivial (Corollary 2.4).

Thus, the sequence

\[ 0 \to N^1(Y/Z) \to N^1(X/Z) \to N^1(X/Y) \to 0 \]

is exact and the assertions follow.

Theorem 5.3 (Relative Kleiman–Mori cone)

Fix an integer $m$, then the following are equivalent:

1. (1) $\rho (X/Y) =m$;

2. (2) there exists a sequence of smooth contractions of $K$-negative extremal rays

   \[ X=X_0 \to X_1 \to X_2 \to \cdots \to X_{m-1} \to X_{m} = Y; \]

3. (3) $\operatorname {NE} (X/Y)$ is a closed simplicial cone of dimension $m$, and it is generated by $K_X$-negative extremal rays.

In particular, any fiber $F$ is a smooth Fano variety.

Proof. The proof proceeds by induction on $m$. If $m =1$, then the equivalence of the three conditions follows from Theorem 1.5.

Assume $m \geq 2$. Note that (3) $\implies$ (1) is trivial. Also note that Proposition 5.2 implies (2) $\implies$ (1).

Now, we prove (1) $\implies$ (2). Since $K_X$ is not $f$-nef, there exists a $K_X$-negative extremal ray $R \subset \overline {\operatorname {NE}} (X/Y)$. By Theorem 1.5, there exists a smooth contraction $f_1 \colon X \to X_1$ of $R$, and $f$ factors through $X_1$:

\[ X \xrightarrow{f_1} X_1 \to Y. \]

Since $f_1$ is smooth and any fiber of $f$ is RCC, the morphism $X_1 \to Y$ is also smooth and fibers are RCC. Since $\rho (X_1/Y)< m$, the contraction $X_1 \to Y$ satisfies the three conditions. Hence, condition (2) holds for $f \colon X \to Y$.

Finally, we prove (2) $\implies$ (3). Since $\rho (X/X_{m-1}) < m$ by Proposition 5.2, the contraction $g \colon X \to X_{m-1}$ satisfies the three conditions. In particular, $\operatorname {NE}(X/{X_{m-1}})$ is a simplicial $K_X$-negative face of dimension $m-1$. Denote by $R_1 =\mathbb {R}_{\geq 0} [C_1]$, …, $R_{m-1}=\mathbb {R}_{\geq 0} [C_{m-1}]$ the extremal rays of $\operatorname {NE}(X/{X_{m-1}})$, which are spanned by curves $C_i$. Note also that $X_{m-1} \to Y$ is a contraction of an extremal ray $R_{X_{m-1}}$.

Then, by Lemma 5.1, there exists an extremal ray $R$ of $X$ such that $g_* R = R_{X_{m-1}}$. Let $h \colon X \to Z$ be the contraction of $R$, then we have the following commutative diagram.

Note that, by the inductive hypothesis, each morphism $g$, $h$, $u$, and $v$ satisfies the three conditions. Since $N_1(X/X_{m-1}) \to N_1(Z/Y)$ is a surjective homomorphism between the same dimensional vector spaces, it is an isomorphism.

By Lemma 5.1, the map $N_1(X/X_{m-1}) \to N_1(Z/Y)$ sends each extremal ray to an extremal ray. Thus, $\overline {\operatorname {NE}}(X/X_{m-1}) \simeq \overline {\operatorname {NE}}(Z/Y)$ since these two cones are simplicial. In particular, $\overline {\operatorname {NE}}(Z/Y)$ is spanned by $h_*(C_i)$ ($i=1$, …, $m-1$).

Let $C$ be an irreducible curve on $X$ such that $f(C)$ is a point. Then $h_*(C) \in \operatorname {NE}(Z/Y)$. Thus, we may write

\[ h_*(C) = \sum_{i=1}^{m-1} a_i h_*(C_i) \]

with non-negative real numbers $a_i$. Thus, $C - \sum _{i=1}^{m-1} a_i C_i \in \operatorname {Ker}(h_*) = N_1(X/Z)$. Since $g^*H \cdot (C - \sum _{i=1}^{m-1} a_i C_i) \geq 0$ for any ample divisor $H$ on $X_{m-1}$, we see that

\[ C - \sum_{i=1}^{m-1} a_i C_i \in R. \]

This proves $\overline {\operatorname {NE}}(X/Y)$ is spanned by $R,R_1,\ldots,R_{m-1}$, and hence it is simplicial (since $\rho (X/Y) =m$).

Remark 5.4 If $X$ is RCC or, equivalently, a Fano variety, then each $X_i$ is also a Fano variety. Thus, by Remark 4.7, the fibers of $X_i \to X_{i+1}$ have Picard number one. Then, by arguing as above, we can show that each fiber $F$ of the contraction $X \to Y$ is a Fano variety with $\rho (F) = m$. Moreover, $N_1(F)$ and $\operatorname {NE}(F)$ are identified with $N_1(X/Y)$ and $\operatorname {NE}(X/Y)$, respectively, via the inclusion.

6. Decomposition of varieties with nef tangent bundles

Proof of Theorem 1.8 Here we will prove Theorem 1.8. If $K_X$ is nef, then $T_X$ is numerically flat and $\varphi =\operatorname {id} \colon X \to X$ gives the desired contraction.

Assume that $K_X$ is not nef. By Mori's cone theorem, we can find an extremal ray $R \subset \overline {\operatorname {NE}}(X)$ of $X$. Then, by Theorem 1.5, there exists a smooth contraction $f \colon X \to Y$ of $R$ and the tangent bundle of $Y$ is again nef. By induction on the dimension, $Y$ admits a smooth contraction $\varphi ' \colon Y \to M$ satisfying the conditions in Theorem 1.8. Set $\varphi := \varphi ' \circ f$.

Let $F$ be a fiber of $\varphi$. Then $T_F$ is nef. Moreover, since any fiber of $f$ is SRC and any fiber of $\varphi '$ is RCC, it follows that $F$ is RCC [GHS03, dJS03]. Hence, $F$ is a smooth Fano variety by Theorem 1.6.

Corollary 6.1 (Contraction of extremal faces)

Let $X$ be a smooth projective variety with nef tangent bundle and $\varphi \colon X \to M$ be the decomposition morphism as in Theorem 1.8. Then $\operatorname {NE}(X/M)$ is simplicial. Any set of $K_X$-negative extremal rays spans an extremal face.

Moreover, for any $K_X$-negative extremal face $F$, there exists the contraction of $F$ and it is a smooth morphism satisfies the three equivalent conditions in Theorem 5.3.

7. $F$-liftable varieties with nef tangent bundles

Here we apply our results to prove Theorem 1.12

7.1 Preliminaries on $F$-liftability

Definition 7.1 ($F$-liftable varieties)

Let $X$ be a projective variety over $k$.

1. (1) A lifting of $X$ (modulo $p^2$) is a flat scheme $\widetilde {X}$ over the ring $W_2(k)$ of Witt vectors of length two with $\widetilde {X}\times _{{\operatorname {Spec}} W_2(k)} \operatorname {Spec} (k) \cong X$.

2. (2) For such a lifting $\widetilde {X}$ of $X$, a lifting of Frobenius on $X$ to $\widetilde {X}$ is a morphism $\widetilde {F_X} \colon \widetilde {X} \to \widetilde {X}$ such that the restriction $\widetilde {F_X}|_X$ coincides with the Frobenius morphism $F_X$; then the pair $(\widetilde {X}, \widetilde {F_X})$ is called a Frobenius lifting of $X$. If there exists such a pair, $X$ is said to be F-liftable.

Proposition 7.2 ($F$-liftable varieties)

For a smooth $F$-liftable projective variety $X$, the following hold.

1. (1) For any finite étale cover $Y \to X$, $Y$ is also F-liftable.

2. (2) Let $f \colon X \to Y$ be a contraction and assume $R^1f_{\ast }\mathcal {O}_X=0$. Then $Y$ and any fiber $F$ of $f$ are also F-liftable.

Proof. Part (1) follows from [AWZ21, Lemma 3.3.5]. Part (2) follows from [AWZ21, Theorem 3.3.6 (b)] and [AWZ23, Corollary 5.3 (b)].

7.2 Proof of Theorem 1.12

Definition 7.3 ($F$-liftable and nef tangent bundle)

Let $X$ be a smooth projective variety. For convenience, let us introduce the following condition:

1. (FLNT) $X$ is $F$-liftable and the tangent bundle is nef.

Proposition 7.4 [AWZ21, Proposition 6.3.2]

Let $X$ be a smooth Fano variety satisfying the condition (FLNT). If $\rho _X=1$, then $X$ is isomorphic to a projective space.

Proposition 7.5 ($F$-liftable varieties with $K_X \equiv 0$)

Let $X$ be a smooth projective $F$-liftable variety. If the canonical divisor $K_X$ is numerically trivial, then there exists a finite étale cover $f\colon Y \to X$ from an ordinary abelian variety $Y$.

Proof. See, for instance, [AWZ21, Theorem 5.1.1].

Proposition 7.6 (FLNT Fano varieties)

Let $X$ be a smooth Fano variety satisfying the condition (FLNT). Then $X$ is isomorphic to a product of projective spaces.

Proof. We proceed by induction on the Picard number $\rho _X$. By Proposition 7.4, our assertion holds for the case $\rho _X=1$. Assume that $\rho _X \geq 2$. Then there exists a two-dimensional extremal face, which is spanned by two extremal rays $R_1$ and $R_2$. We denote the contraction of the extremal ray $R_i$ by $f_i\colon X \to X_i$ ($i=1$, $2$), which is a smooth $\mathbb {P}$-fibration by Theorem 1.5, Remark 4.7, and Proposition 7.4. By the induction hypothesis, each $X_i$ is a product of projective spaces and, hence, the Brauer group of $X_i$ vanishes; this implies that each $f_i$ is given by a projectivization of a vector bundle. When $\rho _X=2$, applying [Sat85, Theorem A] $X$ is isomorphic to a product of two projective spaces or $\mathbb {P}(T_{\mathbb {P}^n})$. However, the latter does not occur, because $\mathbb {P}(T_{\mathbb {P}^n})$ is not F-liftable by [AWZ21, Lemma 6.4.3]. Thus, we may assume that $\rho _X \geq 3$. Let $\pi \colon X \to X_{1,2}$ be the contraction of the extremal face $R_1+R_2$. By the rigidity lemma [Deb01, Lemma 1.15], there is the following commutative diagram.

Let us take a vector bundle $\mathcal {E}$ on $X_1$ such that $X \cong \mathbb {P}(\mathcal {E})$ and $f_1\colon X \to X_1$ is given by the natural projection $\mathbb {P}(\mathcal {E}) \to X_1$. For any point $p \in X_{1,2}$, $\pi ^{-1}(p)$ is a smooth Fano variety of Picard number two satisfying the condition (FLNT); by the induction hypothesis it is a product of two projective spaces. Therefore, for a point $p \in X_{1,2}$, we have $\mathcal {E}|_{g_1^{-1}(p)} \simeq \mathcal {O}(a)^{\oplus \operatorname {rank} \mathcal {E}}$. From the continuity of the first Chern class, the number $a$ is independent from $p \in X_{1,2}$. Thus, by tensoring $\mathcal {E}$ with a line bundle, we may assume that $\mathcal {E}|_{g_1^{-1}(p)}$ is trivial for any point $p \in X_{1,2}$. By Grauert's theorem [Har77, III. Corollary 12.9], we see that ${g_1}_\ast (\mathcal {E})$ is a vector bundle on $X_{1,2}$. Then it is straightforward to verify that the natural map ${g_1}^{\ast }({g_1}_\ast (\mathcal {E})) \to \mathcal {E}$ is an isomorphism via Nakayama's lemma. Thus, we have

\[ X=\mathbb{P}(\mathcal{E})\cong \mathbb{P}({g_1}^{\ast}({g_1}_\ast(\mathcal{E})))\cong X_1\times_{X_{1,2}} \mathbb{P}({g_1}_\ast(\mathcal{E})). \]

Again, by the inductive hypothesis, $X_1\cong \prod _{j=1}^{\rho _X-1} \mathbb {P}^{n_j}$ and $X_{1,2}\cong \prod _{j=2}^{\rho _X-1} \mathbb {P}^{n_j}$; we also see that $X_1 \to X_{1,2}$ is a natural projection. This concludes that $X$ is isomorphic to $\mathbb {P}^{n_1}\times \mathbb {P}({g_1}_\ast (\mathcal {E}))$. Since $\mathbb {P}({g_1}_\ast (\mathcal {E}))$ is a product of projective spaces, our assertion holds.

Corollary 7.7 (Structure theorem of FLNT varieties)

Let $X$ be a smooth projective variety satisfying the condition (FLNT). Then there exists a $K_X$-negative contraction $\varphi \colon X \to M$ which satisfy the following properties:

1. (1) $M$ is an étale quotient of an ordinary abelian variety $A$;.

2. (2) $\varphi$ is a smooth morphism whose fibers are isomorphic to a product of projective spaces.

In particular, there exist a finite étale cover $Y \to X$ and a smooth contraction $f \colon Y \to A$ onto an ordinary abelian variety $A$ such that all $f$-fibers are isomorphic to a product of projective spaces.

Proof. By Theorem 1.8, $X$ admits a smooth fibration $\varphi \colon X \to M$ such that all fibers are smooth Fano varieties and the tangent bundle of $M$ is numerically flat. Since Corollary 1.4 implies that $H^1(F, \mathcal {O}_F) = 0$ for all fiber $F$ of $\varphi$, we have $R^1\varphi _* \mathcal {O}_X =0$. Hence, all fibers $F$ and the image $M$ are $F$-liftable by Proposition 7.2. In particular, $F$ is isomorphic to a product of projective spaces and $M$ is an étale quotient of an ordinary abelian variety $A$.

Set $Y := X \times _M A$ and let $f \colon Y \to A$ be the natural projection. Then the last assertion follows.

Proof of Theorem 1.12 By Corollary 7.7, there exist a finite étale cover $\tau _1\colon Y_1 \to X$ and a smooth $(\prod \mathbb {P}^{n_i})$-fibration $f_1\colon Y_1 \to A_1$ over an ordinary abelian variety. We may find a finite étale cover $\tau _2\colon Y \to Y_1$ such that the composite $Y \to Y_1 \to X$ is an étale Galois cover (see, for instance, [Sza09, Proposition 5.3.9]). We denote the Albanese morphism by $\alpha := \alpha _{Y} \colon Y \to A := \operatorname {Alb}(Y)$. By the universal property of the Albanese variety, we obtain a morphism $\tau _3 \colon A \to A_1$ which satisfies the following commutative diagram.

Here we prove that $\tau _3$ is étale. All $f_1$-fibers are isomorphic to $\prod \mathbb {P}^{n_i}$ and, hence, algebraically simply connected. Thus each $f_1 \circ \tau _2$-fiber is a disjoint union of $\prod \mathbb {P}^{n_i}$. In particular, $f_1 \circ \tau _2$-fibers are contracted by $\alpha$. Therefore, $\tau _3$ is finite. Since $f_1 \circ \tau _2$ is surjective, the morphism $\tau _3$ is also surjective. In particular, $\tau _3$ is a finite surjective morphism between abelian varieties. This, in turn, implies that $\alpha$ is surjective with equidimensional fibers. Thus, $\alpha$ is flat. Since $\tau _3 \circ \alpha$ is smooth, $\tau _3$ is étale.

Since $\tau _3$ is étale and $\tau _3 \circ \alpha$ is smooth, the morphism $\alpha$ is smooth. Thus, it is enough to show that $\alpha$-fibers are connected. To prove this, let us consider the Stein factorization $Y \xrightarrow {q_1} A' \xrightarrow {q_2} A$, where $q_1$ is a contraction and $q_2$ is a finite morphism. Since $q_2$ is étale, $A'$ is an abelian variety (see, for instance, [Mum70, Section 18]). This implies that $q_1\colon Y \to A'$ factors through $\alpha \colon Y \to A$, that is, there exists a morphism $\beta \colon A\to A'$ such that $q_1 =\beta \circ \alpha$. By virtue of the universality of $A$ and the rigidity lemma [Deb01, Lemma 1.15] for $q_1$, we see that $\beta$ is an isomorphism and the assertion follows.