Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Morgenbesser, Johannes F.
2010.
The sum of digits of squares in Z[i].
Journal of Number Theory,
Vol. 130,
Issue. 7,
p.
1433.
Drmota, Michael
and
Mauduit, Christian
2010.
Weyl sums over integers with affine digit restrictions.
Journal of Number Theory,
Vol. 130,
Issue. 11,
p.
2404.
Pollack, Paul
and
Shevelev, Vladimir
2012.
On perfect and near-perfect numbers.
Journal of Number Theory,
Vol. 132,
Issue. 12,
p.
3037.
Morgenbesser, Johannes F.
Steiner, Wolfgang
and
Thuswaldner, Jörg M.
2013.
Patterns in Rational Base Number Systems.
Journal of Fourier Analysis and Applications,
Vol. 19,
Issue. 2,
p.
225.
Bourgain, Jean
2014.
Monotone Boolean functions capture their primes.
Journal d'Analyse Mathématique,
Vol. 124,
Issue. 1,
p.
297.
Azaiez, Najib Ouled
Mkaouar, Mohamed
and
Thuswaldner, Jörg M.
2014.
Sur les chiffres des nombres premiers translatés.
Functiones et Approximatio Commentarii Mathematici,
Vol. 51,
Issue. 2,
Mkaouar, M.
and
Wannes, W.
2014.
On the Number of Restricted Prime Factors of an Integer.
Acta Mathematica Hungarica,
Vol. 143,
Issue. 1,
p.
88.
Pollack, Paul
and
Thompson, Lola
2015.
Arithmetic functions at consecutive shifted primes.
International Journal of Number Theory,
Vol. 11,
Issue. 05,
p.
1477.
ALOUI, KARAM
2015.
On the order of magnitude of some arithmetical functions under digital constraint I.
Proceedings - Mathematical Sciences,
Vol. 125,
Issue. 4,
p.
457.
Dartyge, Cécile
Mauduit, Christian
and
Sárközy, András
2015.
Polynomial values and generators with missing digits in finite fields.
Functiones et Approximatio Commentarii Mathematici,
Vol. 52,
Issue. 1,
Rivat, Joël
and
Sárközy, András
2015.
Analytic Number Theory.
p.
345.
Mkaouar, M.
and
Wannes, W.
2016.
On the normal number of prime factors of φ(n) subject to certain congruence conditions.
Journal of Number Theory,
Vol. 160,
Issue. ,
p.
629.
Gómez-Pérez, Domingo
and
Shparlinski, Igor E.
2018.
Arithmetic Properties of Integers in Chains and Reflections of g-ary Expansions.
Experimental Mathematics,
Vol. 27,
Issue. 2,
p.
184.
Martin, Bruno
Mauduit, Christian
and
Rivat, Joël
2019.
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 18,
Issue. 1,
p.
189.
Swaenepoel, Cathy
2020.
Prime numbers with a positive proportion of preassigned digits.
Proceedings of the London Mathematical Society,
Vol. 121,
Issue. 1,
p.
83.
Drappeau, S.
and
Hanna, G.
2020.
The Thue–Morse and Rudin–Shapiro sequences at primes in principal number fields.
Acta Mathematica Hungarica,
Vol. 162,
Issue. 1,
p.
130.
Liu, H.
and
Mauduit, C.
2021.
On the distribution of the truncated sum-of-digits function of polynomial sequences in residue classes.
Acta Mathematica Hungarica,
Vol. 164,
Issue. 2,
p.
360.
Wannes, Walid
2022.
Large Bias Amongst Products of Two Primes.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 45,
Issue. 2,
p.
623.
Car, Mireille
and
Mauduit, Christian
2022.
Le poids des polynômes irréductibles à coefficients dans un corps fini.
Journal d'Analyse Mathématique,
Vol. 146,
Issue. 2,
p.
441.
Spiegelhofer, Lukas
2023.
Collisions of digit sums in bases 2 and 3.
Israel Journal of Mathematics,
Vol. 258,
Issue. 1,
p.
475.


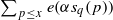 (where the sum is restricted to
(where the sum is restricted to 