Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T01:27:27.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Parity duality for the amplituhedron

Part of: Arithmetic rings and other special rings Polytopes and polyhedra Special varieties

Published online by Cambridge University Press:  09 December 2020

Pavel Galashin  and
Thomas Lam
Pavel Galashin
Affiliation:
Department of Mathematics, University of California, Los Angeles, 520 Portola Plaza, Los Angeles, CA90025, [email protected]
Thomas Lam
Affiliation:
Department of Mathematics, University of Michigan, 2074 East Hall, 530 Church Street, Ann Arbor, MI48109-1043, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

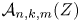The (tree) amplituhedron $\mathcal {A}_{n,k,m}(Z)$ is a certain subset of the Grassmannian introduced by Arkani-Hamed and Trnka in 2013 in order to study scattering amplitudes in 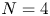$N=4$ supersymmetric Yang–Mills theory. Confirming a conjecture of the first author, we show that when 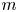$m$ is even, a collection of affine permutations yields a triangulation of 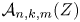$\mathcal {A}_{n,k,m}(Z)$ for any 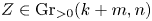$Z\in \operatorname {Gr}_{>0}(k+m,n)$ if and only if the collection of their inverses yields a triangulation of 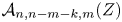$\mathcal {A}_{n,n-m-k,m}(Z)$ for any 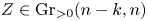$Z\in \operatorname {Gr}_{>0}(n-k,n)$. We prove this duality using the twist map of Marsh and Scott. We also show that this map preserves the canonical differential forms associated with the corresponding positroid cells, and hence obtain a parity duality for amplituhedron differential forms.

Keywords

amplituhedrontwist maptotal positivityGrassmannianpositroid cellsscattering amplitudescyclic polytopes

MSC classification

Primary: 14M15: Grassmannians, Schubert varieties, flag manifolds
Secondary: 13F60: Cluster algebras 52B99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 11 , November 2020 , pp. 2207 - 2262
Check for updates
Copyright
© The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was partially supported by the National Science Foundation under Grants No. DMS-1954121 (P.G.), No. DMS-1464693 (T.L.), and No. DMS-1953852 (T.L.).

References

Arkani-Hamed, N., Bai, Y. and Lam, T., Positive geometries and canonical forms, J. High Energ. Phys. 2017(11) (2017), 39.Google Scholar
Arkani-Hamed, N., Bourjaily, J., Cachazo, F., Goncharov, A., Postnikov, A. and Trnka, J., Grassmannian geometry of scattering amplitudes (Cambridge University Press, Cambridge, 2016).CrossRefGoogle Scholar
Arkani-Hamed, N., Thomas, H. and Trnka, J., Unwinding the amplituhedron in binary, J. High Energy Phys. 2018(1) (2018), 16.CrossRefGoogle Scholar
Arkani-Hamed, N. and Trnka, J., The amplituhedron, J. High Energy Phys. 2014(10) (2014), 30.CrossRefGoogle Scholar
Berenstein, A., Fomin, S. and Zelevinsky, A., Parametrizations of canonical bases and totally positive matrices, Adv. Math. 122 (1996), 49–149.CrossRefGoogle Scholar
Berenstein, A. and Zelevinsky, A., Total positivity in Schubert varieties, Comment. Math. Helv. 72 (1997), 128–166.CrossRefGoogle Scholar
Billera, L. J., Kapranov, M. M. and Sturmfels, B., Cellular strings on polytopes, Proc. Amer. Math. Soc. 122 (1994), 549–555.CrossRefGoogle Scholar
Britto, R., Cachazo, F. and Feng, B., New recursion relations for tree amplitudes of gluons, Nuclear Phys. B 715 (2005), 499–522.CrossRefGoogle Scholar
Britto, R., Cachazo, F., Feng, B. and Witten, E., Direct proof of the tree-level scattering amplitude recursion relation in Yang-Mills theory, Phys. Rev. Lett. 94 (2005), 181602.CrossRefGoogle ScholarPubMed
Brouwer, L. E. J., Beweis der Invarianz des $n$-dimensionalen Gebiets, Math. Ann. 71 (1912), 305–313.CrossRefGoogle Scholar
Edelman, P. H., Rambau, J. and Reiner, V., On subdivision posets of cyclic polytopes, European J. Combin. 21 (2000), 85–101.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. I. Foundations, J. Amer. Math. Soc. 15 (2002), 497–529 .CrossRefGoogle Scholar
Frieden, G., The geometric $R$-matrix for affine crystals of type $A$, Preprint (2017), arXiv:1710.07243.Google Scholar
Galashin, P., Karp, S. N. and Lam, T., The totally nonnegative Grassmannian is a ball, Preprint (2017), arXiv:1707.02010.Google Scholar
Gelfand, I. M., Kapranov, M. M. and Zelevinsky, A. V., Discriminants, resultants and multidimensional determinants. Modern Birkhäuser Classics, 1994 edition reprint (Birkhäuser Boston, Boston, MA, 2008).Google Scholar
Golden, J. K., Goncharov, A. B., Spradlin, M., Vergu, C. and Volovich, A., Motivic amplitudes and cluster coordinates, J. High Energy Phys. 2014(1) (2014), 91.CrossRefGoogle Scholar
Greenberg, M. J. and Harper, J. R., Algebraic topology, Mathematics Lecture Note Series, A First Course, vol. 58 (Benjamin/Cummings Publishing, Reading, MA, 1981).Google Scholar
Karp, S. N., Moment curves and cyclic symmetry for positive Grassmannians. Bull. Lond. Math. Soc. 51 (2019), 900–916.Google Scholar
Karp, S. N. and Williams, L. K., The $m=1$ amplituhedron and cyclic hyperplane arrangements, Int. Math. Res. Not. IMRN 2019 (2017), 1401–1462.CrossRefGoogle Scholar
Karp, S. N., Williams, L. K. and Zhang, Y. X., Decompositions of amplituhedra, Preprint (2017), arXiv:1708.09525.Google Scholar
Knutson, A., Lam, T. and Speyer, D. E., Positroid varieties: juggling and geometry, Compos. Math. 149 (2013), 1710–1752.CrossRefGoogle Scholar
Lam, T., Affine Stanley symmetric functions, Amer. J. Math. 128 (2006), 1553–1586.CrossRefGoogle Scholar
Lam, T., Amplituhedron cells and Stanley symmetric functions, Comm. Math. Phys. 343 (2016), 1025–1037.CrossRefGoogle Scholar
Lam, T., Totally nonnegative Grassmannian and Grassmann polytopes, Current Developments in Mathematics, vol. 2014 (International Press, Somerville, MA, 2016), 51–152.Google Scholar
Leclerc, B. and Zelevinsky, A., Quasicommuting families of quantum Plücker coordinates, in Kirillov's seminar on representation theory, American Mathematical Society Translations: Series 2, vol. 181 (American Mathematical Society, Providence, RI, 1998), 85–108.CrossRefGoogle Scholar
MacMahon, P. A., Combinatory analysis. Vol. I, II (bound in one volume), Dover Phoenix Editions (Dover Publications, Mineola, NY, 2004). Reprint of An introduction to combinatory analysis (1920) and Combinatory analysis. Vol. I, II (1915, 1916).Google Scholar
Marsh, R. J. and Scott, J. S., Twists of Plücker coordinates as dimer partition functions, Comm. Math. Phys. 341 (2016), 821–884.CrossRefGoogle Scholar
Muller, G. and Speyer, D. E., The twist for positroid varieties, Proc. Lond. Math. Soc. (3) 115 (2017), 1014–1071.CrossRefGoogle Scholar
Oh, S., Postnikov, A. and Speyer, D. E., Weak separation and plabic graphs, Proc. Lond. Math. Soc. (3) 110 (2015), 721–754.CrossRefGoogle Scholar
Oppermann, S. and Thomas, H., Higher-dimensional cluster combinatorics and representation theory, J. Eur. Math. Soc. (JEMS) 14 (2012), 1679–1737.CrossRefGoogle Scholar
Postnikov, A., Total positivity, Grassmannians, and networks, Preprint (2007), http://math.mit.edu/~apost/papers/tpgrass.pdf.Google Scholar
Rambau, J., Triangulations of cyclic polytopes and higher Bruhat orders, Mathematika 44 (1997), 162–194.CrossRefGoogle Scholar
Rambau, J. and Santos, F., The generalized Baues problem for cyclic polytopes. I, European J. Combin. 21 (2000), 65–83. Combinatorics of polytopes.CrossRefGoogle Scholar
Reiner, V., The generalized Baues problem, in New perspectives in algebraic combinatorics (Berkeley, CA, 1996–97), Mathematical Sciences Research Institute Publications, vol. 38 (Cambridge University Press, Cambridge, 1999), 293–336.Google Scholar
Scott, R. F., Note on a theorem of Prof. Cayley's, Messeng. Math. 8 (1879), 155–157.Google Scholar
Scott, J. S., Grassmannians and cluster algebras, Proc. London Math. Soc. (3) 92 (2006), 345–380.CrossRefGoogle Scholar
Stanley, R. P., Enumerative combinatorics. Vol. 2, Cambridge Studies in Advanced Mathematics, vol. 62 (Cambridge University Press, Cambridge, 1999). With a foreword by Gian-Carlo Rota and appendix 1 by Sergey Fomin.CrossRefGoogle Scholar
Sturmfels, B., Totally positive matrices and cyclic polytopes, Linear Algebra Appl. 107 (1988), 275–281.Google Scholar
Thomas, H., New combinatorial descriptions of the triangulations of cyclic polytopes and the second higher Stasheff-Tamari posets, Order 19 (2002), 327–342.CrossRefGoogle Scholar