Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T04:34:28.636Z Has data issue: false hasContentIssue false
  • English
  • Français

The 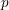$p$-adic Gross–Zagier formula on Shimura curves

Part of: Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  11 July 2017

Daniel Disegni
Daniel Disegni*
Affiliation:
Departement de Mathématiques, Université Paris-Sud, 91405 Orsay Cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a general formula for the 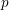$p$-adic heights of Heegner points on modular abelian varieties with potentially ordinary (good or semistable) reduction at the primes above 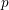$p$. The formula is in terms of the cyclotomic derivative of a Rankin–Selberg 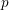$p$-adic 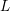$L$-function, which we construct. It generalises previous work of Perrin-Riou, Howard, and the author to the context of the work of Yuan–Zhang–Zhang on the archimedean Gross–Zagier formula and of Waldspurger on toric periods. We further construct analytic functions interpolating Heegner points in the anticyclotomic variables, and obtain a version of our formula for them. It is complemented, when the relevant root number is 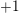$+1$ rather than 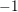$-1$, by an anticyclotomic version of the Waldspurger formula. When combined with work of Fouquet, the anticyclotomic Gross–Zagier formula implies one divisibility in a 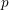$p$-adic Birch and Swinnerton-Dyer conjecture in anticyclotomic families. Other applications described in the text will appear separately.

Keywords

Gross–Zagier formulap-adic L-functionHeegner pointsp-adic heightsBirch and Swinnerton-Dyer conjecture

MSC classification

Primary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Secondary: 11F33: Congruences for modular and $p$-adic modular forms 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 10 , October 2017 , pp. 1987 - 2074
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aflalo, E. and Nekovář, J., Non-triviality of CM points in ring class field towers , Israel J. Math. 175 (2010), 225–284; with an appendix by Christophe Cornut, doi:10.1007/s11856-010-0011-3; MR 2607546 (2011j:11108).Google Scholar
Agboola, A. and Howard, B., Anticyclotomic Iwasawa theory of CM elliptic curves , Ann. Inst. Fourier (Grenoble) 56 (2006), 1001–1048; in English, with English and French summaries;MR 2266884 (2009b:11098).Google Scholar
Amice, Y. and Vélu, J., Distributions p-adiques associées aux séries de Hecke , in Journées arithmétiques de Bordeaux, Conf., Université de Bordeaux, Bordeaux, 1974, Astérisque, vols. 24–25 (Société Mathématique de France, Paris, 1975), 119–131 (in French); MR 0376534.Google Scholar
Benois, D., A generalization of Greenberg’s ℒ-invariant , Amer. J. Math. 133 (2011), 1573–1632, doi:10.1353/ajm.2011.0043; MR 2863371.Google Scholar
Benois, D., $p$ -adic heights and $p$ -adic Hodge theory, Preprint (2014), arXiv:1412.7305.Google Scholar
Bertolini, M., Darmon, H. and Prasanna, K., Generalized Heegner cycles and p-adic Rankin L-series , Duke Math. J. 162 (2013), 1033–1148, with an appendix by Brian Conrad, doi:10.1215/00127094-2142056; MR 3053566.Google Scholar
Bertrand, D., Propriétés arithmétiques de fonctions thêta à plusieurs variables , in Number theory, Noordwijkerhout 1983, Lecture Notes in Mathematics, vol. 1068 (Springer, Berlin, 1984), 17–22 (in French), doi:10.1007/BFb0099438; MR 756080.Google Scholar
Besser, A., p-adic Arakelov theory , J. Number Theory 111 (2005), 318–371, doi:10.1016/j.jnt.2004.11.010; MR 2130113 (2006j:14029).Google Scholar
Bump, D., Automorphic forms and representations, Cambridge Studies in Advanced Mathematics, vol. 55 (Cambridge University Press, Cambridge, 1997); MR 1431508 (97k:11080).Google Scholar
Burungale, A. A., On the 𝜇-invariant of the cyclotomic derivative of a Katz p-adic L-function , J. Inst. Math. Jussieu 14 (2015), 131–148; MR 3284481.Google Scholar
Bushnell, C. J. and Henniart, G., The local Langlands conjecture for GL(2) , Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 335 (Springer, Berlin, 2006); MR 2234120 (2007m:22013).Google Scholar
Cai, L., Shu, J. and Tian, Y., Explicit Gross–Zagier and Waldspurger formulae , Algebra Number Theory 8 (2014), 2523–2572; MR 3298547.Google Scholar
Carayol, H., Sur les représentations l-adiques associées aux formes modulaires de Hilbert , Ann. Sci. Éc. Norm. Supér. (4) 19 (1986), 409–468 (in French); MR 870690 (89c:11083).CrossRefGoogle Scholar
Coleman, R. F. and Gross, B. H., p-adic heights on curves , in Algebraic number theory, Advanced Studies in Pure Mathematics, vol. 17 (Academic Press, Boston, MA, 1989), 73–81; MR 1097610 (92d:11057).Google Scholar
Conrad, B., Lifting global representations with local properties, Preprint,http://math.stanford.edu/∼conrad/.Google Scholar
Cornut, C. and Vatsal, V., CM points and quaternion algebras , Doc. Math. 10 (2005), 263–309; MR 2148077 (2006c:11069).Google Scholar
Deligne, P. and Ribet, K. A., Values of abelian L-functions at negative integers over totally real fields , Invent. Math. 59 (1980), 227–286, doi:10.1007/BF01453237; MR 579702 (81m:12019).Google Scholar
de Shalit, E., Relative Lubin–Tate groups , Proc. Amer. Math. Soc. 95 (1985), 1–4, doi:10.2307/2045561; MR 796434 (86m:11095).Google Scholar
Disegni, D., p-adic heights of Heegner points on Shimura curves , Algebra Number Theory 9 (2015), 1571–1646, doi:10.2140/ant.2015.9.1571; MR 3404649.Google Scholar
Disegni, D., On the $p$ -adic Birch and Swinnerton-Dyer conjecture for elliptic curves over number fields, Preprint (2016), arXiv:1609.02528.Google Scholar
Emerton, M., On the interpolation of systems of eigenvalues attached to automorphic Hecke eigenforms , Invent. Math. 164 (2006), 1–84, doi:10.1007/s00222-005-0448-x; MR 2207783.Google Scholar
Fouquet, O., Dihedral Iwasawa theory of nearly ordinary quaternionic automorphic forms , Compos. Math. 149 (2013), 356–416, doi:10.1112/S0010437X12000619; MR 3040744.Google Scholar
Gross, B. H., Local heights on curves , in Arithmetic geometry, Storrs, CT, 1984 (Springer, New York, 1986), 327–339; MR 861983.Google Scholar
Gross, B. H., L-functions at the central critical point, Motives, Seattle, WA, 1991, Proceedings of Symposia in Pure Mathematics, vol. 55 (American Mathematical Society, Providence, RI, 1994), 527–535; MR 1265543 (95a:11060).Google Scholar
Gross, B. H. and Zagier, D. B., Heegner points and derivatives of L-series , Invent. Math. 84 (1986), 225–320, doi:10.1007/BF01388809; MR 833192 (87j:11057).CrossRefGoogle Scholar
Hida, H., On p-adic L-functions of GL(2) × GL(2) over totally real fields , Ann. Inst. Fourier (Grenoble) 41 (1991), 311–391, in English, with French summary; MR 1137290 (93b:11052).Google Scholar
Hida, H., The Iwasawa 𝜇-invariant of p-adic Hecke L-functions , Ann. of Math. (2) 172 (2010), 41–137, doi:10.4007/annals.2010.172.41; MR 2680417 (2012d:11215).CrossRefGoogle Scholar
Howard, B., The Iwasawa theoretic Gross–Zagier theorem , Compos. Math. 141 (2005), 811–846, doi:10.1112/S0010437X0500134X; MR 2148200 (2006f:11074).Google Scholar
Hsieh, M.-L., On the 𝜇-invariant of anticyclotomic p-adic L-functions for CM fields , J. reine angew. Math. 688 (2014), 67–100, doi:10.1515/crelle-2012-0056; MR 3176616.Google Scholar
Hu, Y., Cuspidal part of an Eisenstein series restricted to an index 2 subfield , Res. Number Theory 2 (2016), Art. 33, 61, doi:10.1007/s40993-016-0061-7; MR 3575841.Google Scholar
Iovita, A. and Werner, A., p-adic height pairings on abelian varieties with semistable ordinary reduction , J. reine angew. Math. 564 (2003), 181–203, doi:10.1515/crll.2003.089; MR 2021039 (2004j:11066).Google Scholar
Jacquet, H. and Langlands, R. P., Automorphic forms on GL(2), Lecture Notes in Mathematics, vol. 114 (Springer, Berlin–New York, 1970), MR 0401654 (53 #5481).Google Scholar
Kobayashi, S., The p-adic Gross–Zagier formula for elliptic curves at supersingular primes , Invent. Math. 191 (2013), 527–629, doi:10.1007/s00222-012-0400-9; MR 3020170.Google Scholar
Le Hung, B., Modularity of some elliptic curves over totally real fields, PhD thesis, Harvard University (2014), http://math.uchicago.edu/∼lhvietbao/.Google Scholar
Liu, Y., Zhang, S.-W. and Zhang, W., On $p$ -adic Waldspurger formula, Preprint (2015),arXiv:1511.08172.Google Scholar
Ma, L., $p$ -adic Gross–Zagier formula for Heegner points on Shimura curves over totally real fields, Preprint (2016), arXiv:1601.06996.Google Scholar
Mazur, B., Modular curves and arithmetic , in Proceedings of the International Congress of Mathematicians, Vols. 1, 2, Warsaw, 1983 (PWN, Warsaw, 1984), 185–211; MR 804682 (87a:11054).Google Scholar
Mazur, B. and Tate, J., Canonical height pairings via biextensions , in Arithmetic and geometry, Vol. I, Progress in Mathematics, vol. 35 (Birkhäuser, Boston, MA, 1983), 195–237; MR 717595 (85j:14081).Google Scholar
Mokrane, A., La suite spectrale des poids en cohomologie de Hyodo–Kato , Duke Math. J. 72 (1993), 301–337 (in French), doi:10.1215/S0012-7094-93-07211-0; MR 1248675 (95a:14022).Google Scholar
Nekovář, J., On p-adic height pairings , in Séminaire de théorie des nombres, Paris, 1990–91, Progress in Mathematics, vol. 108 (Birkhäuser, Boston, MA, 1993), 127–202; MR 1263527 (95j:11050).Google Scholar
Nekovář, J., On the p-adic height of Heegner cycles , Math. Ann. 302 (1995), 609–686, doi:10.1007/BF01444511; MR 1343644 (96f:11073).Google Scholar
Nekovář, J., Selmer complexes , Astérisque 310 (2006), in English, with English and French summaries; MR 2333680 (2009c:11176).Google Scholar
Perrin-Riou, B., Points de Heegner et dérivées de fonctions L p-adiques , Invent. Math. 89 (1987), 455–510, doi:10.1007/BF01388982 (in French); MR 903381 (89d:11034).CrossRefGoogle Scholar
Perrin-Riou, B., Fonctions L p-adiques, théorie d’Iwasawa et points de Heegner , Bull. Soc. Math. France 115 (1987), 399–456 (in French, with English summary); MR 928018 (89d:11094).Google Scholar
Pottharst, J. and Xiao, L., On the parity conjecture in finite-slope families, Preprint (2014),arXiv:1410.5050.Google Scholar
Rapoport, M., Compactifications de l’espace de modules de Hilbert–Blumenthal , Compos. Math. 36 (1978), 255–335 (in French); MR 515050 (80j:14009).Google Scholar
Rohrlich, D. E., On L-functions of elliptic curves and anticyclotomic towers , Invent. Math. 75 (1984), 383–408, doi:10.1007/BF01388635; MR 735332 (86g:11038a).Google Scholar
Saito, H., On Tunnell’s formula for characters of GL(2) , Compos. Math. 85 (1993), 99–108; MR 1199206 (93m:22021).Google Scholar
Schneider, P., p-adic height pairings. I , Invent. Math. 69 (1982), 401–409,doi:10.1007/BF01389362; MR 679765 (84e:14034).Google Scholar
Schneider, P., p-adic height pairings. II , Invent. Math. 79 (1985), 329–374, doi:10.1007/BF01388978; MR 778132 (86j:11063).Google Scholar
Serre, J.-P., Abelian l-adic representations and elliptic curves , in McGill University lecture notes written with the collaboration of Willem Kuyk and John Labute (W. A. Benjamin, New York–Amsterdam, 1968); MR 0263823 (41 #8422).Google Scholar
Shnidman, A., p-adic heights of generalized Heegner cycles , Ann. Inst. Fourier (Grenoble) 66 (2016), 1117–1174 (in English, with English and French summaries); MR 3494168.Google Scholar
Tian, Y., Yuan, X. and Zhang, S.-W., Genus periods, genus points and congruent number problem, Preprint (2014), arXiv:1411.4728.Google Scholar
Tunnell, J. B., Local 𝜖-factors and characters of GL(2) , Amer. J. Math. 105 (1983), 1277–1307, doi:10.2307/2374441; MR 721997 (86a:22018).Google Scholar
Van Order, J., On the quaternionic p-adic L-functions associated to Hilbert modular eigenforms , Int. J. Number Theory 8 (2012), 1005–1039, doi:10.1142/S1793042112500601; MR 2926558.Google Scholar
Waldspurger, J.-L., Sur les valeurs de certaines fonctions L automorphes en leur centre de symétrie , Compos. Math. 54 (1985), 173–242 (in French); MR 783511 (87g:11061b).Google Scholar
Wan, X., Heegner point Kolyvagin system and Iwasawa main conjecture, Preprint (2014),arXiv:1408.4043.Google Scholar
Wan, X., The Iwasawa main conjecture for Hilbert modular forms , Forum Math. Sigma 3 (2015), e18 95, doi:10.1017/fms.2015.16; MR 3482263.Google Scholar
Yuan, X., Zhang, S.-W. and Zhang, W., The Gross–Kohnen–Zagier theorem over totally real fields , Compos. Math. 145 (2009), 1147–1162, doi:10.1112/S0010437X08003734; MR 2551992 (2011e:11109).Google Scholar
Yuan, X., Zhang, S.-W. and Zhang, W., The Gross–Zagier formula on Shimura curves, Annals of Mathematics Studies, vol. 184 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Zhang, S.-W., Heights of Heegner points on Shimura curves , Ann. of Math. (2) 153 (2001), 27–147, doi:10.2307/2661372; MR 1826411 (2002g:11081).Google Scholar
Zhang, S.-W., Gross–Zagier formula for GL2 , Asian J. Math. 5 (2001), 183–290; MR 1868935 (2003k:11101).Google Scholar
Zhang, S.-W., Gross–Zagier formula for GL(2) II , in Heegner points and Rankin L-series, Mathematical Sciences Research Institute Publications, vol. 49 (Cambridge University Press, Cambridge, 2004), 191–214, doi:10.1017/CBO9780511756375.008; MR 2083213 (2005k:11121).Google Scholar