Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T04:44:33.507Z Has data issue: false hasContentIssue false
  • English
  • Français

On the minimal ramification problem for ℓ-groups

Part of: Algebraic number theory: global fields Representation theory of groups

Published online by Cambridge University Press:  18 March 2010

Hershy Kisilevsky  and
Jack Sonn
Hershy Kisilevsky
Affiliation:
Department of Mathematics and Statistics, Concordia University, Montreal, Quebec H3G 1M8, Canada (email: [email protected])
Jack Sonn
Affiliation:
Department of Mathematics, Technion, 32000 Haifa, Israel (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ℓ be a prime number. It is not known whether every finite ℓ-group of rank n≥1 can be realized as a Galois group over 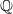with no more than n ramified primes. We prove that this can be done for the (minimal) family of finite ℓ-groups which contains all the cyclic groups of ℓ-power order and is closed under direct products, (regular) wreath products and rank-preserving homomorphic images. This family contains the Sylow ℓ-subgroups of the symmetric groups and of the classical groups over finite fields of characteristic not ℓ. On the other hand, it does not contain all finite ℓ-groups.

Keywords

Galois groupp-groupramified primeswreath productsemiabelian group

MSC classification

Secondary: 11R32: Galois theory 20D15: Nilpotent groups, $p$-groups
Type
Research Article
Information
Compositio Mathematica , Volume 146 , Issue 3 , May 2010 , pp. 599 - 606
Copyright
Copyright © Foundation Compositio Mathematica 2010

References

[1]Dentzer, R., On geometric embedding problems and semiabelian groups, Manuscripta Math. 86 (1995), 199–216.CrossRefGoogle Scholar
[2]Johnson, C. E. and Zassenhaus, H., On equivalence of finite group extensions, Math. Z. 123 (1971), 191–200.CrossRefGoogle Scholar
[3]Kaloujnine, L., La structure des p-groupes de Sylow des groupes symetriques finis, Ann. Sci École Norm. Sup. (3) 65 (1948), 239–276.CrossRefGoogle Scholar
[4]Kisilevsky, H. and Sonn, J., Abelian extensions of global fields with constant local degrees, Math. Res. Lett. 13 (2006), 599–605.CrossRefGoogle Scholar
[5]Neftin, D., On semiabelian p-groups, Preprint, arXiv:0908.1472v2 [math.gr].Google Scholar
[6]Nomura, A., Notes on the minimal number of ramified primes in some l-extensions of , Arch. Math. 90 (2008), 501–510.CrossRefGoogle Scholar
[7]Plans, B., On the minimal number of ramified primes in some solvable extensions of , Pacific J. Math. 215 (2004), 381–391.CrossRefGoogle Scholar
[8]Ribes, L. and Wong, K., On the minimal number of generators of certain groups, in Groups St Andrews 1989, London Mathematical Society Lecture Note Series, vol. 159–160 (Cambridge University Press, Cambridge, 1991).Google Scholar
[9]Schneps, L., Reduction of p-groups, Comm. Algebra 21 (1993), 1603–1609.CrossRefGoogle Scholar
[10]Serre, J.-P., Topics in Galois theory (Jones and Bartlett, Boston, 1992).Google Scholar
[11]Weir, A. J., Sylow p-subgroups of the classical groups over finite fields with characteristic prime to p, Proc. Amer. Math. Soc. 6 (1955), 529–533.Google Scholar