Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-20T12:43:08.377Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Kohnen plus space for Hilbert modular forms of half-integral weight I

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  06 September 2013

Kaoru Hiraga  and
Tamotsu Ikeda
Kaoru Hiraga
Affiliation:
Graduate School of Mathematics, Kyoto University, Kitashirakawa, Kyoto, 606-8502, Japan email [email protected]@math.kyoto-u.ac.jp
Tamotsu Ikeda
Affiliation:
Graduate School of Mathematics, Kyoto University, Kitashirakawa, Kyoto, 606-8502, Japan email [email protected]@math.kyoto-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

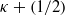In this paper, we construct a generalization of the Kohnen plus space for Hilbert modular forms of half-integral weight. The Kohnen plus space can be characterized by the eigenspace of a certain Hecke operator. It can be also characterized by the behavior of the Fourier coefficients. For example, in the parallel weight case, a modular form of weight $\kappa + (1/ 2)$ with 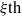$\xi \mathrm{th} $ Fourier coefficient 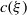$c(\xi )$ belongs to the Kohnen plus space if and only if 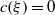$c(\xi )= 0$ unless 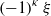$\mathop{(- 1)}\nolimits ^{\kappa } \xi $ is congruent to a square modulo 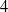$4$. The Kohnen subspace is isomorphic to a certain space of Jacobi forms. We also prove a generalization of the Kohnen–Zagier formula.

Keywords

Hilbert modular formsmodular forms of half-integral weightKohnen plus spaceJacobi forms

MSC classification

Secondary: 11F37: Forms of half-integer weight; nonholomorphic modular forms 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11F30: Fourier coefficients of automorphic forms 11F50: Jacobi forms 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 12 , December 2013 , pp. 1963 - 2010
Copyright
© The Author(s) 2013 

References

Baruch, E. and Mao, Z., Central value of automorphic L-functions, Geom. Funct. Anal. 17 (2007), 333–384.CrossRefGoogle Scholar
Berndt, R. and Schmidt, R., Elements of the Representation Theory of the Jacobi Group, Progress in Mathematics, vol. 163 (Birkhäuser, Basel, 1998).Google Scholar
Blasius, D., Hilbert modular forms and the Ramanujan conjecture, in Noncommutative Geometry and Number Theory, Aspects of Mathematics, vol. E37 (Vieweg, Wiesbaden, 2006), 35–56.Google Scholar
Bump, D., Friedberg, S. and Hoffstein, J., Eisenstein series on the metaplectic group and nonvanishing theorems for automorphic L-functions and their derivatives, Ann. of Math. (2) 131 (1990), 53–127.Google Scholar
Bump, D., Friedberg, S. and Hoffstein, J., p-adic Whittaker functions on the metaplectic group, Duke Math. J. 63 (1991), 379–397.Google Scholar
Eichler, M. and Zagier, D., The Theory of Jacobi forms, Progress in Mathematics, vol. 55 (Birkhäuser, Boston, MA, 1985).Google Scholar
Feigon, B., Lapid, E. and Offen, O., On representations distinguished by unitary groups, Publ. Math. Inst. Hautes Études Sci. 115 (2012), 185–323.Google Scholar
Friedberg, S. and Hoffstein, J., Non-vanishing theorems for automorphic L-functions on GL(2), Ann. of Math. (2) 142 (1995), 385–423.Google Scholar
van der Geer, G., Hilbert Modular Surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 16 (Springer, Berlin, 1988).Google Scholar
Hijikata, H., Pizer, A. and Shemanke, T., Orders in quaternion algebras, J. Reine Angew. Math. 394 (1989), 59–106.Google Scholar
Ichino, A., Pullbacks of Saito-Kurokawa lifts, Invent. Math. 162 (2005), 551–647.Google Scholar
Ikeda, T., On the theory of Jacobi forms and Fourier–Jacobi coefficients of Eisenstein series, J. Math. Kyoto Univ. 34 (1994), 615–636.Google Scholar
Ikeda, T., On the lifting of elliptic cusp forms to Siegel cusp forms of degree $2n$, Ann. of Math. (2) 154 (2001), 641–682.Google Scholar
Jacquet, H., Automorphic Forms on GL(2). Part II, Lecture Notes in Mathematics, vol. 278 (Springer, Berlin, 1972).Google Scholar
Kohnen, W., Modular forms of half-integral weight on ${\Gamma }_{0} (4)$, Math. Ann. 248 (1980), 249–266.Google Scholar
Kohnen, W. and Zagier, D., Values of $L$-series of modular forms at the center of the critical strip, Invent. Math. 64 (1981), 175–198.Google Scholar
Kojima, H., On the Fourier coefficients of Jacobi forms of index $N$ over totally real number fields, Tohoku Math. J. (2) 64 (2012), 361–385.CrossRefGoogle Scholar
Li, W.-W., Transfert d’intégrales orbitales pour le groupe métapectique, Compositio Math. 147 (2011), 524–590.Google Scholar
Loke, H. Y. and Savin, G., Representations of the two-fold central extension of ${\mathrm{SL} }_{2} ({ \mathbb{Q} }_{2} )$, Pacific J. Math. 247 (2010), 435–454.CrossRefGoogle Scholar
Okazaki, R., On evaluation of L-functions over real quadratic fields, J. Math. Kyoto Univ. 31 (1991), 1125–1153.Google Scholar
O’Meara, O. T., Introduction to Quadratic Forms (Reprint of the 1973 Edition) (Springer, Berlin, 2000).Google Scholar
Schmidt, R., Spherical representations of the Jacobi groups, Abh. Math. Semin. Univ. Hambg. 68 (1998), 273–296.Google Scholar
Shimura, G., On modular forms of half integral weight, Ann. of Math. (2) 97 (1973), 440–481.Google Scholar
Shimura, G., On Eisenstein series of half-integral weight, Duke Math. J. 52 (1985), 281–314.CrossRefGoogle Scholar
Shimura, G., On Hilbert modular forms of half-integral weight, Duke Math. J. 55 (1987), 765–838.Google Scholar
Shimura, G., On the Fourier coefficients of Hilbert modular forms of half-integral weight, Duke Math. J. 71 (1993), 501–557.Google Scholar
Tate, J., Number theoretic background, in Automorphic forms, representations and L-functions, Proceedings of Symposia in Pure Mathematics, vol. 33, Part 2 (American Mathematical Society, Providence, RI, 1979), 3–26.Google Scholar
Ueda, M., On twisting operators and newforms of half-integral weight, Nagoya Math. J. 131 (1993), 135–205.Google Scholar
Ueda, M., On twisting operators and newforms of half-integral weight II: complete theory of newforms for Kohnen space, Nagoya Math. J. 149 (1998), 117–171.Google Scholar
Waldspurger, J.-L., Correspondance de Shimura, J. Math. Pures Appl. (9) 59 (1980), 1–132.Google Scholar
Waldspurger, J.-L., Sur les coefficients de Fourier des formes modulaires de poids demi-entier, J. Math. Pures Appl. (9) 60 (1981), 375–484.Google Scholar
Waldspurger, J.-L., Correspondances de Shimura et quaternions, Forum Math. 3 (1991), 219–307.Google Scholar
Weil, A., Sur certains groupes d’opérateurs unitaires, Acta Math. 111 (1964), 143–211.CrossRefGoogle Scholar