Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T04:41:02.439Z Has data issue: false hasContentIssue false
  • English
  • Français

On the de Rham homology and cohomology of a complete local ring in equicharacteristic zero

Part of: (Co)homology theory Commutative algebra: Homological methods

Published online by Cambridge University Press:  07 August 2017

Nicholas Switala
Nicholas Switala*
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, 322 SEO (M/C 249), 851 S. Morgan Street, Chicago, IL 60607, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 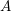$A$ be a complete local ring with a coefficient field 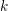$k$ of characteristic zero, and let 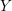$Y$ be its spectrum. The de Rham homology and cohomology of 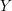$Y$ have been defined by R. Hartshorne using a choice of surjection 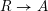$R\rightarrow A$ where 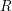$R$ is a complete regular local 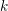$k$-algebra: the resulting objects are independent of the chosen surjection. We prove that the Hodge–de Rham spectral sequences abutting to the de Rham homology and cohomology of 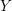$Y$, beginning with their 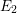$E_{2}$-terms, are independent of the chosen surjection (up to a degree shift in the homology case) and consist of finite-dimensional 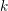$k$-spaces. These 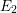$E_{2}$-terms therefore provide invariants of 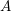$A$ analogous to the Lyubeznik numbers. As part of our proofs we develop a theory of Matlis duality in relation to 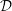${\mathcal{D}}$-modules that is of independent interest. Some of the highlights of this theory are that if 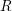$R$ is a complete regular local ring containing 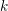$k$ and 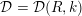${\mathcal{D}}={\mathcal{D}}(R,k)$ is the ring of 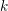$k$-linear differential operators on 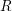$R$, then the Matlis dual 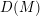$D(M)$ of any left 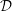${\mathcal{D}}$-module 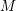$M$ can again be given a structure of left 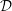${\mathcal{D}}$-module, and if 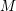$M$ is a holonomic 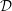${\mathcal{D}}$-module, then the de Rham cohomology spaces of 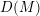$D(M)$ are 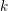$k$-dual to those of 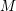$M$.

Keywords

local cohomologyalgebraic de Rham cohomologyMatlis dualityD-modules

MSC classification

Primary: 13D45: Local cohomology 14F40: de Rham cohomology
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 10 , October 2017 , pp. 2075 - 2146
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atiyah, M. and Macdonald, I., Introduction to commutative algebra (Addison-Wesley, Reading, 1969).Google Scholar
Björk, J.-E., Rings of differential operators, North-Holland Mathematical Library, vol. 21 (North-Holland Publishing, Amsterdam–New York, 1979).Google Scholar
Brodmann, M. and Sharp, R., Local cohomology, Cambridge Studies in Advanced Mathematics, vol. 136, second edition (Cambridge University Press, Cambridge, 2013).Google Scholar
Eisenbud, D., Commutative algebra with a view toward algebraic geometry, Graduate Texts in Mathematics, vol. 150 (Springer, New York, 1995).Google Scholar
Grothendieck, A., Sur quelques points d’algèbre homologique , Tohoku Math. J. (2) 9 (1957), 119–221.Google Scholar
Grothendieck, A. and Dieudonné, J., Eléments de géométrie algébrique III: Étude cohomologique des faisceaux cohérents, première partie , Publ. Math. Inst. Hautes Études Sci. 11 (1961), 5–167.Google Scholar
Grothendieck, A. and Dieudonné, J., Eléments de géométrie algébrique IV: Étude locale des schémas et des morphismes de schémas, quatrième partie , Publ. Math. Inst. Hautes Études Sci. 32 (1967), 5–361.Google Scholar
Grothendieck, A. and Raynaud, M., Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2), Documents Mathématiques, vol. 4 (Société Mathématique de France, Paris, 2005).Google Scholar
Hartshorne, R., Residues and duality, Springer Lecture Notes in Mathematics, vol. 20 (Springer, Berlin, 1966).Google Scholar
Hartshorne, R., Local cohomology, Springer Lecture Notes in Mathematics, vol. 41 (Springer, Berlin, 1967).Google Scholar
Hartshorne, R., On the de Rham cohomology of algebraic varieties , Publ. Math. Inst. Hautes Études Sci. 45 (1975), 5–99.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).Google Scholar
Hellus, M., Local cohomology and Matlis duality, habilitation thesis, University of Leipzig (2007).Google Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., D-modules, perverse sheaves, and representation theory, Progress in Mathematics, vol. 236 (Birkhäuser, Boston, 2008).Google Scholar
Kunz, E., Residues and duality for projective algebraic varieties, University Lecture Series, vol. 47 (American Mathematical Society, Providence, 2008).CrossRefGoogle Scholar
Lang, S., Algebra, Graduate Texts in Mathematics, vol. 211, revised third edition (Springer, New York, 2002).CrossRefGoogle Scholar
Lyubeznik, G., Finiteness properties of local cohomology modules , Invent. Math. 113 (1993), 41–55.Google Scholar
Lyubeznik, G., On some local cohomology invariants of local rings , Math. Z. 254 (2006), 627–640.Google Scholar
Matlis, E., Injective modules over Noetherian rings , Pacific J. Math. 8 (1958), 511–528.Google Scholar
Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8 (Cambridge University Press, Cambridge, 1986).Google Scholar
Mebkhout, Z., Local cohomology of analytic spaces , Publications of the Research Institute for Mathematical Sciences 12 (1977), 247–256.CrossRefGoogle Scholar
Núñez-Betancourt, L. and Witt, E., Generalized Lyubeznik numbers , Nagoya Math. J. 215 (2014), 169–201.CrossRefGoogle Scholar
Ogus, A., Local cohomological dimension of algebraic varieties , Ann. of Math. (2) 98 (1973), 1–34.CrossRefGoogle Scholar
Rotman, J., An introduction to homological algebra, Universitext, second edition (Springer, New York, 2009).Google Scholar
Serre, J.-P., Local algebra, Springer Monographs in Mathematics (Springer, New York, 2000).Google Scholar
Sharp, R., The Cousin complex for a module over a commutative Noetherian ring , Math. Z. 112 (1969), 340–356.Google Scholar
Switala, N., Van den Essen’s theorem on the de Rham cohomology of a holonomic D-module over a formal power series ring , Expo. Math. 35 (2016), 149–165, http://dx.doi.org/10.1016/j.exmath.2016.09.002.Google Scholar
van den Essen, A., Fuchsian modules, Ph.D. thesis, Katholieke universiteit Nijmegen, 1979.Google Scholar
van den Essen, A., Le noyau de l’opérateur $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{n}}$ agissant sur un ${\mathcal{D}}_{n}$ -module, C. R. Acad. Sci. Paris Sér. A 288 (1979), 687-690.Google Scholar
van den Essen, A., Un ${\mathcal{D}}$ -module holonome tel que le conoyau de l’opérateur $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{n}}$ soit non-holonome, C. R. Acad. Sci. Paris Sér. 1 295 (1982), 455–457.Google Scholar
van den Essen, A., Le conoyau de l’opérateur $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{n}}$ agissant sur un ${\mathcal{D}}_{n}$ -module holonome, C. R. Acad. Sci. Paris Sér. 1 296 (1983), 903–906.Google Scholar
van den Essen, A., The cokernel of the operator $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{n}}$ acting on a ${\mathcal{D}}_{n}$ -module II, Compositio Math. 56 (1985), 259–269.Google Scholar
Weibel, C., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, Cambridge, 1994).Google Scholar