Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nakagane, Keita
2019.
The action of full twist on the superpolynomial for torus knots.
Topology and its Applications,
Vol. 266,
Issue. ,
p.
106841.
Abel, Michael
and
Willis, Michael
2019.
Colored Khovanov–Rozansky homology for
infinite braids.
Algebraic & Geometric Topology,
Vol. 19,
Issue. 5,
p.
2401.
Gorsky, Eugene
Hogancamp, Matthew
Mellit, Anton
and
Nakagane, Keita
2019.
Serre duality for Khovanov–Rozansky homology.
Selecta Mathematica,
Vol. 25,
Issue. 5,
Gorsky, Eugene
Mazin, Mikhail
and
Vazirani, Monica
2020.
Recursions for rational q,t-Catalan numbers.
Journal of Combinatorial Theory, Series A,
Vol. 173,
Issue. ,
p.
105237.
Cautis, Sabin
Lauda, Aaron D.
and
Sussan, Joshua
2020.
Curved Rickard complexes and link homologies.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2020,
Issue. 769,
p.
87.
Elias, Ben
Makisumi, Shotaro
Thiel, Ulrich
and
Williamson, Geordie
2020.
Introduction to Soergel Bimodules.
Vol. 5,
Issue. ,
p.
421.
Anokhina, A.
Morozov, A.
and
Popolitov, A.
2021.
Khovanov polynomials for satellites and asymptotic adjoint polynomials.
International Journal of Modern Physics A,
Vol. 36,
Issue. 34n35,
Gorsky, Eugene
Neguţ, Andrei
and
Rasmussen, Jacob
2021.
Flag Hilbert schemes, colored projectors and Khovanov-Rozansky homology.
Advances in Mathematics,
Vol. 378,
Issue. ,
p.
107542.
Mellit, Anton
2022.
Homology of torus knots.
Geometry & Topology,
Vol. 26,
Issue. 1,
p.
47.
Gorsky, Eugene
and
Hogancamp, Matthew
2022.
Hilbert schemes and y–ification of
Khovanov–Rozansky homology.
Geometry & Topology,
Vol. 26,
Issue. 2,
p.
587.
Morton, Hugh
Pokorny, Alex
and
Samuelson, Peter
2023.
The Kauffman Skein Algebra of the Torus.
International Mathematics Research Notices,
Vol. 2023,
Issue. 1,
p.
855.
OBLOMKOV, A.
and
ROZANSKY, L.
2023.
HOMFLY-PT HOMOLOGY OF COXETER LINKS.
Transformation Groups,
Vol. 28,
Issue. 3,
p.
1245.
Gorsky, Eugene
Kivinen, Oscar
and
Simental, José
2023.
Algebra and geometry of link homology: Lecture notes from the IHES 2021 Summer School.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 2,
p.
537.
Turner, Joshua P
2024.
Affine Springer Fibers and Generalized Haiman Ideals (with an Appendix by Eugene Gorsky and Joshua P. Turner).
International Mathematics Research Notices,
Vol. 2024,
Issue. 16,
p.
11878.
Gorsky, Eugene
Hogancamp, Matthew
and
Mellit, Anton
2024.
Tautological classes and symmetry in Khovanov–Rozansky homology.
Duke Mathematical Journal,
Vol. 173,
Issue. 13,
Chandler, Alex
and
Gorsky, Eugene
2024.
Structures in HOMFLY-PT Homology.
Experimental Mathematics,
Vol. 33,
Issue. 4,
p.
817.
Galashin, Pavel
and
Lam, Thomas
2024.
Positroids, knots, and q,t-Catalan numbers.
Duke Mathematical Journal,
Vol. 173,
Issue. 11,
González, Nicolle
Simental, José
and
Vazirani, Monica
2024.
Higher rank (𝑞,𝑡)-Catalan polynomials, affine Springer fibers, and a finite rational shuffle theorem.
Transactions of the American Mathematical Society,
Hogancamp, Matthew
Rose, David E. V.
and
Wedrich, Paul
2024.
Link splitting deformation of colored Khovanov–Rozansky homology.
Proceedings of the London Mathematical Society,
Vol. 129,
Issue. 3,
Mazorchuk, Volodymyr
2025.
Some homological properties of category O, VII.
Advances in Mathematics,
Vol. 468,
Issue. ,
p.
110201.
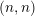 $(n,n)$-torus links, for which we give an exact answer for all
$(n,n)$-torus links, for which we give an exact answer for all  $n$. In several cases, our computations verify conjectures of Gorsky et al. relating homology of torus links with Hilbert schemes.
$n$. In several cases, our computations verify conjectures of Gorsky et al. relating homology of torus links with Hilbert schemes.