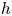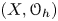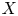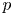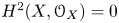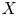1. Introduction
1.1 Frobenius-constant quantizations
For the duration of this paper, let ![]() $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic ![]() $p>2$. Given a scheme
$p>2$. Given a scheme ![]() $X$ over
$X$ over ![]() $k$ we denote by
$k$ we denote by ![]() $X'$ the Frobenius twist of
$X'$ the Frobenius twist of ![]() $X$ and by
$X$ and by ![]() $F: X\to X'$ the
$F: X\to X'$ the ![]() $k$-linear Frobenius morphism. Since
$k$-linear Frobenius morphism. Since ![]() $F$ is a homeomorphism on the underlying topological spaces, we shall identify the categories of sheaves on
$F$ is a homeomorphism on the underlying topological spaces, we shall identify the categories of sheaves on ![]() $X$ and
$X$ and ![]() $X'$.
$X'$.
Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $k$ equipped with a symplectic
$k$ equipped with a symplectic ![]() $2$-form
$2$-form ![]() $\omega$. Recall, that a quantization
$\omega$. Recall, that a quantization ![]() $(X, {\mathcal {O}}_h)$ of
$(X, {\mathcal {O}}_h)$ of ![]() $(X, \omega )$ is a sheaf
$(X, \omega )$ is a sheaf ![]() ${\mathcal {O}}_h$ on the Zariski site of
${\mathcal {O}}_h$ on the Zariski site of ![]() $X$ of flat
$X$ of flat ![]() $k[[h]]$-algebras complete with respect to the
$k[[h]]$-algebras complete with respect to the ![]() $h$-adic topology together with an isomorphism of
$h$-adic topology together with an isomorphism of ![]() $k$-algebras
$k$-algebras
such that, for any two local sections ![]() $\tilde {f}$,
$\tilde {f}$, ![]() $\tilde {g}$ of
$\tilde {g}$ of ![]() ${\mathcal {O}}_h$, one has
${\mathcal {O}}_h$, one has
Here ![]() $f$ and
$f$ and ![]() $g$ stand for the images in
$g$ stand for the images in ![]() ${\mathcal {O}}_X$ of
${\mathcal {O}}_X$ of ![]() $\tilde {f}$ and
$\tilde {f}$ and ![]() $\tilde {g}$ respectively and
$\tilde {g}$ respectively and ![]() $\{, \}$ for the Poisson bracket
$\{, \}$ for the Poisson bracket ![]() ${\mathcal {O}}_X$ induced by the symplectic structure. Note that if
${\mathcal {O}}_X$ induced by the symplectic structure. Note that if ![]() $X$ is affine then giving a quantization
$X$ is affine then giving a quantization ![]() $(X, {\mathcal {O}}_h)$ of
$(X, {\mathcal {O}}_h)$ of ![]() $(X, \omega )$ is equivalent to giving a quantization
$(X, \omega )$ is equivalent to giving a quantization ![]() ${\mathcal {O}}_h(X)$ of the Poisson algebra
${\mathcal {O}}_h(X)$ of the Poisson algebra ![]() ${\mathcal {O}}_X(X)$ (see e.g. [Reference Bezrukavnikov and KaledinBK04a, Remark 1.6]).
${\mathcal {O}}_X(X)$ (see e.g. [Reference Bezrukavnikov and KaledinBK04a, Remark 1.6]).
A feature special to characteristic ![]() $p$ is that the Poisson algebra
$p$ is that the Poisson algebra ![]() ${\mathcal {O}}_X$ of a symplectic variety has a large center consisting of
${\mathcal {O}}_X$ of a symplectic variety has a large center consisting of ![]() $p$th powers of functions. We are going to identify it with the sheaf
$p$th powers of functions. We are going to identify it with the sheaf ![]() ${\mathcal {O}}_{X'}$ using the Frobenius morphism
${\mathcal {O}}_{X'}$ using the Frobenius morphism
Given a quantization ![]() $(X, {\mathcal {O}}_h)$ of
$(X, {\mathcal {O}}_h)$ of ![]() $(X, \omega )$ we have
$(X, \omega )$ we have ![]() $k$-linear homomorphisms
$k$-linear homomorphisms
from the center ![]() ${\mathcal {Z}}_h$ of the quantization
${\mathcal {Z}}_h$ of the quantization ![]() ${\mathcal {O}}_h$ to the Poisson center. Following [Reference Bezrukavnikov and KaledinBK08], a quantization is called central if the composition (1.1) is surjective. A Frobenius-constant quantization of
${\mathcal {O}}_h$ to the Poisson center. Following [Reference Bezrukavnikov and KaledinBK08], a quantization is called central if the composition (1.1) is surjective. A Frobenius-constant quantization of ![]() $(X, \omega )$ is a pair consisting of a quantization
$(X, \omega )$ is a pair consisting of a quantization ![]() $(X, {\mathcal {O}}_h)$ of the symplectic variety
$(X, {\mathcal {O}}_h)$ of the symplectic variety ![]() $X$ together with a
$X$ together with a ![]() $k[[h]]$-algebra isomorphism
$k[[h]]$-algebra isomorphism
such that, for any local section ![]() $f^p \in {\mathcal {O}}_{X}^p = {\mathcal {O}}_{X'} \subset {\mathcal {O}}_{X'}[[h]]$ and a lift
$f^p \in {\mathcal {O}}_{X}^p = {\mathcal {O}}_{X'} \subset {\mathcal {O}}_{X'}[[h]]$ and a lift ![]() $\tilde {f}\in {\mathcal {O}}_h$ of
$\tilde {f}\in {\mathcal {O}}_h$ of ![]() $f\in {\mathcal {O}}_X$, one has thatFootnote 1
$f\in {\mathcal {O}}_X$, one has thatFootnote 1
It is clear that a quantization that admits a Frobenius-constant structure is central.
A Frobenius-constant structure on ![]() $(X, {\mathcal {O}}_h)$ makes
$(X, {\mathcal {O}}_h)$ makes ![]() ${\mathcal {O}}_h$ into a sheaf of algebras over
${\mathcal {O}}_h$ into a sheaf of algebras over ![]() ${\mathcal {O}}_{X'}[[h]]$. It was shown in [Reference Bezrukavnikov and KaledinBK08] that
${\mathcal {O}}_{X'}[[h]]$. It was shown in [Reference Bezrukavnikov and KaledinBK08] that ![]() ${\mathcal {O}}_h$ is locally free of rank
${\mathcal {O}}_h$ is locally free of rank ![]() $p^{\dim X}$ as an
$p^{\dim X}$ as an ![]() ${\mathcal {O}}_{X'}[[h]]$-module for the Zariski topology on
${\mathcal {O}}_{X'}[[h]]$-module for the Zariski topology on ![]() $X'$.
$X'$.
Frobenius-constant quantizations of symplectic varieties have been first introduced by Bezrukavnikov and Kaledin as a tool for proving the categorical McKay correspondence for symplectic resolutions of singularities (see [Reference Bezrukavnikov and KaledinBK04b]). Most of the foundational results have been obtained in [Reference Bezrukavnikov and KaledinBK08]. The technique introduced in [Reference Bezrukavnikov and KaledinBK04b] has found some other applications in geometric representations theory (see e.g. [Reference Bezrukavnikov and FinkelbergBF14, Reference Bezrukavnikov and LosevBL21]). A key to all these applications is the Azumaya property of the algebra ![]() ${\mathcal {O}}_h(h^{-1})$ obtained from
${\mathcal {O}}_h(h^{-1})$ obtained from ![]() ${\mathcal {O}}_h$ by inverting
${\mathcal {O}}_h$ by inverting ![]() $h$: it was shown in [Reference Bezrukavnikov and KaledinBK08] that for any Frobenius-constant quantization on
$h$: it was shown in [Reference Bezrukavnikov and KaledinBK08] that for any Frobenius-constant quantization on ![]() $(X, {\mathcal {O}}_h)$, the algebra
$(X, {\mathcal {O}}_h)$, the algebra ![]() ${\mathcal {O}}_h(h^{-1})$ is isomorphic, that is locally, for the fppf topology on
${\mathcal {O}}_h(h^{-1})$ is isomorphic, that is locally, for the fppf topology on ![]() $X'$, to a matrix algebra over
$X'$, to a matrix algebra over ![]() ${\mathcal {O}}_{X'}((h))$. Since the algebra
${\mathcal {O}}_{X'}((h))$. Since the algebra ![]() ${\mathcal {O}}_h$ has no zero divisors
${\mathcal {O}}_h$ has no zero divisors ![]() ${\mathcal {O}}_h(h^{-1})$ does not split even locally for the étale topology on
${\mathcal {O}}_h(h^{-1})$ does not split even locally for the étale topology on ![]() $X'$ (unless
$X'$ (unless ![]() $\dim X =0$). In [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24] a formula for the class of this Azumaya algebra in an appropriate Brauer group was proposed. However, it has been observed in [Reference MolokovMol17] that the formula in [Reference Bezrukavnikov and KaledinBK08] is not correct as stated. The immediate goal of this paper is to correct it. The technique introduced along its proof (in particular, the Basic Lemma from § 1.8) plays an essential role in a sequel paper joint with Kubrak and Travkin [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22], where we prove that the category of quasi-coherent sheaves on any restricted symplectic variety admits a canonical Frobenius-constant quantization.
$\dim X =0$). In [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24] a formula for the class of this Azumaya algebra in an appropriate Brauer group was proposed. However, it has been observed in [Reference MolokovMol17] that the formula in [Reference Bezrukavnikov and KaledinBK08] is not correct as stated. The immediate goal of this paper is to correct it. The technique introduced along its proof (in particular, the Basic Lemma from § 1.8) plays an essential role in a sequel paper joint with Kubrak and Travkin [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22], where we prove that the category of quasi-coherent sheaves on any restricted symplectic variety admits a canonical Frobenius-constant quantization.
1.2 Differential operators as a Frobenius-constant quantization
A basic example of a Frobenius-constant quantization is as follows. Let ![]() $Y$ be a smooth variety over
$Y$ be a smooth variety over ![]() $k$,
$k$, ![]() $X:= {\mathbb {T}}^*_Y$ the cotangent bundle to
$X:= {\mathbb {T}}^*_Y$ the cotangent bundle to ![]() $Y$ equipped with the canonical symplectic structure
$Y$ equipped with the canonical symplectic structure ![]() $\omega$. Denote by
$\omega$. Denote by ![]() $D_{Y}$ the sheaf of differential operators on
$D_{Y}$ the sheaf of differential operators on ![]() $Y$. This comes with a filtration given by the order of a differential operator. Applying the Rees construction to the filtered algebra
$Y$. This comes with a filtration given by the order of a differential operator. Applying the Rees construction to the filtered algebra ![]() $D_{Y}$ we obtain a sheaf of algebras
$D_{Y}$ we obtain a sheaf of algebras ![]() $D_{Y, h}$ flat over
$D_{Y, h}$ flat over ![]() $k[h]$ whose fiber over
$k[h]$ whose fiber over ![]() $h=1$ is
$h=1$ is ![]() $D_Y$ and whose fiber over
$D_Y$ and whose fiber over ![]() $h=0$ is the symmetric algebra
$h=0$ is the symmetric algebra ![]() $S^\cdot T_Y$. Explicitly,
$S^\cdot T_Y$. Explicitly, ![]() $D_{Y, h}$ is the subalgebra of
$D_{Y, h}$ is the subalgebra of ![]() $D_{Y}[h]$ generated by
$D_{Y}[h]$ generated by ![]() $h$,
$h$, ![]() ${\mathcal {O}}_Y$, and
${\mathcal {O}}_Y$, and ![]() $hT_Y$. The
$hT_Y$. The ![]() $p$-curvature homomorphism
$p$-curvature homomorphism
sending a function ![]() $f\in {\mathcal {O}}_Y$ to
$f\in {\mathcal {O}}_Y$ to ![]() $f^p$ and a vector field
$f^p$ and a vector field ![]() $\theta \in T_Y$ to
$\theta \in T_Y$ to ![]() $(h \theta )^p - h^{p-1}(h\theta ^{[p]})$ induces an isomorphism between the algebra
$(h \theta )^p - h^{p-1}(h\theta ^{[p]})$ induces an isomorphism between the algebra ![]() $S^{\cdot } T_{Y'}[h]$ and the center of
$S^{\cdot } T_{Y'}[h]$ and the center of ![]() $D_{Y, h}$. In particular,
$D_{Y, h}$. In particular, ![]() $D_{Y, h}$ can be viewed as a quasi-coherent sheaf on
$D_{Y, h}$ can be viewed as a quasi-coherent sheaf on ![]() ${\mathbb {T}}_{Y'}^*$. The canonical Frobenius-constant quantization of
${\mathbb {T}}_{Y'}^*$. The canonical Frobenius-constant quantization of ![]() $({\mathbb {T}}^*_Y, \omega )$ is obtained from
$({\mathbb {T}}^*_Y, \omega )$ is obtained from ![]() $D_{Y, h}$ by
$D_{Y, h}$ by ![]() $h$-completion. We shall denote this canonical Frobenius-constant quantization of
$h$-completion. We shall denote this canonical Frobenius-constant quantization of ![]() $({\mathbb {T}}^*_Y, \omega )$ by
$({\mathbb {T}}^*_Y, \omega )$ by ![]() $({\mathbb {T}}^*_Y, {\mathcal {D}}_{Y, h})$.
$({\mathbb {T}}^*_Y, {\mathcal {D}}_{Y, h})$.
1.3 Restricted Poisson structures
There is a local obstruction to the existence of a central quantization of a symplectic variety ![]() $(X, \omega )$. It was observed in [Reference Bezrukavnikov and KaledinBK08] that if
$(X, \omega )$. It was observed in [Reference Bezrukavnikov and KaledinBK08] that if ![]() $f^p \in {\mathcal {O}}_{X'} \buildrel {\sim }\over {\longrightarrow } {\mathcal {O}}_{X}^p$ is in the image (1.1), then the restricted power
$f^p \in {\mathcal {O}}_{X'} \buildrel {\sim }\over {\longrightarrow } {\mathcal {O}}_{X}^p$ is in the image (1.1), then the restricted power ![]() $H_f^{[p]}$ of the Hamiltonian vector field
$H_f^{[p]}$ of the Hamiltonian vector field ![]() $H_f$ is again Hamiltonian:
$H_f$ is again Hamiltonian: ![]() $H_f^{[p]}= H_{f^{[p]}}$ for some
$H_f^{[p]}= H_{f^{[p]}}$ for some ![]() $f^{[p]}\in {\mathcal {O}}_{X}$. For example, it follows that the torus
$f^{[p]}\in {\mathcal {O}}_{X}$. For example, it follows that the torus ![]() $({\mathbb {G}}_m \times {\mathbb {G}}_m, \omega = {{d}x}/{x}\wedge {{d}y}/{y})$ does not admit central quantizations.
$({\mathbb {G}}_m \times {\mathbb {G}}_m, \omega = {{d}x}/{x}\wedge {{d}y}/{y})$ does not admit central quantizations.
A Frobenius-constant structure on ![]() $(X, {\mathcal {O}}_h)$ provides a canonical Hamiltonian for
$(X, {\mathcal {O}}_h)$ provides a canonical Hamiltonian for ![]() $H_f^{[p]}$. In fact, given a Frobenius-constant quantization
$H_f^{[p]}$. In fact, given a Frobenius-constant quantization ![]() $(X, {\mathcal {O}}_h, s)$ the formula
$(X, {\mathcal {O}}_h, s)$ the formula
defines a restricted structure on the Poisson algebra ![]() ${\mathcal {O}}_X$, that is, the structure of a restricted Lie algebra on
${\mathcal {O}}_X$, that is, the structure of a restricted Lie algebra on ![]() ${\mathcal {O}}_X$ such that
${\mathcal {O}}_X$ such that ![]() $(f^2)^{[p]}= 2 f^{[p]} f^p$ and
$(f^2)^{[p]}= 2 f^{[p]} f^p$ and ![]() $H_f^{[p]}= H_{f^{[p]}}$.Footnote 2
$H_f^{[p]}= H_{f^{[p]}}$.Footnote 2
It was shown in [Reference Bezrukavnikov and KaledinBK08] that, for every symplectic variety ![]() $(X, \omega )$, giving a restricted Poisson structure on
$(X, \omega )$, giving a restricted Poisson structure on ![]() ${\mathcal {O}}_X$ is equivalent to giving a class
${\mathcal {O}}_X$ is equivalent to giving a class
such that
In one direction, if ![]() $\eta \in \Omega ^1_X$,
$\eta \in \Omega ^1_X$, ![]() $d\eta =\omega$, then the formula
$d\eta =\omega$, then the formula
defines a restricted structure on ![]() ${\mathcal {O}}_X$. In particular, if
${\mathcal {O}}_X$. In particular, if ![]() $(X, \omega )$ admits a restricted structure, then
$(X, \omega )$ admits a restricted structure, then ![]() $\omega$ is exact locally for Zariski topology on
$\omega$ is exact locally for Zariski topology on ![]() $X$.
$X$.
1.4 Classification of Frobenius-constant quantizations
Fix a symplectic variety ![]() $X$ with a restricted Poisson structure
$X$ with a restricted Poisson structure ![]() $[\eta ]$. Denote by
$[\eta ]$. Denote by ![]() $Q(X, [\eta ])$ the set of isomorphism classes of Frobenius-constant quantizations
$Q(X, [\eta ])$ the set of isomorphism classes of Frobenius-constant quantizations ![]() $(X, {\mathcal {O}}_h, s)$ compatible with
$(X, {\mathcal {O}}_h, s)$ compatible with ![]() $[\eta ]$. In [Reference Bezrukavnikov and KaledinBK08], Bezrukavnikov and Kaledin constructed a map of sets
$[\eta ]$. In [Reference Bezrukavnikov and KaledinBK08], Bezrukavnikov and Kaledin constructed a map of sets
and showed that if ![]() $H^1_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then
$H^1_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then ![]() $\rho$ is injective, and if
$\rho$ is injective, and if ![]() $H^2_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then
$H^2_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then ![]() $\rho$ is surjective. Consequently, if both cohomology groups vanish the map
$\rho$ is surjective. Consequently, if both cohomology groups vanish the map ![]() $\rho$ is a bijection and there is a canonical Frobenius-constant quantization of
$\rho$ is a bijection and there is a canonical Frobenius-constant quantization of ![]() $(X, [\eta ])$ corresponding to
$(X, [\eta ])$ corresponding to ![]() $0\in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$. This quantization
$0\in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$. This quantization ![]() $(X, {\mathcal {O}}_h, s)$ is uniquely characterized as the one that admits a
$(X, {\mathcal {O}}_h, s)$ is uniquely characterized as the one that admits a ![]() ${\mathbb {Z}}/2$-equivariant structure: an isomorphism
${\mathbb {Z}}/2$-equivariant structure: an isomorphism ![]() ${\mathcal {O}}_{X'}[[h]]$-algebras
${\mathcal {O}}_{X'}[[h]]$-algebras
identical modulo ![]() $h$ and such that
$h$ and such that ![]() $\alpha \circ \alpha = \operatorname {Id}$. We review the construction of
$\alpha \circ \alpha = \operatorname {Id}$. We review the construction of ![]() $\rho$ in § 2.
$\rho$ in § 2.
1.5 A central reduction of the algebra of differential operators
A class
gives rise to a certain central reduction ![]() $\mathcal {D}_{X, [\eta ], h}$ of the algebra
$\mathcal {D}_{X, [\eta ], h}$ of the algebra ![]() $\mathcal {D}_{X, h}$. We first construct this reduction locally and then glue. For any open subset
$\mathcal {D}_{X, h}$. We first construct this reduction locally and then glue. For any open subset ![]() $U$ together with a
$U$ together with a ![]() $1$-form
$1$-form ![]() $\eta \in \Omega ^1(U)$ representing
$\eta \in \Omega ^1(U)$ representing ![]() $[\eta ]$, consider the graph
$[\eta ]$, consider the graph ![]() $\Gamma _{\eta }: U' \rightarrow \mathbb {T}_{U'}^*$ of
$\Gamma _{\eta }: U' \rightarrow \mathbb {T}_{U'}^*$ of ![]() $\eta \otimes 1 \in \Omega ^1 (U')$. Let
$\eta \otimes 1 \in \Omega ^1 (U')$. Let ![]() $\mathcal {D}_{U, h}$ be the quantization of
$\mathcal {D}_{U, h}$ be the quantization of ![]() $\mathbb {T}^*_{U}$ defined above regarded as a locally free sheaf of modules over
$\mathbb {T}^*_{U}$ defined above regarded as a locally free sheaf of modules over ![]() $S^{\cdot }T_{U'}[[h]]$ on
$S^{\cdot }T_{U'}[[h]]$ on ![]() $U$. Set
$U$. Set
Here ![]() $I_{\Gamma _{\eta }} \subset S^{\cdot }T_{U'}$ is sheaf of ideals defined by the closed embedding
$I_{\Gamma _{\eta }} \subset S^{\cdot }T_{U'}$ is sheaf of ideals defined by the closed embedding ![]() $\Gamma _{\eta }$. Note that
$\Gamma _{\eta }$. Note that ![]() $\Gamma _{\eta _1}^{*} \mathcal {D}_{U, h}$ is a sheaf of algebras over
$\Gamma _{\eta _1}^{*} \mathcal {D}_{U, h}$ is a sheaf of algebras over ![]() $S^{\cdot }T_{U'}/I_{\Gamma _{\eta }} [[h]]\buildrel {\sim }\over {\longrightarrow } {\mathcal {O}}_{U'}[[h]]$.
$S^{\cdot }T_{U'}/I_{\Gamma _{\eta }} [[h]]\buildrel {\sim }\over {\longrightarrow } {\mathcal {O}}_{U'}[[h]]$.
Suppose we are given two forms ![]() $\eta _1$,
$\eta _1$, ![]() $\eta _2$ on
$\eta _2$ on ![]() $U$ representing the class
$U$ representing the class ![]() $[\eta ]$. Let us construct a canonical isomorphism between the algebras
$[\eta ]$. Let us construct a canonical isomorphism between the algebras ![]() $\Gamma _{\eta _1}^{*} \mathcal {D}_{X, h}$ and
$\Gamma _{\eta _1}^{*} \mathcal {D}_{X, h}$ and ![]() $\Gamma _{\eta _2}^{*} \mathcal {D}_{X, h}$. Set
$\Gamma _{\eta _2}^{*} \mathcal {D}_{X, h}$. Set ![]() $\mu = \eta _1 - \eta _2$. Define the automorphism
$\mu = \eta _1 - \eta _2$. Define the automorphism ![]() $\phi _{\mu }$ of
$\phi _{\mu }$ of ![]() $\mathcal {D}_{X, h}$ by setting
$\mathcal {D}_{X, h}$ by setting ![]() $\phi _{\mu }(f)=f$ and
$\phi _{\mu }(f)=f$ and ![]() $\phi _{\mu }(h\theta )=h\theta + \iota _{\theta }\mu$, for any function
$\phi _{\mu }(h\theta )=h\theta + \iota _{\theta }\mu$, for any function ![]() $f$ and vector field
$f$ and vector field ![]() $\theta$.Footnote 3 Let
$\theta$.Footnote 3 Let ![]() $t_{\mu }$ be the translation by
$t_{\mu }$ be the translation by ![]() $\mu$ on
$\mu$ on ![]() $S^{\cdot }T_{U'}$ i.e. an automorphism sending a vector field
$S^{\cdot }T_{U'}$ i.e. an automorphism sending a vector field ![]() $\theta$ to
$\theta$ to ![]() $\theta + \iota _{\theta }\mu$. Then using the Katz formula [Reference KatzKat72, § 7.22] (and the exactness of
$\theta + \iota _{\theta }\mu$. Then using the Katz formula [Reference KatzKat72, § 7.22] (and the exactness of ![]() $\mu$) the following diagram is commutative.
$\mu$) the following diagram is commutative.

The desired isomorphism is given by the formula
Given three ![]() $1$-forms
$1$-forms ![]() $\eta _1$,
$\eta _1$, ![]() $\eta _2$, and
$\eta _2$, and ![]() $\eta _3$ representing the class
$\eta _3$ representing the class ![]() $[\eta ]$ one has
$[\eta ]$ one has
The sheaf of algebras ![]() $\mathcal {D}_{X, [\eta ], h}$ is obtained by gluing
$\mathcal {D}_{X, [\eta ], h}$ is obtained by gluing ![]() $\Gamma _{\eta }^{*} \mathcal {D}_{U, h}$ along the above isomorphisms.
$\Gamma _{\eta }^{*} \mathcal {D}_{U, h}$ along the above isomorphisms.
The sheaf ![]() ${\mathcal {D}}_{X, [\eta ], h}$ of
${\mathcal {D}}_{X, [\eta ], h}$ of ![]() ${\mathcal {O}}_{X'}[[h]]$-algebras is locally free as a
${\mathcal {O}}_{X'}[[h]]$-algebras is locally free as a ![]() ${\mathcal {O}}_{X'}[[h]]$-module of rank
${\mathcal {O}}_{X'}[[h]]$-module of rank ![]() $p^{2\dim X}$. The commutative algebra
$p^{2\dim X}$. The commutative algebra ![]() ${\mathcal {D}}_{X, [\eta ], h}/h$ is isomorphic to the algebra of functions on the Frobenius neighborhood of the zero section
${\mathcal {D}}_{X, [\eta ], h}/h$ is isomorphic to the algebra of functions on the Frobenius neighborhood of the zero section ![]() $X\hookrightarrow {\mathbb {T}}^*_X$ with the Poisson structure given by the symplectic form
$X\hookrightarrow {\mathbb {T}}^*_X$ with the Poisson structure given by the symplectic form ![]() $\omega _{{\rm can}} + \operatorname {pr} ^* \omega$ on
$\omega _{{\rm can}} + \operatorname {pr} ^* \omega$ on ![]() ${\mathbb {T}}^*_X$. Here
${\mathbb {T}}^*_X$. Here ![]() $\omega _{{\rm can}}$ is the canonical symplectic form on the cotangent bundle, and
$\omega _{{\rm can}}$ is the canonical symplectic form on the cotangent bundle, and ![]() $\operatorname {pr}: {\mathbb {T}}^*_X \to X$ is the projection.
$\operatorname {pr}: {\mathbb {T}}^*_X \to X$ is the projection.
Remark 1.1 The sheaf ![]() $\mathcal {D}_{X, [\eta ], h}$ is the restriction of a certain canonical locally free
$\mathcal {D}_{X, [\eta ], h}$ is the restriction of a certain canonical locally free ![]() ${\mathcal {O}}_{X^{\prime } \times {\mathbb {P}}^1}$-algebra over
${\mathcal {O}}_{X^{\prime } \times {\mathbb {P}}^1}$-algebra over ![]() $X'\times {\mathbb {P}}^1$ to the formal completion of
$X'\times {\mathbb {P}}^1$ to the formal completion of ![]() $X' \times \{0\} \hookrightarrow X'\times {\mathbb {P}}^1$ (see [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22, § 3.3]).
$X' \times \{0\} \hookrightarrow X'\times {\mathbb {P}}^1$ (see [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22, § 3.3]).
1.6 Main result
Denote by ![]() $\operatorname {Br}(X'[[h]])$ the Brauer group of the formal scheme
$\operatorname {Br}(X'[[h]])$ the Brauer group of the formal scheme ![]() $(X', {\mathcal {O}}_{X'}[[h]])$ obtained from
$(X', {\mathcal {O}}_{X'}[[h]])$ obtained from ![]() $X' \times \operatorname {Spec} k[h]$ by completion along the closed subscheme cut by the equation
$X' \times \operatorname {Spec} k[h]$ by completion along the closed subscheme cut by the equation ![]() $h=0$. We have homomorphisms:
$h=0$. We have homomorphisms:
The first map in (1.7) is the boundary morphism associated to the short exact sequence of sheaves for the étale topology
The right arrow in (1.7) is the pullback homomorphism which is a split injection because its composition with the restriction homomorphism
is the identity. Given a class ![]() $\gamma \in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$ we denote by
$\gamma \in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$ we denote by ![]() $\delta (\gamma ) \in \operatorname {Br}(X'[[h]])$ the image of
$\delta (\gamma ) \in \operatorname {Br}(X'[[h]])$ the image of ![]() $\gamma$ under the composition (1.7). Finally, we can state the main result of this paper.
$\gamma$ under the composition (1.7). Finally, we can state the main result of this paper.
Theorem 1 Let ![]() $(X, \omega )$ be a smooth symplectic variety of dimension
$(X, \omega )$ be a smooth symplectic variety of dimension ![]() $2n$ over an algebraically closed field
$2n$ over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>2$, and let
$p>2$, and let ![]() $(X, {\mathcal {O}}_h, s)$ be a Frobenius-constant quantization of
$(X, {\mathcal {O}}_h, s)$ be a Frobenius-constant quantization of ![]() $(X, \omega )$. Denote by
$(X, \omega )$. Denote by ![]() $[\eta ] \in H^0_{\rm Zar}(X, \operatorname {coker}({\mathcal {O}}_X \stackrel {d}{\longrightarrow } \Omega ^1_X))$ the restricted Poisson structure corresponding to
$[\eta ] \in H^0_{\rm Zar}(X, \operatorname {coker}({\mathcal {O}}_X \stackrel {d}{\longrightarrow } \Omega ^1_X))$ the restricted Poisson structure corresponding to ![]() $(X, {\mathcal {O}}_h, s)$ and by
$(X, {\mathcal {O}}_h, s)$ and by ![]() $\gamma = \rho (X, {\mathcal {O}}_h, s) \in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$ the image of
$\gamma = \rho (X, {\mathcal {O}}_h, s) \in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$ the image of ![]() $(X, {\mathcal {O}}_h, s)$ under (1.4). Then there exists an Azumaya algebra
$(X, {\mathcal {O}}_h, s)$ under (1.4). Then there exists an Azumaya algebra ![]() ${\mathcal {O}}^\sharp _h$ over the formal scheme
${\mathcal {O}}^\sharp _h$ over the formal scheme ![]() $(X', {\mathcal {O}}_{X'}[[h]])$ with the following properties.
$(X', {\mathcal {O}}_{X'}[[h]])$ with the following properties.
(i) There exists an isomorphism of
 ${\mathcal {O}}_{X'}((h))$-algebras
(1.8)
${\mathcal {O}}_{X'}((h))$-algebras
(1.8) \begin{equation} ({\mathcal{O}}_h \otimes_{{\mathcal{O}}_{X'}[[h]]} {\mathcal{D}}_{X, [\eta], h}^{\rm op})(h^{-1})\buildrel{\sim}\over{\longrightarrow} {\mathcal{O}}^\sharp_h(h^{-1}). \end{equation}
\begin{equation} ({\mathcal{O}}_h \otimes_{{\mathcal{O}}_{X'}[[h]]} {\mathcal{D}}_{X, [\eta], h}^{\rm op})(h^{-1})\buildrel{\sim}\over{\longrightarrow} {\mathcal{O}}^\sharp_h(h^{-1}). \end{equation}(ii) We have that
(1.9)In particular, if \begin{equation} i^*[{\mathcal{O}}^\sharp_h]= i^*(\delta(\gamma)). \end{equation}
\begin{equation} i^*[{\mathcal{O}}^\sharp_h]= i^*(\delta(\gamma)). \end{equation} $H^2(X, {\mathcal {O}}_X) =0$ then
$H^2(X, {\mathcal {O}}_X) =0$ then  $[{\mathcal {O}}^\sharp _h] = \delta (\gamma )$.
$[{\mathcal {O}}^\sharp _h] = \delta (\gamma )$.
For example, let ![]() $(X, {\mathcal {O}}_h, s)$ be a Frobenius-constant quantization that admits
$(X, {\mathcal {O}}_h, s)$ be a Frobenius-constant quantization that admits ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant structure (1.5). Assume that
${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant structure (1.5). Assume that ![]() $H^2(X, {\mathcal {O}}_X) =0$. Then by Theorem 1
$H^2(X, {\mathcal {O}}_X) =0$. Then by Theorem 1 ![]() ${\mathcal {O}}^\sharp _h$ is a split Azumaya algebra, that is there exists a locally free
${\mathcal {O}}^\sharp _h$ is a split Azumaya algebra, that is there exists a locally free ![]() ${\mathcal {O}}_{X'}[[h]]$-module
${\mathcal {O}}_{X'}[[h]]$-module ![]() $E$ of finite rank and an isomorphism of
$E$ of finite rank and an isomorphism of ![]() ${\mathcal {O}}_{X'}[[h]]$-algebras
${\mathcal {O}}_{X'}[[h]]$-algebras
Using (1.8) and the Azumaya property of ![]() ${\mathcal {O}}_h (h^{-1})$ and
${\mathcal {O}}_h (h^{-1})$ and ![]() ${\mathcal {D}}_{X, [\eta ], h}(h^{-1})$ we observe an equivalence of categories
${\mathcal {D}}_{X, [\eta ], h}(h^{-1})$ we observe an equivalence of categories
between the category of ![]() ${\mathcal {O}}_h (h^{-1})$-modules and the category of
${\mathcal {O}}_h (h^{-1})$-modules and the category of ![]() ${\mathcal {D}}_{X, [\eta ], h}(h^{-1})$-modules. The functor from left to right carries a
${\mathcal {D}}_{X, [\eta ], h}(h^{-1})$-modules. The functor from left to right carries a ![]() ${\mathcal {D}}_{X, [\eta ], h}(h^{-1})$-module
${\mathcal {D}}_{X, [\eta ], h}(h^{-1})$-module ![]() $M$ to
$M$ to ![]() $E\otimes _{{\mathcal {D}}_{X, [\eta ], h}} M$; the quasi-inverse functor takes an
$E\otimes _{{\mathcal {D}}_{X, [\eta ], h}} M$; the quasi-inverse functor takes an ![]() ${\mathcal {O}}_h (h^{-1})$-module
${\mathcal {O}}_h (h^{-1})$-module ![]() $N$ to
$N$ to ![]() ${{\mathcal {H}}}om_{{\mathcal {O}}_h }(E, N)$.
${{\mathcal {H}}}om_{{\mathcal {O}}_h }(E, N)$.
Also note that if ![]() $H^1_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then the map
$H^1_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then the map
is surjective and, thus, any restricted Poisson structure arises from a global ![]() $1$-form
$1$-form ![]() $\eta$. In this case objects of
$\eta$. In this case objects of ![]() $\operatorname {Mod}({\mathcal {D}}_{X, [\eta ], h}(h^{-1}))$ can be viewed as
$\operatorname {Mod}({\mathcal {D}}_{X, [\eta ], h}(h^{-1}))$ can be viewed as ![]() ${\mathcal {D}}_{X, h}(h^{-1})$-modules whose
${\mathcal {D}}_{X, h}(h^{-1})$-modules whose ![]() $p$-curvature equals
$p$-curvature equals ![]() $\eta$.
$\eta$.
1.7  ${\mathbb {G}}_m$-equivariant quantizations
${\mathbb {G}}_m$-equivariant quantizations
Let ![]() $(X, \omega )$ be a symplectic variety equipped with an action
$(X, \omega )$ be a symplectic variety equipped with an action
of the multiplicative group such that ![]() $\omega$ has a positive weight
$\omega$ has a positive weight ![]() $m$ with respect to this action. Moreover, we shall assume that
$m$ with respect to this action. Moreover, we shall assume that ![]() $m$ invertible in
$m$ invertible in ![]() $k$. Denote by
$k$. Denote by ![]() $\theta$ the Euler vector field on
$\theta$ the Euler vector field on ![]() $X$ corresponding to the
$X$ corresponding to the ![]() ${\mathbb {G}}_m$-action. Then the formula
${\mathbb {G}}_m$-action. Then the formula ![]() $\eta = ({1}/{m}) \iota _{\theta } \omega$ defines a restricted structure on
$\eta = ({1}/{m}) \iota _{\theta } \omega$ defines a restricted structure on ![]() $X$. Define a
$X$. Define a ![]() ${\mathbb {G}}_m$-action on
${\mathbb {G}}_m$-action on ![]() $X'$ twisting (1.11) by the
$X'$ twisting (1.11) by the ![]() $p$th power map
$p$th power map ![]() ${\mathbb {G}}_m \stackrel {F}{\longrightarrow } {\mathbb {G}}_m$. Also let
${\mathbb {G}}_m \stackrel {F}{\longrightarrow } {\mathbb {G}}_m$. Also let ![]() ${\mathbb {G}}_m$ act on
${\mathbb {G}}_m$ act on ![]() $X'[h]:= X' \times \operatorname {Spec} k[h]$ as above on the first factor and by
$X'[h]:= X' \times \operatorname {Spec} k[h]$ as above on the first factor and by ![]() $z * h = z^m h$ on the second one.
$z * h = z^m h$ on the second one.
A ![]() ${\mathbb {G}}_m$-equivariant Frobenius-constant quantization of
${\mathbb {G}}_m$-equivariant Frobenius-constant quantization of ![]() $X$ is a
$X$ is a ![]() ${\mathbb {G}}_m$-equivariant sheaf
${\mathbb {G}}_m$-equivariant sheaf ![]() $O_h$ of associative
$O_h$ of associative ![]() ${\mathcal {O}}_{X'[h]}$-algebras on
${\mathcal {O}}_{X'[h]}$-algebras on ![]() $X'[h]$, locally free as an
$X'[h]$, locally free as an ![]() ${\mathcal {O}}_{X'[h]}$-module, such that the restriction
${\mathcal {O}}_{X'[h]}$-module, such that the restriction ![]() ${\mathcal {O}}_h$ of
${\mathcal {O}}_h$ of ![]() $O_h$ to the formal completion of
$O_h$ to the formal completion of ![]() $X'[h]$ along the divisor
$X'[h]$ along the divisor ![]() $h=0$ is a Frobenius-constant quantization of
$h=0$ is a Frobenius-constant quantization of ![]() $X$ compatible with the restricted structure
$X$ compatible with the restricted structure ![]() $[\eta ]$. Examples of
$[\eta ]$. Examples of ![]() ${\mathbb {G}}_m$-equivariant quantizations arise in geometric representation theory (see e.g. [Reference Bezrukavnikov and KaledinBK04b, Reference Bezrukavnikov and FinkelbergBF14, Reference Bezrukavnikov and LosevBL21, Reference Kubrak and TravkinKT19]).
${\mathbb {G}}_m$-equivariant quantizations arise in geometric representation theory (see e.g. [Reference Bezrukavnikov and KaledinBK04b, Reference Bezrukavnikov and FinkelbergBF14, Reference Bezrukavnikov and LosevBL21, Reference Kubrak and TravkinKT19]).
Assume that morphism (1.11) extends to a morphism
Then the restriction of ![]() $O_h$ to the open subscheme
$O_h$ to the open subscheme ![]() $X'[h, h^{-1}]\hookrightarrow X'[h]$ is an Azumaya algebra. As an application of Theorem 1 we prove in § 5 a conjecture of Kubrak and Travkin concerning the class of this algebra in the Brauer group. Namely, we show that, for every
$X'[h, h^{-1}]\hookrightarrow X'[h]$ is an Azumaya algebra. As an application of Theorem 1 we prove in § 5 a conjecture of Kubrak and Travkin concerning the class of this algebra in the Brauer group. Namely, we show that, for every ![]() ${\mathbb {G}}_m$-equivariant Frobenius-constant quantization
${\mathbb {G}}_m$-equivariant Frobenius-constant quantization ![]() $O_h$, the following equality in
$O_h$, the following equality in ![]() $\operatorname {Br}(X')$ holds:
$\operatorname {Br}(X')$ holds:
Here ![]() $[\eta ]$ denotes the image of
$[\eta ]$ denotes the image of ![]() $\eta$ under the canonical map
$\eta$ under the canonical map ![]() $\Gamma (X', \Omega ^1_{X'}) \to \operatorname {Br}(X')$,
$\Gamma (X', \Omega ^1_{X'}) \to \operatorname {Br}(X')$, ![]() $\rho (O_h)\in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$ for the class associated to the formal quantization via (1.4), and
$\rho (O_h)\in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$ for the class associated to the formal quantization via (1.4), and ![]() $[\rho (O_h)]$ for its image in the Brauer group.
$[\rho (O_h)]$ for its image in the Brauer group.
1.8 Plan of the proof
Using the language of formal geometry we reduce the theorem to a group-theoretic statement. We shall start by explaining the latter.
Let ![]() $(V, \omega _V)$ be a finite-dimensional symplectic vector space over
$(V, \omega _V)$ be a finite-dimensional symplectic vector space over ![]() $k$, and let
$k$, and let ![]() $A_h$ be the algebra over
$A_h$ be the algebra over ![]() $k[[h]]$ generated by the dual vector space
$k[[h]]$ generated by the dual vector space ![]() $V^*$ subject to the relations
$V^*$ subject to the relations
for any ![]() $f, g \in V^*$. We refer to
$f, g \in V^*$. We refer to ![]() $A_h$ as the restricted Weyl algebra. This is a flat
$A_h$ as the restricted Weyl algebra. This is a flat ![]() $k[[h]]$-algebra whose reduction modulo
$k[[h]]$-algebra whose reduction modulo ![]() $h$ is the finite-dimensional commutative algebra of functions on the Frobenius neighborhood of the origin in the affine space
$h$ is the finite-dimensional commutative algebra of functions on the Frobenius neighborhood of the origin in the affine space ![]() $\operatorname {Spec}(S^{\cdot } V^*) := \bf {V}$. Explicitly,
$\operatorname {Spec}(S^{\cdot } V^*) := \bf {V}$. Explicitly, ![]() $A_0 := S^{\cdot } V^* / J_V$ where
$A_0 := S^{\cdot } V^* / J_V$ where ![]() $J_V$ is the ideal generated by
$J_V$ is the ideal generated by ![]() $f^p$ for all
$f^p$ for all ![]() $f \in V^*$. The quantization
$f \in V^*$. The quantization ![]() $A_h$ of
$A_h$ of ![]() $A_0$ specifies a restricted Poisson structure
$A_0$ specifies a restricted Poisson structure ![]() $[\eta _V]\in \operatorname {coker}(A_0 \stackrel {d}{\longrightarrow } \Omega ^1_{A_0})$.Footnote 4
$[\eta _V]\in \operatorname {coker}(A_0 \stackrel {d}{\longrightarrow } \Omega ^1_{A_0})$.Footnote 4
Denote by ![]() $G$ the group scheme
$G$ the group scheme ![]() $\underline {\operatorname {Aut}}(A_h)$ of
$\underline {\operatorname {Aut}}(A_h)$ of ![]() $k[[h]]$-linear automorphisms of the algebra
$k[[h]]$-linear automorphisms of the algebra ![]() $A_h$, by
$A_h$, by ![]() $G^{\geq 1}$ the subgroup of automorphisms identical modulo
$G^{\geq 1}$ the subgroup of automorphisms identical modulo ![]() $h$, and by
$h$, and by ![]() $G_0$ the quotient of
$G_0$ the quotient of ![]() $G$ by
$G$ by ![]() $G^{\geq 1}$. As shown in [Reference Bezrukavnikov and KaledinBK08],
$G^{\geq 1}$. As shown in [Reference Bezrukavnikov and KaledinBK08], ![]() $G_0$ is the group scheme of automorphisms of
$G_0$ is the group scheme of automorphisms of ![]() $A_0$ preserving the class
$A_0$ preserving the class ![]() $[\eta _V]$.
$[\eta _V]$.
A pair ![]() $(W, W^*)$ of transversal Lagrangian subspaces of
$(W, W^*)$ of transversal Lagrangian subspaces of ![]() $V$ defines an isomorphism between the algebra
$V$ defines an isomorphism between the algebra ![]() $A_h(h^{-1})$ and the matrix algebra
$A_h(h^{-1})$ and the matrix algebra ![]() $\operatorname {End}_{k}(S^{\cdot } W^* / J_W)((h))$ which, in turn, gives an embedding
$\operatorname {End}_{k}(S^{\cdot } W^* / J_W)((h))$ which, in turn, gives an embedding ![]() $G \hookrightarrow L\operatorname {PGL}(p^n)$, where
$G \hookrightarrow L\operatorname {PGL}(p^n)$, where ![]() $L\operatorname {PGL}(p^n)$ is the loop group of
$L\operatorname {PGL}(p^n)$ is the loop group of ![]() $\operatorname {PGL}(p^n)$ (viewed as a sheaf for the fpqc topology). Then the extension
$\operatorname {PGL}(p^n)$ (viewed as a sheaf for the fpqc topology). Then the extension
gives rise toFootnote 5
In [Reference Bezrukavnikov and KaledinBK08] it is proved that ![]() $G^{\geq 1}$ is the subgroup of inner automorphisms. Hence, we have a subextension of (1.13)
$G^{\geq 1}$ is the subgroup of inner automorphisms. Hence, we have a subextension of (1.13)
where ![]() $L^+{\mathbb {G}}_m$ is the positive loop group of
$L^+{\mathbb {G}}_m$ is the positive loop group of ![]() $\mathbb {G}_m$. Then passing to the quotient we get a central extension by the affine grassmannianFootnote 6
$\mathbb {G}_m$. Then passing to the quotient we get a central extension by the affine grassmannianFootnote 6
Let ![]() $i: V\hookrightarrow V^{\flat }$ be a morphism of symplectic vector spaces such that the restriction to
$i: V\hookrightarrow V^{\flat }$ be a morphism of symplectic vector spaces such that the restriction to ![]() $V$ of the symplectic form on
$V$ of the symplectic form on ![]() $V^{\flat }$ is
$V^{\flat }$ is ![]() $\omega _V$. Let
$\omega _V$. Let ![]() $\widetilde {G}_0 \to G_0$ and
$\widetilde {G}_0 \to G_0$ and ![]() $\widetilde {G}_0^{\flat } \to G_0^{\flat }$ be the corresponding extensions. We emphasize that
$\widetilde {G}_0^{\flat } \to G_0^{\flat }$ be the corresponding extensions. We emphasize that ![]() $\widetilde {G}_0$ and
$\widetilde {G}_0$ and ![]() $\widetilde {G}_0^{\flat }$ depend on a choice of Lagrangian pairs in
$\widetilde {G}_0^{\flat }$ depend on a choice of Lagrangian pairs in ![]() $V$ and
$V$ and ![]() $V^{\flat }$.
$V^{\flat }$.
Finally, denote by ![]() $G_0^{\sharp }\subset G_0^\flat$ the group subscheme that consists of automorphisms preserving the kernel of the homomorphism
$G_0^{\sharp }\subset G_0^\flat$ the group subscheme that consists of automorphisms preserving the kernel of the homomorphism ![]() $i^*: A_0^{\flat } \to A_0$. We have a natural homomorphism
$i^*: A_0^{\flat } \to A_0$. We have a natural homomorphism ![]() $G_0^{\sharp } \to G_0$. In § 4 we prove the following assertion.
$G_0^{\sharp } \to G_0$. In § 4 we prove the following assertion.
Theorem 1 The homomorphism ![]() $G_0^{\sharp } \to G_0$ lifts uniquely to a homomorphism of central extensions
$G_0^{\sharp } \to G_0$ lifts uniquely to a homomorphism of central extensions
Our proof of the Basic Lemma, that occupies almost the half of the paper, is based on a new construction of (1.15) that makes this functoriality property obvious. Namely, consider two subgroups ![]() $\alpha \subset G_0 \supset G_0^0$, where
$\alpha \subset G_0 \supset G_0^0$, where ![]() $G_0^0$ is the subgroup of automorphisms preserving the origin in
$G_0^0$ is the subgroup of automorphisms preserving the origin in ![]() $\bf {V}$ (which by a result of Bezrukavnikov and Kaledin coincides with the reduced subgroup of
$\bf {V}$ (which by a result of Bezrukavnikov and Kaledin coincides with the reduced subgroup of ![]() $G_0$) and
$G_0$) and ![]() $\alpha =\operatorname {Spec} A_0 (\cong \alpha _p^{\dim V})$ is the finite group scheme of translations. Then the product map
$\alpha =\operatorname {Spec} A_0 (\cong \alpha _p^{\dim V})$ is the finite group scheme of translations. Then the product map ![]() $\alpha \times G_0^0 \to G_0$ induces an isomorphism of the underlying schemes. Let
$\alpha \times G_0^0 \to G_0$ induces an isomorphism of the underlying schemes. Let ![]() $\widetilde {\alpha }$ be the restriction of the central extension (1.15) to
$\widetilde {\alpha }$ be the restriction of the central extension (1.15) to ![]() $\alpha$. This is a version of the Heisenberg group. We show that the extension (1.15) splits uniquely over the reduced subgroup
$\alpha$. This is a version of the Heisenberg group. We show that the extension (1.15) splits uniquely over the reduced subgroup ![]() $G_0^0$.Footnote 7 Thus, we can view
$G_0^0$.Footnote 7 Thus, we can view ![]() $G_0^0$ as a subgroup of
$G_0^0$ as a subgroup of ![]() $\widetilde {G_0}$, and the quotient
$\widetilde {G_0}$, and the quotient ![]() $\widetilde {G_0}/G_0^0$ is identified (as an ind-scheme) with
$\widetilde {G_0}/G_0^0$ is identified (as an ind-scheme) with ![]() $\widetilde {\alpha }$. The left action of
$\widetilde {\alpha }$. The left action of ![]() $\widetilde {G_0}$ on
$\widetilde {G_0}$ on ![]() $\widetilde {G_0}/G_0^0$ defines an embedding of
$\widetilde {G_0}/G_0^0$ defines an embedding of ![]() $\widetilde {G_0}$ into the group of automorphisms of
$\widetilde {G_0}$ into the group of automorphisms of ![]() $\widetilde {\alpha }$ viewed as a space with an action of
$\widetilde {\alpha }$ viewed as a space with an action of ![]() $\operatorname {Gr}_{{\mathbb {G}}_m}$. We prove in Theorem 3 that the image of this embedding is precisely the group of automorphisms that preserve a unique
$\operatorname {Gr}_{{\mathbb {G}}_m}$. We prove in Theorem 3 that the image of this embedding is precisely the group of automorphisms that preserve a unique ![]() $\operatorname {Sp}_{2 n} \ltimes \alpha _{p}^{2 n}$-invariant connection on
$\operatorname {Sp}_{2 n} \ltimes \alpha _{p}^{2 n}$-invariant connection on ![]() $\operatorname {Gr}_{{\mathbb {G}}_m}$-torsor
$\operatorname {Gr}_{{\mathbb {G}}_m}$-torsor ![]() $\widetilde {\alpha }$.
$\widetilde {\alpha }$.
To derive the Basic Lemma from the above, we classify all central extensions of ![]() $\alpha$ by
$\alpha$ by ![]() $\operatorname {Gr}_{\mathbb {G}_m}$ in § 4.2. In particular, we show that extensions of
$\operatorname {Gr}_{\mathbb {G}_m}$ in § 4.2. In particular, we show that extensions of ![]() $\alpha$ by
$\alpha$ by ![]() $\operatorname {Gr}_{\mathbb {G}_m}$ that split over every
$\operatorname {Gr}_{\mathbb {G}_m}$ that split over every ![]() $\alpha _{p}$ factor are classified by
$\alpha _{p}$ factor are classified by ![]() $\operatorname {Lie}(\operatorname {Gr}_{\mathbb {G}_m})$-valued skew-symmetric
$\operatorname {Lie}(\operatorname {Gr}_{\mathbb {G}_m})$-valued skew-symmetric ![]() $2$-forms on
$2$-forms on ![]() $\operatorname {Lie}(\alpha )$. Then it follows that the morphism
$\operatorname {Lie}(\alpha )$. Then it follows that the morphism ![]() $\alpha \rightarrow \alpha ^{\flat }$ induced by
$\alpha \rightarrow \alpha ^{\flat }$ induced by ![]() $i$ lifts uniquely to a morphism of extensions
$i$ lifts uniquely to a morphism of extensions ![]() $\widetilde {\alpha } \rightarrow \widetilde {\alpha }^{\flat }$ respecting the connections. Since
$\widetilde {\alpha } \rightarrow \widetilde {\alpha }^{\flat }$ respecting the connections. Since ![]() $\widetilde G_0^\flat \times _{G_0^\flat } G_0^{\sharp }$ is the group of automorphisms of
$\widetilde G_0^\flat \times _{G_0^\flat } G_0^{\sharp }$ is the group of automorphisms of ![]() $\widetilde {\alpha }^{\flat }$ that preserve the connection and the subspace
$\widetilde {\alpha }^{\flat }$ that preserve the connection and the subspace ![]() $\widetilde {\alpha } \hookrightarrow \widetilde {\alpha }^{\flat }$, by restriction we get the desired lifting
$\widetilde {\alpha } \hookrightarrow \widetilde {\alpha }^{\flat }$, by restriction we get the desired lifting ![]() $\widetilde {G}_0^\flat \times _{G_0^\flat } G_0^{\sharp } \to \tilde {G}_0.$
$\widetilde {G}_0^\flat \times _{G_0^\flat } G_0^{\sharp } \to \tilde {G}_0.$
Let us explain how the Basic Lemma implies the theorem. The Bezrukavnikov–Kaledin construction of Frobenius-constant quantizations is based on a characteristic-![]() $p$ version of the Gelfand–Kazhdan formal geometry. Namely, it is shown in [Reference Bezrukavnikov and KaledinBK04b] that any Frobenius-constant quantization is locally for the fpqc topology on
$p$ version of the Gelfand–Kazhdan formal geometry. Namely, it is shown in [Reference Bezrukavnikov and KaledinBK04b] that any Frobenius-constant quantization is locally for the fpqc topology on ![]() $X^{\prime }$ isomorphic to the constant quantization
$X^{\prime }$ isomorphic to the constant quantization ![]() $\mathcal {O}_{X^{\prime }}[[h]] \otimes _{k[[h]]} A_h$ for a fixed finite-dimensional space
$\mathcal {O}_{X^{\prime }}[[h]] \otimes _{k[[h]]} A_h$ for a fixed finite-dimensional space ![]() $V$ of dimension
$V$ of dimension ![]() $2n = \dim X$. It follows that a Frobenius-constant quantization
$2n = \dim X$. It follows that a Frobenius-constant quantization ![]() $(X, \mathcal {O}_h, s)$ gives rise to a torsor
$(X, \mathcal {O}_h, s)$ gives rise to a torsor ![]() $\mathcal {M}_{X, \mathcal {O}_h, s}$ over
$\mathcal {M}_{X, \mathcal {O}_h, s}$ over ![]() $G$. Conversely, the algebra
$G$. Conversely, the algebra ![]() $\mathcal {O}_h$ is the twist of
$\mathcal {O}_h$ is the twist of ![]() $\mathcal {O}_{X^{\prime }}[[h]] \otimes _{k[[h]]} A_h$ by the torsor
$\mathcal {O}_{X^{\prime }}[[h]] \otimes _{k[[h]]} A_h$ by the torsor ![]() ${\mathcal {M}}_{X, \mathcal {O}_h, s}$, i.e.
${\mathcal {M}}_{X, \mathcal {O}_h, s}$, i.e.
The reduction of differential operators ![]() ${\mathcal {D}}_{X, [\eta ], h}$ also can be constructed using formal geometry. Namely, choosing a homogeneous form
${\mathcal {D}}_{X, [\eta ], h}$ also can be constructed using formal geometry. Namely, choosing a homogeneous form ![]() $\eta _V$ in the class
$\eta _V$ in the class ![]() $[\eta _V]$ on
$[\eta _V]$ on ![]() $V$ consider its graph
$V$ consider its graph
and let ![]() $i : V \to V\oplus V^*= V^{\flat }$ be the corresponding linear map of vector spaces. Let
$i : V \to V\oplus V^*= V^{\flat }$ be the corresponding linear map of vector spaces. Let ![]() $G_0^{\sharp, f}$ be the subgroup of
$G_0^{\sharp, f}$ be the subgroup of ![]() $G_0^{\sharp } \subset G_0^{\flat }$ of automorphisms
$G_0^{\sharp } \subset G_0^{\flat }$ of automorphisms ![]() $g$ of
$g$ of ![]() $\alpha ^{\flat }$ respecting the fibers of the projection
$\alpha ^{\flat }$ respecting the fibers of the projection ![]() $\pi : \alpha ^{\flat } \to \alpha$, that is fitting in the following diagram.
$\pi : \alpha ^{\flat } \to \alpha$, that is fitting in the following diagram.

Then the restriction of the natural map ![]() $G_0^{\sharp } \to G_0$ to
$G_0^{\sharp } \to G_0$ to ![]() $G_0^{\sharp, f}$ is an isomorphism. This yields a homomorphism
$G_0^{\sharp, f}$ is an isomorphism. This yields a homomorphism ![]() $\psi _0 : G_0 \hookrightarrow G_0^{\sharp } \subset G_0^{\flat }$. In § 3.1 we construct a lifting
$\psi _0 : G_0 \hookrightarrow G_0^{\sharp } \subset G_0^{\flat }$. In § 3.1 we construct a lifting ![]() $\psi : G \to G^{\flat }$ of
$\psi : G \to G^{\flat }$ of ![]() $\psi _0$ that makes
$\psi _0$ that makes ![]() $\mathcal {D}_{X, [\eta ], h}$ a twist of
$\mathcal {D}_{X, [\eta ], h}$ a twist of ![]() $\mathcal {O}_{X^{\prime }}[[h]] \otimes _{k[[h]]} A_h^{\flat }$ by
$\mathcal {O}_{X^{\prime }}[[h]] \otimes _{k[[h]]} A_h^{\flat }$ by ![]() ${\mathcal {M}}_{X, \mathcal {O}_h, s}$.
${\mathcal {M}}_{X, \mathcal {O}_h, s}$.
Then we consider the following diagram.

Here the loop group ![]() $L\operatorname {PGL}$ is the group ind-scheme of projective automorphisms of a certain vector space
$L\operatorname {PGL}$ is the group ind-scheme of projective automorphisms of a certain vector space ![]() $U$ over
$U$ over ![]() $k((h))$. Suppose we can construct a
$k((h))$. Suppose we can construct a ![]() $G$-invariant
$G$-invariant ![]() $k[[h]]$-lattice
$k[[h]]$-lattice ![]() $\Lambda$ in
$\Lambda$ in ![]() $U$. Then
$U$. Then
does the job for the first part of the theorem. By a general result proven in the Appendix (Proposition A.5) the existence of an invariant lattice is equivalent to the existence of the dashed arrow making the diagram above commutative. This is where we use the Basic Lemma. It follows from the latter that
We infer (Proposition 3.3) that ![]() $\psi _0$ lifts to
$\psi _0$ lifts to ![]() $\widetilde {\psi }_0 : \widetilde {G}_0 \to \widetilde {G}_0^{\flat }$, which implies the existence of the dashed arrow.
$\widetilde {\psi }_0 : \widetilde {G}_0 \to \widetilde {G}_0^{\flat }$, which implies the existence of the dashed arrow.
The proof of the second part of the theorem amounts to unveiling the Bezrukavnikov–Kaledin construction of the map ![]() $\rho$.
$\rho$.
1.9 Further directions
In this subsection we briefly discuss some applications of Theorem 1 obtained in a sequel paper joint with Dmitry Kubrak and Roman Travkin [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22].
According to the Bezrukavnikov–Kaledin theorem from § 1.4 every smooth affine restricted symplectic variety admits a unique up to a non-canonical isomorphism Frobenius-constant quantization ![]() $O_h$ with
$O_h$ with ![]() $\rho [O_h]=0$. The formation of
$\rho [O_h]=0$. The formation of ![]() $O_h$ is not functorial in
$O_h$ is not functorial in ![]() $(X, [\eta ])$. However, we show in [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22] that the assignment
$(X, [\eta ])$. However, we show in [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22] that the assignment ![]() $(X, [\eta ]) \mapsto \operatorname {Mod}(O_h(X))$ extends to a contravariant functor from the category of smooth affine restricted symplectic varieties and open embeddings to the category of abelian categories. Applying the right Kan extension this yields a functorial quantization
$(X, [\eta ]) \mapsto \operatorname {Mod}(O_h(X))$ extends to a contravariant functor from the category of smooth affine restricted symplectic varieties and open embeddings to the category of abelian categories. Applying the right Kan extension this yields a functorial quantization ![]() $\operatorname {QCoh}_h$ of the category of quasi-coherent sheaves of any smooth restricted symplectic variety. Moreover, using Remark 1.1 and equivalence (1.10) we extend the range of quantum parameter
$\operatorname {QCoh}_h$ of the category of quasi-coherent sheaves of any smooth restricted symplectic variety. Moreover, using Remark 1.1 and equivalence (1.10) we extend the range of quantum parameter ![]() $h$ from being a formal variable to a genuine coordinate on
$h$ from being a formal variable to a genuine coordinate on ![]() ${\mathbb {P}}^1$. The construction of
${\mathbb {P}}^1$. The construction of ![]() $\operatorname {QCoh}_h$ uses in an essential way Corollary 3.5 of the Basic Lemma.
$\operatorname {QCoh}_h$ uses in an essential way Corollary 3.5 of the Basic Lemma.
Let ![]() $Y\hookrightarrow X$ be a smooth Lagrangian subvariety such that
$Y\hookrightarrow X$ be a smooth Lagrangian subvariety such that ![]() $[\eta ]_{|Y} = 0$ in
$[\eta ]_{|Y} = 0$ in ![]() $H_{\rm Zar}^{0}\big (Y, \Omega _{Y}^{1}/d{\mathcal {O}}_Y\big )$. Using results from [Reference MundingerMun22] we show in § 6.1 of [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22] that every such
$H_{\rm Zar}^{0}\big (Y, \Omega _{Y}^{1}/d{\mathcal {O}}_Y\big )$. Using results from [Reference MundingerMun22] we show in § 6.1 of [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22] that every such ![]() $Y$ determines a canonical object in
$Y$ determines a canonical object in ![]() $\operatorname {QCoh}_h$, which is a quantization of the line bundle
$\operatorname {QCoh}_h$, which is a quantization of the line bundle ![]() $(\Omega _{Y}^n)^{ ({1-p})/{2}}$ viewed as a quasi-coherent sheaf on
$(\Omega _{Y}^n)^{ ({1-p})/{2}}$ viewed as a quasi-coherent sheaf on ![]() $X$.
$X$.
1.10 Plan of the paper
In § 2 we review the Bezrukavnikov–Kaledin construction of Frobenius-constant quantizations which is based on a characteristic ![]() $p$ version of the Gelfand–Kazhdan formal geometry. In § 3 we recast the construction of
$p$ version of the Gelfand–Kazhdan formal geometry. In § 3 we recast the construction of ![]() ${\mathcal {D}}_{X, h}$ using the language of formal geometry and reduce Theorem 1 to a certain statement on central extensions of the group of automorphisms of the restricted Weyl algebra. In § 4 we prove this statement. In § 5 we study
${\mathcal {D}}_{X, h}$ using the language of formal geometry and reduce Theorem 1 to a certain statement on central extensions of the group of automorphisms of the restricted Weyl algebra. In § 4 we prove this statement. In § 5 we study ![]() $\mathbb {G}_m$-equivariant quantizations and prove a conjecture of Kubrak and Travkin. Finally, in the Appendix we prove some results (probably known to experts) on loop groups that are used in the main body of the paper.
$\mathbb {G}_m$-equivariant quantizations and prove a conjecture of Kubrak and Travkin. Finally, in the Appendix we prove some results (probably known to experts) on loop groups that are used in the main body of the paper.
2. Review of the Bezrukavnikov–Kaledin construction
For reader's convenience we review the Bezrukavnikov–Kaledin construction of quantizations. We also introduce some notation to be used later. Nothing in this section is an invention of the authors.
2.1 Darboux lemma in characteristic  $p$
$p$
Our proof of Theorem 1, as well as the Bezrukavnikov–Kaledin construction of quantizations, is based on a version of the Gelfand–Kazhdan formal geometry that makes it possible to localize the problem and ultimately reduce it to a statement in group theory. The main idea is as follows. For a symplectic variety ![]() $X$, the Poisson bracket on
$X$, the Poisson bracket on ![]() ${\mathcal {O}}_X$ is
${\mathcal {O}}_X$ is ![]() ${\mathcal {O}}_{X'}$-linear. Therefore, we can view
${\mathcal {O}}_{X'}$-linear. Therefore, we can view ![]() $X$ as a Poisson scheme over
$X$ as a Poisson scheme over ![]() $X'$. For any restricted structure on
$X'$. For any restricted structure on ![]() ${\mathcal {O}}_X$, one has
${\mathcal {O}}_X$, one has ![]() ${\mathcal {O}}_{X'}^{[p]}=0$. Therefore, a symplectic variety
${\mathcal {O}}_{X'}^{[p]}=0$. Therefore, a symplectic variety ![]() $X$ with a restricted structure can be viewed as a restricted Poisson scheme over
$X$ with a restricted structure can be viewed as a restricted Poisson scheme over ![]() $X'$. Consider the constant restricted Poisson scheme over
$X'$. Consider the constant restricted Poisson scheme over ![]() $X'$:
$X'$:
where
![]() $2n=\dim X$, the morphism (2.1) is the projection to the first factor, the Poisson structure is given by symplectic form
$2n=\dim X$, the morphism (2.1) is the projection to the first factor, the Poisson structure is given by symplectic form ![]() $\sum _i dy_i\wedge dx_i$, and the restricted structure is determined by
$\sum _i dy_i\wedge dx_i$, and the restricted structure is determined by ![]() $x_i^{[p]} = y_i^{[p]}=0$. A key insight of Bezrukavnikov and Kaledin is that any smooth symplectic variety
$x_i^{[p]} = y_i^{[p]}=0$. A key insight of Bezrukavnikov and Kaledin is that any smooth symplectic variety ![]() $X$ with a restricted structure, viewed as a restricted Poisson scheme over
$X$ with a restricted structure, viewed as a restricted Poisson scheme over ![]() $X'$, is locally for the fpqc topology on
$X'$, is locally for the fpqc topology on ![]() $X'$ isomorphic to the constant restricted Poisson scheme
$X'$ isomorphic to the constant restricted Poisson scheme ![]() $X' \times \operatorname {Spec} A_0 \to X'$. This is an analogue of the Darboux lemma.
$X' \times \operatorname {Spec} A_0 \to X'$. This is an analogue of the Darboux lemma.
2.2 Quantum Darboux lemma
There is also a quantum version of the Darboux lemma proven in [Reference Bezrukavnikov and KaledinBK08]: for any Frobenius-constant quantization ![]() $(X, {\mathcal {O}}_h, s)$, the sheaf of associative
$(X, {\mathcal {O}}_h, s)$, the sheaf of associative ![]() ${\mathcal {O}}_{X'}[[h]]$-algebras
${\mathcal {O}}_{X'}[[h]]$-algebras ![]() ${\mathcal {O}}_h$ is isomorphic locally for the fpqc topology on
${\mathcal {O}}_h$ is isomorphic locally for the fpqc topology on ![]() $X'$ to the
$X'$ to the ![]() $h$-completed tensor product
$h$-completed tensor product ![]() ${\mathcal {O}}_{X'}\otimes _k A_h$, where
${\mathcal {O}}_{X'}\otimes _k A_h$, where ![]() $A_h$ is the reduced Weyl algebra that is the
$A_h$ is the reduced Weyl algebra that is the ![]() $k[[h]]$-algebra generated by variable
$k[[h]]$-algebra generated by variable ![]() $x_i, y_i$
$x_i, y_i$ ![]() $(1\leq i,j, \leq n)$, subject to the relations
$(1\leq i,j, \leq n)$, subject to the relations
2.3 Formal geometry
Let ![]() $\underline {\operatorname {Aut}}(A_0)$ be the group scheme of automorphisms of the algebra
$\underline {\operatorname {Aut}}(A_0)$ be the group scheme of automorphisms of the algebra ![]() $A_0$. For any smooth scheme
$A_0$. For any smooth scheme ![]() $X$ over
$X$ over ![]() $k$ of dimension
$k$ of dimension ![]() $2n$, assigning to a scheme
$2n$, assigning to a scheme ![]() $Z$ over
$Z$ over ![]() $X'$ the set
$X'$ the set ![]() ${\mathcal {M}}_X(Z)$ of isomorphisms
${\mathcal {M}}_X(Z)$ of isomorphisms
of schemes over ![]() $Z$, we get a
$Z$, we get a ![]() $\underline {\operatorname {Aut}}(A_0)$-torsor over
$\underline {\operatorname {Aut}}(A_0)$-torsor over ![]() $X'$. Next, let
$X'$. Next, let ![]() $G_0\subset \underline {\operatorname {Aut}}(A_0)$ be the group subscheme consisting of automorphisms of
$G_0\subset \underline {\operatorname {Aut}}(A_0)$ be the group subscheme consisting of automorphisms of ![]() $A_0$ that preserve the restricted Poisson structure on
$A_0$ that preserve the restricted Poisson structure on ![]() $A_0$. Then the Darboux lemma above implies that, for every symplectic variety
$A_0$. Then the Darboux lemma above implies that, for every symplectic variety ![]() $(X, [\eta ])$ with a restricted structure of dimension
$(X, [\eta ])$ with a restricted structure of dimension ![]() $2n$ the functor assigning to a scheme
$2n$ the functor assigning to a scheme ![]() $Z$ over
$Z$ over ![]() $X'$ the set
$X'$ the set ![]() ${\mathcal {M}}_{X, [\eta ]}(Z)$ of isomorphisms
${\mathcal {M}}_{X, [\eta ]}(Z)$ of isomorphisms
of restricted Poisson schemes over ![]() $Z$ is a
$Z$ is a ![]() $G_0$-torsor over
$G_0$-torsor over ![]() $X'$. Using the faithfully flat descent one gets a bijection between the set of nondegenerate (that is, arising from a symplectic form) restricted Poisson structures
$X'$. Using the faithfully flat descent one gets a bijection between the set of nondegenerate (that is, arising from a symplectic form) restricted Poisson structures ![]() $[\eta ]$ on
$[\eta ]$ on ![]() $X$ and the set of
$X$ and the set of ![]() $G_0$-torsors over
$G_0$-torsors over ![]() $X'$ equipped with an isomorphism of
$X'$ equipped with an isomorphism of ![]() $\operatorname {Aut}(A_0)$-torsors
$\operatorname {Aut}(A_0)$-torsors
Lastly, the set of all Frobenius-constant quantizations ![]() $(X, {\mathcal {O}}_h, s)$ of
$(X, {\mathcal {O}}_h, s)$ of ![]() $X$ such that the induced Poisson structure on
$X$ such that the induced Poisson structure on ![]() $X$ is nondegenerate is in bijection with the set of torsors
$X$ is nondegenerate is in bijection with the set of torsors ![]() ${\mathcal {M}}_{X, {\mathcal {O}}_h, s}$ over the group scheme
${\mathcal {M}}_{X, {\mathcal {O}}_h, s}$ over the group scheme ![]() $G: = \underline {\operatorname {Aut}}(A_h)$ of automorphisms of
$G: = \underline {\operatorname {Aut}}(A_h)$ of automorphisms of ![]() $k[[h]]$-algebra
$k[[h]]$-algebra ![]() $A_h$ (that is a group scheme whose group of points with values in a
$A_h$ (that is a group scheme whose group of points with values in a ![]() $k$-algebra
$k$-algebra ![]() $R$ is the group of
$R$ is the group of ![]() $R[[h]]$-algebra automorphisms of the
$R[[h]]$-algebra automorphisms of the ![]() $h$-adically completed tensor product
$h$-adically completed tensor product ![]() $A_h \hat {\otimes } R$) together with an isomorphism
$A_h \hat {\otimes } R$) together with an isomorphism ![]() $\underline {\operatorname {Aut}}(A_0)$-torsors
$\underline {\operatorname {Aut}}(A_0)$-torsors
In particular, for a symplectic variety with a restricted structure ![]() $(X, [\eta ])$, giving a Frobenius constant quantization of
$(X, [\eta ])$, giving a Frobenius constant quantization of ![]() $(X, [\eta ])$ is equivalent to lifting a
$(X, [\eta ])$ is equivalent to lifting a ![]() $G_0$-torsor
$G_0$-torsor ![]() ${\mathcal {M}}_{X, [\eta ]}$ to a
${\mathcal {M}}_{X, [\eta ]}$ to a ![]() $G$-torsor
$G$-torsor ![]() ${\mathcal {M}}_{X, {\mathcal {O}}_h, s}$ along the group scheme homomorphism
${\mathcal {M}}_{X, {\mathcal {O}}_h, s}$ along the group scheme homomorphism
2.4 Automorphisms of the reduced Weyl algebra
It was shown in [Reference Bezrukavnikov and KaledinBK08] that homomorphism (2.4) is surjective and its kernel ![]() $G^{\geq 1}$ consists of inner automorphisms. We have the exact sequence
$G^{\geq 1}$ consists of inner automorphisms. We have the exact sequence
Here ![]() $\underline A_h ^*$ (respectively,
$\underline A_h ^*$ (respectively, ![]() $L^+{\mathbb {G}}_m$) is the group scheme over
$L^+{\mathbb {G}}_m$) is the group scheme over ![]() $k$ whose group of
$k$ whose group of ![]() $R$-points is
$R$-points is ![]() $(R\otimes A_h)^*$ (respectively,
$(R\otimes A_h)^*$ (respectively, ![]() $R[[h]]^*$). Letting
$R[[h]]^*$). Letting ![]() $G^{\geq n} \subset G$ (
$G^{\geq n} \subset G$ (![]() $n\geq 0$), be the group subscheme consisting of automorphisms that are identical modulo
$n\geq 0$), be the group subscheme consisting of automorphisms that are identical modulo ![]() $h^{n}$, we have that
$h^{n}$, we have that ![]() $G^{\geq n}/G^{\geq n+1}\buildrel {\sim }\over {\longrightarrow } \underline {A}_0/{\mathbb {G}}_a$ for every
$G^{\geq n}/G^{\geq n+1}\buildrel {\sim }\over {\longrightarrow } \underline {A}_0/{\mathbb {G}}_a$ for every ![]() $n>1$ and
$n>1$ and ![]() $G^{\geq 1}/G^{\geq 2}\buildrel {\sim }\over {\longrightarrow } \underline {A}_0^*/{\mathbb {G}}_m$,
$G^{\geq 1}/G^{\geq 2}\buildrel {\sim }\over {\longrightarrow } \underline {A}_0^*/{\mathbb {G}}_m$, ![]() $G^{\geq 0}/G^{\geq 1}\buildrel {\sim }\over {\longrightarrow } G_0$.
$G^{\geq 0}/G^{\geq 1}\buildrel {\sim }\over {\longrightarrow } G_0$.
Consider the isomorphism of ![]() $k[[h]]$-algebras
$k[[h]]$-algebras
sending ![]() $x_i$ to
$x_i$ to ![]() $x_i$ and
$x_i$ and ![]() $y_j$ to
$y_j$ to ![]() $y_j$. The conjugation by
$y_j$. The conjugation by ![]() $\alpha$ defines an involution
$\alpha$ defines an involution ![]() $\tau : G\to G$ preserving the subgroups
$\tau : G\to G$ preserving the subgroups ![]() $G^{\geq n}$, (
$G^{\geq n}$, (![]() $n\geq 0$), such that the induced action on
$n\geq 0$), such that the induced action on ![]() $G^{\geq n}/G^{\geq n+1}$ takes an element
$G^{\geq n}/G^{\geq n+1}$ takes an element ![]() $g$ to
$g$ to ![]() $g^{(-1)^n}$. In particular, it follows that the extension
$g^{(-1)^n}$. In particular, it follows that the extension
has a unique ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant splitting
${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant splitting
2.5  ${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant structures
${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant structures
Any ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant Frobenius-constant quantization
${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant Frobenius-constant quantization ![]() $(X, {\mathcal {O}}_h, s, \alpha )$ is isomorphic locally for the fpqc topology on
$(X, {\mathcal {O}}_h, s, \alpha )$ is isomorphic locally for the fpqc topology on ![]() $X'$ to the
$X'$ to the ![]() $h$-completed tensor product
$h$-completed tensor product ![]() ${\mathcal {O}}_{X'}\hat \otimes _k A_h$ equipped with the equivariant structure (2.6). Indeed, consider the action of
${\mathcal {O}}_{X'}\hat \otimes _k A_h$ equipped with the equivariant structure (2.6). Indeed, consider the action of ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$ on
${\mathbb {Z}}/2{\mathbb {Z}}$ on ![]() $G^{\geq 1}$ given by
$G^{\geq 1}$ given by ![]() $\tau$. Then
$\tau$. Then ![]() ${H^1({\mathbb {Z}}/2{\mathbb {Z}}, G^{\geq 1})=0}$ as
${H^1({\mathbb {Z}}/2{\mathbb {Z}}, G^{\geq 1})=0}$ as ![]() $G^{\geq 1}$ has a filtration
$G^{\geq 1}$ has a filtration ![]() $G^{\geq n}$ with uniquely
$G^{\geq n}$ with uniquely ![]() $2$-divisible quotients. It follows that every two
$2$-divisible quotients. It follows that every two ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant structures on
${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant structures on ![]() ${\mathcal {O}}_{X'}\hat \otimes _k A_h$ are locally isomorphic. Now the claim follows from the quantum Darboux lemma.
${\mathcal {O}}_{X'}\hat \otimes _k A_h$ are locally isomorphic. Now the claim follows from the quantum Darboux lemma.
Consequently, giving a ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant Frobenius constant quantization of
${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant Frobenius constant quantization of ![]() $(X, [\eta ])$ is equivalent to lifting a
$(X, [\eta ])$ is equivalent to lifting a ![]() $G_0$-torsor
$G_0$-torsor ![]() ${\mathcal {M}}_{X, [\eta ]}$ to a torsor
${\mathcal {M}}_{X, [\eta ]}$ to a torsor ![]() ${\mathcal {M}}_{X, {\mathcal {O}}_h, s, \alpha }$ over the subgroup
${\mathcal {M}}_{X, {\mathcal {O}}_h, s, \alpha }$ over the subgroup ![]() $G^{\tau =1} \subset G$ of
$G^{\tau =1} \subset G$ of ![]() $\tau$-invariants.
$\tau$-invariants.
2.6 Construction of quantizations
Bezrukavnikov and Kaledin use the standard obstruction theory to classify liftings of a given ![]() $G_0$-torsor to a
$G_0$-torsor to a ![]() $G$-torsor. Namely, given a
$G$-torsor. Namely, given a ![]() $G_0$-torsor
$G_0$-torsor ![]() ${\mathcal {M}}_{X, [\eta ]}$ the set of isomorphism classes of its liftings to a torsor over
${\mathcal {M}}_{X, [\eta ]}$ the set of isomorphism classes of its liftings to a torsor over ![]() $G/G^{\geq 2}\buildrel {\sim }\over {\longrightarrow } G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$ is identified with the set of isomorphism classes of torsors over the smooth group scheme
$G/G^{\geq 2}\buildrel {\sim }\over {\longrightarrow } G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$ is identified with the set of isomorphism classes of torsors over the smooth group scheme ![]() $\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$ over
$\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$ over ![]() $X'$. The latter group scheme is identified with the quotient of the group scheme of invertible elements in the sheaf of
$X'$. The latter group scheme is identified with the quotient of the group scheme of invertible elements in the sheaf of ![]() ${\mathcal {O}}_{X'}$-algebras
${\mathcal {O}}_{X'}$-algebras ![]() $F_*{\mathcal {O}}_X$ by constant group scheme
$F_*{\mathcal {O}}_X$ by constant group scheme ![]() ${\mathbb {G}}_m \times X'$. Using smoothness of
${\mathbb {G}}_m \times X'$. Using smoothness of ![]() $\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$ every torsor over this group scheme is locally trivial for the étale topology on
$\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$ every torsor over this group scheme is locally trivial for the étale topology on ![]() $X'$. Hence, the set of isomorphism classes of
$X'$. Hence, the set of isomorphism classes of ![]() $\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$-torsors is in bijection with
$\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$-torsors is in bijection with ![]() $H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{p *})$. This defines a map of sets
$H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{p *})$. This defines a map of sets
from the set ![]() $Q(X, [\eta ])$ of isomorphisms classes of Frobenius-constant quantizations
$Q(X, [\eta ])$ of isomorphisms classes of Frobenius-constant quantizations ![]() $(X, {\mathcal {O}}_h, s)$ compatible with
$(X, {\mathcal {O}}_h, s)$ compatible with ![]() $[\eta ]$ to the étale cohomology group classifying torsors over
$[\eta ]$ to the étale cohomology group classifying torsors over ![]() $G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$ lifting the
$G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$ lifting the ![]() $G_0$-torsor
$G_0$-torsor ![]() ${\mathcal {M}}_{X, [\eta ]}$. Note that under this identification the trivial cohomology class corresponds to the lifting obtained from
${\mathcal {M}}_{X, [\eta ]}$. Note that under this identification the trivial cohomology class corresponds to the lifting obtained from ![]() ${\mathcal {M}}_{X, [\eta ]}$ via the natural group homomorphism
${\mathcal {M}}_{X, [\eta ]}$ via the natural group homomorphism ![]() $G_0 \to G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$.
$G_0 \to G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$.
Next, the obstruction class to lifting of a ![]() $G/G^{\geq n}$-torsor, with
$G/G^{\geq n}$-torsor, with ![]() $n>1$, to a
$n>1$, to a ![]() $G/G^{\geq n+1}$-torsor lies in
$G/G^{\geq n+1}$-torsor lies in ![]() $H^2(X', {\mathcal {O}}_{X'} /{\mathcal {O}}_{X'}^p)$. If the obstruction class vanishes, then the set of isomorphism classes of the liftings is a torsor over
$H^2(X', {\mathcal {O}}_{X'} /{\mathcal {O}}_{X'}^p)$. If the obstruction class vanishes, then the set of isomorphism classes of the liftings is a torsor over ![]() $H^1(X', {\mathcal {O}}_{X'} /{\mathcal {O}}_{X'}^p)$. Hence, if
$H^1(X', {\mathcal {O}}_{X'} /{\mathcal {O}}_{X'}^p)$. Hence, if ![]() $H^1_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then
$H^1_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then ![]() $\rho$ is injective, and if
$\rho$ is injective, and if ![]() $H^2_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then
$H^2_{\rm Zar}(X', {\mathcal {O}}_{X'}/{\mathcal {O}}_{X'}^p )=0$, then ![]() $\rho$ is surjective. In particular, if the two cohomology groups vanish
$\rho$ is surjective. In particular, if the two cohomology groups vanish ![]() $\rho$ is a bijection. The trivial cohomology class corresponds to a quantization that admits (a unique)
$\rho$ is a bijection. The trivial cohomology class corresponds to a quantization that admits (a unique) ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant structure.
${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant structure.
3. Reduction of the main theorem to a group-theoretic statement
In this section we recast the construction of ![]() ${\mathcal {D}}_{X, [\eta ], h}$ using the language of formal geometry, and reduce Theorem 1 to a certain statement, Proposition 3.3, on central extensions of the group of automorphisms of the restricted Weyl algebra.
${\mathcal {D}}_{X, [\eta ], h}$ using the language of formal geometry, and reduce Theorem 1 to a certain statement, Proposition 3.3, on central extensions of the group of automorphisms of the restricted Weyl algebra.
3.1  ${\mathcal {D}}_{X, [\eta ], h}$ via formal geometry
${\mathcal {D}}_{X, [\eta ], h}$ via formal geometry
Let ![]() $A_h^{\flat }$ be the reduced Weyl algebra in
$A_h^{\flat }$ be the reduced Weyl algebra in ![]() $4n$ variables, that is, the
$4n$ variables, that is, the ![]() $k[[h]]$-algebra generated by variables
$k[[h]]$-algebra generated by variables ![]() $x_i, y_i, v_i, u_i$
$x_i, y_i, v_i, u_i$ ![]() $(1\leq i,j, \leq n)$, subject to the relations
$(1\leq i,j, \leq n)$, subject to the relations
 \begin{gather} \begin{gathered} v_i x_j
- x_j v_i = u_i y_j - y_j u_i =\delta_{ij} h, \\ v_i y_j -
y_j v_i = u_i x_j - x_j u_i = v_i u_j - u_j v_i = y_i x_j -
x_j y_i =0, \\ x_i^{p} = y_i^{p}= v_i^{p} = u_i^{p} =0.
\end{gathered} \end{gather}
\begin{gather} \begin{gathered} v_i x_j
- x_j v_i = u_i y_j - y_j u_i =\delta_{ij} h, \\ v_i y_j -
y_j v_i = u_i x_j - x_j u_i = v_i u_j - u_j v_i = y_i x_j -
x_j y_i =0, \\ x_i^{p} = y_i^{p}= v_i^{p} = u_i^{p} =0.
\end{gathered} \end{gather}
We shall identify ![]() $A_h^{\flat }$ with the central reduction
$A_h^{\flat }$ with the central reduction ![]() $D_{\operatorname {Spec} A_0, \eta _A, h} (= D_{\operatorname {Spec} A_0, 0, h})$,
$D_{\operatorname {Spec} A_0, \eta _A, h} (= D_{\operatorname {Spec} A_0, 0, h})$, ![]() $\eta _A =\eta =\sum y_i\,dx_i$, of the algebra
$\eta _A =\eta =\sum y_i\,dx_i$, of the algebra ![]() $D_{\operatorname {Spec} A_0, h}\subset D_{\operatorname {Spec} A_0}[[h]]$ spanned by
$D_{\operatorname {Spec} A_0, h}\subset D_{\operatorname {Spec} A_0}[[h]]$ spanned by ![]() $A_0$ and
$A_0$ and ![]() $h T_{\operatorname {Spec} A_0}$. In particular, the group scheme
$h T_{\operatorname {Spec} A_0}$. In particular, the group scheme ![]() $\underline {\operatorname {Aut}} (A_0)$ acts on
$\underline {\operatorname {Aut}} (A_0)$ acts on ![]() $A_h^{\flat }$:
$A_h^{\flat }$:
We define a homomorphism
to be the restriction of ![]() $\psi _{{\rm can}}$ to
$\psi _{{\rm can}}$ to ![]() $G_0 \subset \underline {\operatorname {Aut}} (A_0)$ twisted by a
$G_0 \subset \underline {\operatorname {Aut}} (A_0)$ twisted by a ![]() $1$-cocycle
$1$-cocycle
Namely, for any ![]() $k$-algebra
$k$-algebra ![]() $R$, an
$R$, an ![]() $R$-point of
$R$-point of ![]() $G_0$ is an automorphism
$G_0$ is an automorphism ![]() $g$ of the
$g$ of the ![]() $R$-algebra
$R$-algebra ![]() $A_0\otimes R$ such that the
$A_0\otimes R$ such that the ![]() $1$-form
$1$-form ![]() $\mu := g^* \eta - \eta \in \Omega _{A_0\otimes R/R} ^1$,
$\mu := g^* \eta - \eta \in \Omega _{A_0\otimes R/R} ^1$, ![]() $\eta =\sum y_i \,dx_i$, is exact. Let
$\eta =\sum y_i \,dx_i$, is exact. Let ![]() $\phi _\mu : A_h^{\flat } \hat {\otimes } R \to A_h^{\flat } \hat {\otimes } R$ be the
$\phi _\mu : A_h^{\flat } \hat {\otimes } R \to A_h^{\flat } \hat {\otimes } R$ be the ![]() $R[[h]]$-algebra automorphism given by the formulasFootnote 8
$R[[h]]$-algebra automorphism given by the formulasFootnote 8
Define (3.3) by the formula
We claim that (3.3) is a homomorphism. Indeed, one has that
Using this formula we find
and the claim follows.
The key assertion of this subsection is the following.
Lemma 3.1 Let ![]() $(X, \omega )$ be a symplectic variety with a restricted Poisson structure
$(X, \omega )$ be a symplectic variety with a restricted Poisson structure ![]() $[\eta ]$. Then one has an isomorphism of
$[\eta ]$. Then one has an isomorphism of ![]() ${\mathcal {O}}_{X'}[[h]]$-algebras:
${\mathcal {O}}_{X'}[[h]]$-algebras:
where the action of ![]() $G_0$ on
$G_0$ on ![]() $A_h^{\flat }$ is given by (3.3).
$A_h^{\flat }$ is given by (3.3).
Proof. Let ![]() $\pi : {\mathcal {M}}_{X, [\eta ]} \rightarrow X^{\prime }$ be the projection. For a morphism
$\pi : {\mathcal {M}}_{X, [\eta ]} \rightarrow X^{\prime }$ be the projection. For a morphism ![]() $u\colon T \to X'$, we shall denote by
$u\colon T \to X'$, we shall denote by ![]() $u^* {\mathcal {D}}_{X, h, [\eta ]}$ the pullback
$u^* {\mathcal {D}}_{X, h, [\eta ]}$ the pullback ![]() ${\mathcal {D}}_{X, h, [\eta ]}$, viewed as a coherent sheaf on the formal scheme
${\mathcal {D}}_{X, h, [\eta ]}$, viewed as a coherent sheaf on the formal scheme ![]() $X'[[h]]$, along the morphism
$X'[[h]]$, along the morphism ![]() $T[[h]] \to X'[[h]]$ induced by
$T[[h]] \to X'[[h]]$ induced by ![]() $u$. It suffices to check that for every
$u$. It suffices to check that for every ![]() $S$-point
$S$-point ![]() $f$ of
$f$ of ![]() ${\mathcal {M}}_{X, [\eta ]}$ there is an isomorphism
${\mathcal {M}}_{X, [\eta ]}$ there is an isomorphism
such that the following diagram is commutative for every ![]() $g\in G_0(S)$.
$g\in G_0(S)$.

Construct ![]() $\alpha _f$ as follows. By definition of
$\alpha _f$ as follows. By definition of ![]() ${\mathcal {M}}_{X, [\eta ]}$ the point
${\mathcal {M}}_{X, [\eta ]}$ the point ![]() $f$ determines an isomorphism
$f$ determines an isomorphism ![]() $S \times \operatorname {Spec}(A_0) \buildrel {\sim }\over {\longrightarrow } S \times _{X^{\prime }} X$ also denoted by
$S \times \operatorname {Spec}(A_0) \buildrel {\sim }\over {\longrightarrow } S \times _{X^{\prime }} X$ also denoted by ![]() $f$ fitting into the following commutative diagram.
$f$ fitting into the following commutative diagram.

This induces an isomorphism of the corresponding algebras of differential operators:
Applying the Artin–Rees construction we get
First, we assume that the class ![]() $[\eta ]$ is represented by a global
$[\eta ]$ is represented by a global ![]() $1$-form
$1$-form ![]() $\eta$. Then the sheaf
$\eta$. Then the sheaf ![]() ${\mathcal {D}}_{X, h, [\eta ]}$ is obtained from
${\mathcal {D}}_{X, h, [\eta ]}$ is obtained from ![]() $D_{X, h}$ as the
$D_{X, h}$ as the ![]() $h$-completion of the quotient
$h$-completion of the quotient ![]() $D_{X, h}/I_{\Gamma _{\eta }}D_{X, h}$ (see formula (1.6)). The algebra
$D_{X, h}/I_{\Gamma _{\eta }}D_{X, h}$ (see formula (1.6)). The algebra ![]() $A_h^{\flat }$ is the quotient
$A_h^{\flat }$ is the quotient ![]() $D_{A_0, h}/I_{\Gamma _{\eta _A}}D_{A_0, h}$. The desired isomorphism
$D_{A_0, h}/I_{\Gamma _{\eta _A}}D_{A_0, h}$. The desired isomorphism ![]() $\alpha _f$ is defined from the following commutative diagram.
$\alpha _f$ is defined from the following commutative diagram.

One checks that ![]() $\alpha _f$ is independent of the choice of representative
$\alpha _f$ is independent of the choice of representative ![]() $\eta$ for
$\eta$ for ![]() $[\eta ]$. Therefore, covering
$[\eta ]$. Therefore, covering ![]() $X'$ by open subsets where
$X'$ by open subsets where ![]() $[\eta ]$ is represented by a
$[\eta ]$ is represented by a ![]() $1$-form, we can patch
$1$-form, we can patch ![]() $\alpha _f$ from local pieces. The compatibility with the action of
$\alpha _f$ from local pieces. The compatibility with the action of ![]() $G_0$ is straightforward.
$G_0$ is straightforward.
3.2 Central extensions of  $G$
$G$
Consider the action of the ![]() $k[[h]]$-algebra
$k[[h]]$-algebra ![]() $A_h$ on the free
$A_h$ on the free ![]() $k[[h]]$-module
$k[[h]]$-module ![]() $k[x_1, \ldots, x_{n}]/(x_1^p, \ldots, x_{n}^p)[[h]]$ given by the formulas
$k[x_1, \ldots, x_{n}]/(x_1^p, \ldots, x_{n}^p)[[h]]$ given by the formulas
It is well known (see e.g. [Reference Bezrukavnikov, Mirkovic and RumyninBMR02, Lemma 2.2.1]) and easy to verify that this action defines an isomorphism of ![]() $k((h))$-algebras
$k((h))$-algebras
For any ![]() $k$-algebra
$k$-algebra ![]() $R$, isomorphism (3.4) gives rise to a natural homomorphism
$R$, isomorphism (3.4) gives rise to a natural homomorphism
This defines an embedding
where ![]() $L\operatorname {PGL}(p^n)$ is the loop group of
$L\operatorname {PGL}(p^n)$ is the loop group of ![]() $\operatorname {PGL}(p^n)$, that is a sheaf of groups on the category of affine schemes of over
$\operatorname {PGL}(p^n)$, that is a sheaf of groups on the category of affine schemes of over ![]() $k$ equipped with the fpqc topology sending
$k$ equipped with the fpqc topology sending ![]() $k$-scheme
$k$-scheme ![]() $\operatorname {Spec} R$ to
$\operatorname {Spec} R$ to ![]() $\operatorname {PGL}(p^n, R((h)))$. The natural morphism of algebraic groups
$\operatorname {PGL}(p^n, R((h)))$. The natural morphism of algebraic groups ![]() $\operatorname {GL}(p^n) \to \operatorname {PGL}(p^n)$ gives rise to a morphism of the loop groups
$\operatorname {GL}(p^n) \to \operatorname {PGL}(p^n)$ gives rise to a morphism of the loop groups ![]() $L\operatorname {GL}(p^n) \to L\operatorname {PGL}(p^n)$. By part (i) of Proposition A.5 in the pullback diagram of fpqc sheaves
$L\operatorname {GL}(p^n) \to L\operatorname {PGL}(p^n)$. By part (i) of Proposition A.5 in the pullback diagram of fpqc sheaves

the left vertical arrow is surjective. Thus, we have a central extension of fpqc sheaves
Recall from § 2.4 that subgroup ![]() $G^{\geq 1}\subset G$ of automorphisms identical modulo
$G^{\geq 1}\subset G$ of automorphisms identical modulo ![]() $h$ consists of inner automorphisms. Therefore, extension (3.6) fits into a commutative diagram
$h$ consists of inner automorphisms. Therefore, extension (3.6) fits into a commutative diagram

where ![]() $\widetilde {G}_0 = \widetilde {G}/ \underline {A}_h ^*$ and
$\widetilde {G}_0 = \widetilde {G}/ \underline {A}_h ^*$ and ![]() $\operatorname {Gr}_{\mathbb {G}_m}= L{\mathbb {G}}_m/ L^+{\mathbb {G}}_m$ is the affine grassmannian for
$\operatorname {Gr}_{\mathbb {G}_m}= L{\mathbb {G}}_m/ L^+{\mathbb {G}}_m$ is the affine grassmannian for ![]() ${\mathbb {G}}_m$.
${\mathbb {G}}_m$.
Remark 3.2 Consider the central extension of the Lie algebras
corresponding to the bottom line in the diagram above. Identify the Lie algebra of the affine grassmannian with the vector space ![]() $h^{-1} k[h^{-1} ]$ of polynomial vanishing at the origin equipped with the trivial Lie bracket. It is shown in [Reference Bezrukavnikov and KaledinBK08] that the Lie algebra of
$h^{-1} k[h^{-1} ]$ of polynomial vanishing at the origin equipped with the trivial Lie bracket. It is shown in [Reference Bezrukavnikov and KaledinBK08] that the Lie algebra of ![]() $G_0$ consists of Hamiltonian vector fields on
$G_0$ consists of Hamiltonian vector fields on ![]() $A_0$, that is,
$A_0$, that is, ![]() $\operatorname {Lie} G_0 = A_0/k$, where the Lie bracket is induced by the Poisson bracket on
$\operatorname {Lie} G_0 = A_0/k$, where the Lie bracket is induced by the Poisson bracket on ![]() $A_0$. Then
$A_0$. Then ![]() $\operatorname {Lie} \widetilde {G}_0$ is isomorphic to the direct sum of Lie algebras
$\operatorname {Lie} \widetilde {G}_0$ is isomorphic to the direct sum of Lie algebras ![]() $A_0 \oplus h^{-2} k[h^{-1} ]$ with map to
$A_0 \oplus h^{-2} k[h^{-1} ]$ with map to ![]() $\operatorname {Lie} G_0$ given by the projection to the first summand followed by
$\operatorname {Lie} G_0$ given by the projection to the first summand followed by ![]() $A_0 \to A_0/k$.
$A_0 \to A_0/k$.
Proof. It suffices to construct a morphism of extensions as follows.

Define ![]() $A_0 \to \operatorname {Lie}(\widetilde {G}_0)$ that coincides with the map
$A_0 \to \operatorname {Lie}(\widetilde {G}_0)$ that coincides with the map ![]() $A_0 / k \to \operatorname {Lie}(G_0)$ sending
$A_0 / k \to \operatorname {Lie}(G_0)$ sending ![]() $a \in A_0$ to
$a \in A_0$ to ![]() $\operatorname {Ad}_{1 + {\epsilon \tilde {a}}/{h}} \in \widetilde {G}(k[\epsilon ]/\epsilon ^2) \to \widetilde G_0(k[\epsilon ]/\epsilon ^2)$, where
$\operatorname {Ad}_{1 + {\epsilon \tilde {a}}/{h}} \in \widetilde {G}(k[\epsilon ]/\epsilon ^2) \to \widetilde G_0(k[\epsilon ]/\epsilon ^2)$, where ![]() $\tilde {a} \in A_h$ is any lifting of
$\tilde {a} \in A_h$ is any lifting of ![]() $a$.
$a$.
Applying the same construction to the algebra ![]() $A_h^{\flat }$ and to its representation on
$A_h^{\flat }$ and to its representation on ![]() $k[x_1, \ldots, x_{n}, y_1, \ldots, y_{n}]/(x_1^p, \ldots, x_{n}^p, y_1^p, \ldots, y_{n}^p)[[h]]$ we construct the following commutative diagram.
$k[x_1, \ldots, x_{n}, y_1, \ldots, y_{n}]/(x_1^p, \ldots, x_{n}^p, y_1^p, \ldots, y_{n}^p)[[h]]$ we construct the following commutative diagram.

Recall from (3.3) the homomorphism ![]() $\psi : G_0 \to G^\flat$. Denote by
$\psi : G_0 \to G^\flat$. Denote by ![]() $\psi _0: G_0 \to G_0 ^\flat$ its composition with the projection
$\psi _0: G_0 \to G_0 ^\flat$ its composition with the projection ![]() $G^\flat \to G^\flat _0$. The key step in the proof of our main theorem is the following result.
$G^\flat \to G^\flat _0$. The key step in the proof of our main theorem is the following result.
Proposition 3.3 There is a unique homomorphism ![]() $\tilde {\psi }_0$ making the following diagram commutative.
$\tilde {\psi }_0$ making the following diagram commutative.

Remark 3.4 Let us describe the morphism of the Lie algebras induced by ![]() $\tilde {\psi _0}$. Namely, define
$\tilde {\psi _0}$. Namely, define ![]() $d(\tilde {\psi _0}) : f \mapsto f + \eta (H_f) + \mathcal {H}_f$. Here
$d(\tilde {\psi _0}) : f \mapsto f + \eta (H_f) + \mathcal {H}_f$. Here ![]() $H_f$ denotes the Hamiltonian vector field on
$H_f$ denotes the Hamiltonian vector field on ![]() $A_0$, while
$A_0$, while ![]() $\mathcal {H}_f$ is the same vector field viewed as a function on
$\mathcal {H}_f$ is the same vector field viewed as a function on ![]() $A_0^{\flat }$.
$A_0^{\flat }$.
We end this subsection with a reformulation of Proposition 3.3 that will be used in forthcoming paper [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22]. Set ![]() $B_h= A_h \otimes _{k[[h]]} A_h^{\flat, {\rm op}}$. Let
$B_h= A_h \otimes _{k[[h]]} A_h^{\flat, {\rm op}}$. Let
be the preimage of ![]() $\Gamma _{\psi _0}: G_0 \hookrightarrow \underline {\operatorname {Aut}} (B_0)= \underline {\operatorname {Aut}} (A_0 \otimes A_0^\flat )$,
$\Gamma _{\psi _0}: G_0 \hookrightarrow \underline {\operatorname {Aut}} (B_0)= \underline {\operatorname {Aut}} (A_0 \otimes A_0^\flat )$, ![]() $\Gamma _{\psi _0}(g)= g\otimes \psi _0(g)$. Proposition 3.3 implies that the canonical extension of
$\Gamma _{\psi _0}(g)= g\otimes \psi _0(g)$. Proposition 3.3 implies that the canonical extension of ![]() $\underline {\operatorname {Aut}} (B_h)$ by
$\underline {\operatorname {Aut}} (B_h)$ by ![]() $L{\mathbb {G}}_m$ (cf. (3.6)) restricted to
$L{\mathbb {G}}_m$ (cf. (3.6)) restricted to ![]() $G^\sharp$ admits a unique reduction to
$G^\sharp$ admits a unique reduction to ![]() $L^+{\mathbb {G}}_m$:
$L^+{\mathbb {G}}_m$:
Corollary 3.5 There exists a unique (up to a unique isomorphism) triple ![]() $(\widehat {G}^\sharp, \alpha, i)$ displayed in the diagram
$(\widehat {G}^\sharp, \alpha, i)$ displayed in the diagram

where the north east arrow is the natural inclusion, ![]() $i$ is a monomorphism and
$i$ is a monomorphism and ![]() $\alpha (g)= \operatorname {Ad}_{i(g)}$. In addition, if
$\alpha (g)= \operatorname {Ad}_{i(g)}$. In addition, if ![]() $W$ is an irreducible representation of
$W$ is an irreducible representation of ![]() $B_h(h^{-1})$,
$B_h(h^{-1})$, ![]() $B_h(h^{-1}) \buildrel {\sim }\over {\longrightarrow } \operatorname {End}_{k((h))}(W)$, there exists a
$B_h(h^{-1}) \buildrel {\sim }\over {\longrightarrow } \operatorname {End}_{k((h))}(W)$, there exists a ![]() $k[[h]]$-lattice
$k[[h]]$-lattice ![]() $\Lambda \subset W$, invariant under the
$\Lambda \subset W$, invariant under the ![]() $B_h$-action on
$B_h$-action on ![]() $W$ and under the action of
$W$ and under the action of ![]() $\widehat {G}^\sharp$:
$\widehat {G}^\sharp$:
3.3 Proposition 3.3 implies the main theorem
In this subsection we prove Theorem 1 assuming Proposition 3.3.
For the first part, let us start by reinterpreting the construction of the algebra ![]() ${\mathcal {O}}_h \otimes _{{\mathcal {O}}_{X'}[[h]]} {\mathcal {D}}_{X, [\eta ], h}^{\rm {\rm op}}$. Consider the homomorphism
${\mathcal {O}}_h \otimes _{{\mathcal {O}}_{X'}[[h]]} {\mathcal {D}}_{X, [\eta ], h}^{\rm {\rm op}}$. Consider the homomorphism
whose first component is the identity map and whose second component is the composition ![]() $G \stackrel {}{\longrightarrow } G_0 \stackrel {\psi }{\longrightarrow } \operatorname {Aut}_{k[[h]]}(A_h^{\flat })= \operatorname {Aut}_{k[[h]]}(A_h^{\flat, {\rm op}})$.Footnote 9 Homomorphism (3.9) defines a sheaf of
$G \stackrel {}{\longrightarrow } G_0 \stackrel {\psi }{\longrightarrow } \operatorname {Aut}_{k[[h]]}(A_h^{\flat })= \operatorname {Aut}_{k[[h]]}(A_h^{\flat, {\rm op}})$.Footnote 9 Homomorphism (3.9) defines a sheaf of ![]() ${\mathcal {O}}_{X'}[[h]]$-algebras
${\mathcal {O}}_{X'}[[h]]$-algebras ![]() ${\mathcal {M}}_{X, {\mathcal {O}}_h, s} \times _G (A_h\otimes _{k[[h]]} A_h^{\flat, {\rm op}})$. By Lemma 3.1, we have an isomorphism
${\mathcal {M}}_{X, {\mathcal {O}}_h, s} \times _G (A_h\otimes _{k[[h]]} A_h^{\flat, {\rm op}})$. By Lemma 3.1, we have an isomorphism
Next, the ![]() $k((h))$-algebra
$k((h))$-algebra ![]() $(A_h\otimes _{k[[h]]} A_h^{\flat, {\rm op}})(h^{-1})$ is isomorphic to the matrix algebra
$(A_h\otimes _{k[[h]]} A_h^{\flat, {\rm op}})(h^{-1})$ is isomorphic to the matrix algebra ![]() $\operatorname {End}_{k((h))}(V)$, for some vector space over
$\operatorname {End}_{k((h))}(V)$, for some vector space over ![]() $k((h))$ of dimension
$k((h))$ of dimension ![]() $p^{3n}$:
$p^{3n}$:
Isomorphisms (3.10) and (3.9) give rise to a homomorphism
and, consequently, to an extension of ![]() $G$ by
$G$ by ![]() $L{\mathbb {G}}_m$. Proposition 3.3 asserts that this extension admits a unique reduction to
$L{\mathbb {G}}_m$. Proposition 3.3 asserts that this extension admits a unique reduction to ![]() $L^+{\mathbb {G}}_m$.
$L^+{\mathbb {G}}_m$.
Thus, by part (ii) of Proposition A.5, it follows that homomorphism (3.11), possibly after conjugation by an element of ![]() $\operatorname {PGL}(p^{3n}, k((h)))$, factors through
$\operatorname {PGL}(p^{3n}, k((h)))$, factors through ![]() $L^+\operatorname {PGL}(p^{3n})\subset L\operatorname {PGL}(p^{3n})$. In the other words, there exists a
$L^+\operatorname {PGL}(p^{3n})\subset L\operatorname {PGL}(p^{3n})$. In the other words, there exists a ![]() $k[[h]]$-lattice
$k[[h]]$-lattice ![]() $\Lambda \subset V$ such that the action of
$\Lambda \subset V$ such that the action of ![]() $G$ on
$G$ on ![]() $(A_h\otimes _{k[[h]]} A_h^{\flat, {\rm op}})(h^{-1})$ preserves
$(A_h\otimes _{k[[h]]} A_h^{\flat, {\rm op}})(h^{-1})$ preserves ![]() $\operatorname {End}_{k[[h]]}(\Lambda )$:
$\operatorname {End}_{k[[h]]}(\Lambda )$:
The homomorphism
and the ![]() $G$-torsor
$G$-torsor ![]() ${\mathcal {M}}_{X, {\mathcal {O}}_h, s}$ give rise to an Azumaya algebra
${\mathcal {M}}_{X, {\mathcal {O}}_h, s}$ give rise to an Azumaya algebra
which, by construction, coincides with ![]() ${\mathcal {O}}_h \otimes _{{\mathcal {O}}_{X'}[[h]]} {\mathcal {D}}_{X, [\eta ], h}^{\rm op}$ after inverting
${\mathcal {O}}_h \otimes _{{\mathcal {O}}_{X'}[[h]]} {\mathcal {D}}_{X, [\eta ], h}^{\rm op}$ after inverting ![]() $h$. This proves part (i) of the Theorem.
$h$. This proves part (i) of the Theorem.
To prove part (ii) of the Theorem, recall from § 2.4 that ![]() $G$ is acted upon by an involution
$G$ is acted upon by an involution ![]() $\tau : G\to G$. We claim that
$\tau : G\to G$. We claim that ![]() $\tau$ lifts to extension (3.12),
$\tau$ lifts to extension (3.12),
such that the restriction of ![]() $\hat \tau$ to
$\hat \tau$ to ![]() $L^+{\mathbb {G}}_m$ is given by the formula
$L^+{\mathbb {G}}_m$ is given by the formula
Consider the homomorphism ![]() $L^+ {\mathbb {G}}_m \to {\mathbb {G}}_m$ sending
$L^+ {\mathbb {G}}_m \to {\mathbb {G}}_m$ sending ![]() $f(h)\in L^+ {\mathbb {G}}_m(R)= R[[h]]^*$ to
$f(h)\in L^+ {\mathbb {G}}_m(R)= R[[h]]^*$ to ![]() $f(0)\in R^*$. This fits into the following diagram of group scheme extensions.
$f(0)\in R^*$. This fits into the following diagram of group scheme extensions.

The action of ![]() $\hat {\tau }$ on
$\hat {\tau }$ on ![]() $\widehat {G}$ descends to
$\widehat {G}$ descends to ![]() $\widehat { G/G^{\geq 2} }$. For the
$\widehat { G/G^{\geq 2} }$. For the ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-action on
${\mathbb {Z}}/2{\mathbb {Z}}$-action on ![]() $R^*$ given by formula
$R^*$ given by formula ![]() $c\mapsto c^{-1}$, we have that
$c\mapsto c^{-1}$, we have that
In particular, every cohomology class gets killed after a finite étale extension of ![]() $R$. It follows that the sequence of
$R$. It follows that the sequence of ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-invariants
${\mathbb {Z}}/2{\mathbb {Z}}$-invariants
is exact. Note that ![]() ${\mathbb {G}}_m^{\hat \tau =1} = \mu _2 = \{1, -1\}$. We claim that (3.16) is a split extension:
${\mathbb {G}}_m^{\hat \tau =1} = \mu _2 = \{1, -1\}$. We claim that (3.16) is a split extension:
Indeed, the determinant homomorphism
composed with the map ![]() $L^+G_m \to {\mathbb {G}}_m$ factors through
$L^+G_m \to {\mathbb {G}}_m$ factors through ![]() $\widehat { G/G^{\geq 2} }$ and commutes with
$\widehat { G/G^{\geq 2} }$ and commutes with ![]() $\tau$. Hence, it defines a homomorphism
$\tau$. Hence, it defines a homomorphism
whose restriction to ![]() $\mu _2$ is the identity. This gives a splitting of extension (3.16). We derive from (3.17) that the extension
$\mu _2$ is the identity. This gives a splitting of extension (3.16). We derive from (3.17) that the extension ![]() $\widehat { G/G^{\geq 2} }$ has the form
$\widehat { G/G^{\geq 2} }$ has the form
Now we can prove that
To see this, consider the gerbe ![]() ${\mathcal {S}}$ of splittings of the Azumaya algebra
${\mathcal {S}}$ of splittings of the Azumaya algebra ![]() ${\mathcal {O}}^\sharp _h$. By definition, this is a sheaf of groupoids on
${\mathcal {O}}^\sharp _h$. By definition, this is a sheaf of groupoids on ![]() $(X')_{fl}$ whose sections
$(X')_{fl}$ whose sections ![]() ${\mathcal {S}}(Z)$ over
${\mathcal {S}}(Z)$ over ![]() $Z\to X'$ is the groupoid of splittings of the pullback of
$Z\to X'$ is the groupoid of splittings of the pullback of ![]() ${\mathcal {O}}^\sharp _h$ to
${\mathcal {O}}^\sharp _h$ to ![]() $Z$. This is a gerbe naturally banded by the sheaf
$Z$. This is a gerbe naturally banded by the sheaf ![]() $L^+{\mathbb {G}}_m$ meaning that the automorphism group of any object of
$L^+{\mathbb {G}}_m$ meaning that the automorphism group of any object of ![]() ${\mathcal {S}}(Z)$ is canonically identified with
${\mathcal {S}}(Z)$ is canonically identified with ![]() $L^+{\mathbb {G}}_m(Z)$. By construction of
$L^+{\mathbb {G}}_m(Z)$. By construction of ![]() ${\mathcal {O}}^\sharp _h$ and the uniqueness statement in Proposition 3.3 this gerbe is equivalent to the gerbe of liftings of
${\mathcal {O}}^\sharp _h$ and the uniqueness statement in Proposition 3.3 this gerbe is equivalent to the gerbe of liftings of ![]() $G$-torsor
$G$-torsor ![]() ${\mathcal {M}}_{X, {\mathcal {O}}_h, s}$ to a
${\mathcal {M}}_{X, {\mathcal {O}}_h, s}$ to a ![]() $\widehat {G}$-torsor. It follows that the gerbe of splittings
$\widehat {G}$-torsor. It follows that the gerbe of splittings ![]() $\overline {{\mathcal {S}}}$ of the Azumaya algebra
$\overline {{\mathcal {S}}}$ of the Azumaya algebra ![]() $i^* {\mathcal {O}}^\sharp _h$ is equivalent to the
$i^* {\mathcal {O}}^\sharp _h$ is equivalent to the ![]() ${\mathbb {G}}_m$-gerbe of liftings of
${\mathbb {G}}_m$-gerbe of liftings of ![]() $G/G^{\geq 2}$-torsor
$G/G^{\geq 2}$-torsor ![]() ${\mathcal {L}}:= {\mathcal {M}}_{X, {\mathcal {O}}_h, s}\times _G G/G^{\geq 2}$ to a
${\mathcal {L}}:= {\mathcal {M}}_{X, {\mathcal {O}}_h, s}\times _G G/G^{\geq 2}$ to a ![]() $\widehat {G/G^{\geq 2} }$-torsor. The set of isomorphism classes of torsors over
$\widehat {G/G^{\geq 2} }$-torsor. The set of isomorphism classes of torsors over ![]() $G/G^{\geq 2}\buildrel {\sim }\over {\longrightarrow } G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$ lifting a given
$G/G^{\geq 2}\buildrel {\sim }\over {\longrightarrow } G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$ lifting a given ![]() $G_0$-torsor
$G_0$-torsor ![]() ${\mathcal {M}}_{X, [\eta ]}$ is in bijection
${\mathcal {M}}_{X, [\eta ]}$ is in bijection ![]() $\rho$ with the set
$\rho$ with the set ![]() $H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{p *})$ of isomorphism classes of torsors over the group scheme
$H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{p *})$ of isomorphism classes of torsors over the group scheme ![]() $\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$. It follows from (3.20) that given a
$\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$. It follows from (3.20) that given a ![]() $G/G^{\geq 2}$-torsor
$G/G^{\geq 2}$-torsor ![]() ${\mathcal {L}}$ the
${\mathcal {L}}$ the ![]() ${\mathbb {G}}_m$-gerbe of liftings of
${\mathbb {G}}_m$-gerbe of liftings of ![]() ${\mathcal {L}}$ to a torsor over
${\mathcal {L}}$ to a torsor over ![]() $\widehat {G/G^{\geq 2} }$ is equivalent to the gerbe of liftings of
$\widehat {G/G^{\geq 2} }$ is equivalent to the gerbe of liftings of ![]() $\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$-torsor
$\underline {A}_0^*/{\mathbb {G}}_m \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$-torsor ![]() $\rho ({\mathcal {L}})$ to a torsor over
$\rho ({\mathcal {L}})$ to a torsor over ![]() $\underline {A}_0^* \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$. This proves (3.21).
$\underline {A}_0^* \times _{G_0} {\mathcal {M}}_{X, [\eta ]}$. This proves (3.21).
To prove the last assertion of Theorem 1 observe that the kernel of the restriction ![]() $i^*\colon \operatorname {Br}(X'[[h]]) \to \operatorname {Br}(X')$ is a subgroup of the group
$i^*\colon \operatorname {Br}(X'[[h]]) \to \operatorname {Br}(X')$ is a subgroup of the group ![]() $H^2_{\rm Zar}(X', {\mathbb {W}}({\mathcal {O}}_{X'}))$, where
$H^2_{\rm Zar}(X', {\mathbb {W}}({\mathcal {O}}_{X'}))$, where ![]() ${\mathbb {W}}({\mathcal {O}}_{X'})$ is the additive group of the ring of big Witt vectors, that is,
${\mathbb {W}}({\mathcal {O}}_{X'})$ is the additive group of the ring of big Witt vectors, that is,
We claim that vanishing of ![]() $H^2(X', {\mathcal {O}}_{X'})$ implies vanishing of
$H^2(X', {\mathcal {O}}_{X'})$ implies vanishing of ![]() $H^2(X', {\mathbb {W}}({\mathcal {O}}_{X'}))$. Indeed,
$H^2(X', {\mathbb {W}}({\mathcal {O}}_{X'}))$. Indeed, ![]() ${\mathbb {W}}({\mathcal {O}}_{X'})$ is the inverse limit of the groups of truncated Witt vectors
${\mathbb {W}}({\mathcal {O}}_{X'})$ is the inverse limit of the groups of truncated Witt vectors
Using the exact sequence
it follows that, for every positive integer ![]() $m$, the group
$m$, the group ![]() $H^2(X, {\mathbb {W}}_m({\mathcal {O}}_{X'}))$ is trivial and consequently the restriction homomorphism
$H^2(X, {\mathbb {W}}_m({\mathcal {O}}_{X'}))$ is trivial and consequently the restriction homomorphism
is surjective, for every ![]() $l$ and
$l$ and ![]() $m$. Hence, by Proposition 13.3.1 from [Reference Grothendieck and DieudonneEGA III, Chapter 0], we have
$m$. Hence, by Proposition 13.3.1 from [Reference Grothendieck and DieudonneEGA III, Chapter 0], we have
as desired.
Remark 3.6 Observe that under the assumptions of Theorem 1, we have that
Indeed, ![]() ${\mathcal {O}}^\sharp _h$ is an Azumaya algebra of rank
${\mathcal {O}}^\sharp _h$ is an Azumaya algebra of rank ![]() $p^{6n}$ and, hence, its class in the Brauer group is killed by
$p^{6n}$ and, hence, its class in the Brauer group is killed by ![]() $p^{3n}$. On the other hand, the class
$p^{3n}$. On the other hand, the class ![]() $\delta (\gamma ))$ is killed by
$\delta (\gamma ))$ is killed by ![]() $p$.
$p$.
Remark 3.7 The proof of Theorem 1 shows that vanishing of ![]() $H^2(X', {\mathcal {O}}_{X'})$ implies surjectivity of the map
$H^2(X', {\mathcal {O}}_{X'})$ implies surjectivity of the map ![]() $\rho$ (see formula (1.4)), which does not follow directly from the Bezrukavnikov–Kaledin theorem. Indeed, from (3.12) we derive an extension
$\rho$ (see formula (1.4)), which does not follow directly from the Bezrukavnikov–Kaledin theorem. Indeed, from (3.12) we derive an extension
Consider the ![]() $G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$-torsor
$G_0 \ltimes \underline {A}_0^*/{\mathbb {G}}_m$-torsor ![]() ${\mathcal {M}}$ corresponding to a restricted structure
${\mathcal {M}}$ corresponding to a restricted structure ![]() $[\eta ]$ and a class
$[\eta ]$ and a class ![]() $\gamma \in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$. Using that
$\gamma \in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$. Using that ![]() $H^2(X', {\mathcal {O}}_{X'})=0$ we infer that
$H^2(X', {\mathcal {O}}_{X'})=0$ we infer that ![]() ${\mathcal {M}}$ can be lifted to a
${\mathcal {M}}$ can be lifted to a ![]() $\widehat { G}/{\mathbb {G}}_m$-torsor
$\widehat { G}/{\mathbb {G}}_m$-torsor ![]() $\tilde {\mathcal {M}}$. Pushing forward the latter under the homomorphism
$\tilde {\mathcal {M}}$. Pushing forward the latter under the homomorphism ![]() $\widehat { G}/{\mathbb {G}}_m \to G$ we get a quantization with
$\widehat { G}/{\mathbb {G}}_m \to G$ we get a quantization with ![]() $\rho$-invariant
$\rho$-invariant ![]() $\gamma$.
$\gamma$.
Remark 3.8 In [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24] the authors erroneously assert the subgroup ![]() $G\hookrightarrow L\operatorname {PGL}(p^n)$ from (3.5) preserves a lattice, that is, possibly after conjugation by an element of
$G\hookrightarrow L\operatorname {PGL}(p^n)$ from (3.5) preserves a lattice, that is, possibly after conjugation by an element of ![]() $\operatorname {PGL}(p^{n}, k((h)))$, factors through
$\operatorname {PGL}(p^{n}, k((h)))$, factors through ![]() $L^+\operatorname {PGL}(p^{n})\subset L\operatorname {PGL}(p^{n})$. This claim led the authors to a mistake in the statement of Proposition 1.24. In fact, even the subgroup of translations
$L^+\operatorname {PGL}(p^{n})\subset L\operatorname {PGL}(p^{n})$. This claim led the authors to a mistake in the statement of Proposition 1.24. In fact, even the subgroup of translations ![]() $\operatorname {Spec} A_0= \alpha _p^{2n} \subset G$ does not admit an invariant lattice. This follows from the fact the commutator map
$\operatorname {Spec} A_0= \alpha _p^{2n} \subset G$ does not admit an invariant lattice. This follows from the fact the commutator map
arising from extension (3.6) is given by the formula ![]() $({1}/{h})\sum _i dy_i \wedge dx_i$, i.e. does not factor through
$({1}/{h})\sum _i dy_i \wedge dx_i$, i.e. does not factor through ![]() $\operatorname {Lie} L^+{\mathbb {G}}_m = k[[h]]$.
$\operatorname {Lie} L^+{\mathbb {G}}_m = k[[h]]$.
4. Central extensions of the group of Poisson automorphisms
In this section we prove Basic Lemma 4 and derive from it Proposition 3.3. For the duration of this section we fix a symplectic vector space ![]() $(V, \omega _V)$ of dimension
$(V, \omega _V)$ of dimension ![]() $2n$ and denote by
$2n$ and denote by ![]() $A_h$ the corresponding restricted Weyl algebra,
$A_h$ the corresponding restricted Weyl algebra, ![]() $G$ its group of automorphisms and
$G$ its group of automorphisms and ![]() $G_0$ the quotient of
$G_0$ the quotient of ![]() $G$ by the subgroup of automorphisms identical modulo
$G$ by the subgroup of automorphisms identical modulo ![]() $h$ viewed as a group scheme of automorphisms of
$h$ viewed as a group scheme of automorphisms of ![]() $A_0$ preserving the class
$A_0$ preserving the class ![]() $[\eta _V]$.
$[\eta _V]$.
4.1 Properties of  $G_0$
$G_0$
Recall from [Reference Bezrukavnikov and KaledinBK08, Proposition 3.4] that the reduced subgroup ![]() $G_0^0=(G_0)_{\rm red} \subset G_0$ is equal to the stabilizer of the point
$G_0^0=(G_0)_{\rm red} \subset G_0$ is equal to the stabilizer of the point ![]() $\operatorname {Spec} k \hookrightarrow \operatorname {Spec} A_0$: for every
$\operatorname {Spec} k \hookrightarrow \operatorname {Spec} A_0$: for every ![]() $k$-algebra
$k$-algebra ![]() $R$,
$R$, ![]() $G_0^0(R)$ is the subgroup of
$G_0^0(R)$ is the subgroup of ![]() $G_0(R)$ that consists of
$G_0(R)$ that consists of ![]() $R$-linear automorphisms of
$R$-linear automorphisms of ![]() $A_0 \otimes R$ that preserve the kernel of the homomorphism
$A_0 \otimes R$ that preserve the kernel of the homomorphism ![]() $A_0 \otimes R \to R$ induced by
$A_0 \otimes R \to R$ induced by ![]() $A_0 \to k$. According to [Reference Bezrukavnikov and KaledinBK08, Lemma 3.3] the Lie algebra of
$A_0 \to k$. According to [Reference Bezrukavnikov and KaledinBK08, Lemma 3.3] the Lie algebra of ![]() $G_0$ (respectively,
$G_0$ (respectively, ![]() $G_0^0$) is the algebra of all Hamiltonian vector fieldsFootnote 10 on
$G_0^0$) is the algebra of all Hamiltonian vector fieldsFootnote 10 on ![]() $\operatorname {Spec} A_0$ (respectively, the algebra of all Hamiltonian vector fields vanishing at
$\operatorname {Spec} A_0$ (respectively, the algebra of all Hamiltonian vector fields vanishing at ![]() $\operatorname {Spec} k \hookrightarrow \operatorname {Spec} A_0$). In particular, we have
$\operatorname {Spec} k \hookrightarrow \operatorname {Spec} A_0$). In particular, we have
where ![]() $m$ is the maximal ideal in
$m$ is the maximal ideal in ![]() $A_0$.
$A_0$.
Denote by ![]() $\alpha _p$ the Frobenius kernel on
$\alpha _p$ the Frobenius kernel on ![]() ${\mathbb {G}}_a$. The finite group scheme
${\mathbb {G}}_a$. The finite group scheme ![]() $\alpha := \alpha _p^{2n}$ acts on
$\alpha := \alpha _p^{2n}$ acts on ![]() $\operatorname {Spec} A_0 = \alpha$ by translations inducing the inclusion
$\operatorname {Spec} A_0 = \alpha$ by translations inducing the inclusion ![]() $\alpha \hookrightarrow G_0$. Observe that the product morphism
$\alpha \hookrightarrow G_0$. Observe that the product morphism
induces an isomorphism of the underlying schemes.
Lemma 4.1 The group schemes ![]() $G_0$ and
$G_0$ and ![]() $G_0^0$ are connected. Moreover, there is a surjective homomorphism
$G_0^0$ are connected. Moreover, there is a surjective homomorphism
whose kernel is a unipotent algebraic group.
Proof. It suffices to prove the assertions for the reduced group ![]() $G_0^0$. To show that
$G_0^0$. To show that ![]() $G_0^0$ is connected we consider the filtration
$G_0^0$ is connected we consider the filtration
by normal group subschemes of ![]() $G_0^0$ and prove that all the associated quotients are connected. Namely, for any
$G_0^0$ and prove that all the associated quotients are connected. Namely, for any ![]() $k$-algebra
$k$-algebra ![]() $R$, we set
$R$, we set
It is easy to see that this functor is representable by a normal group subscheme of ![]() $G_0^0$.
$G_0^0$.
The action of ![]() $G_0^0$ on the tangent space
$G_0^0$ on the tangent space ![]() $(m/m^2)^*$ preserves
$(m/m^2)^*$ preserves ![]() $\omega$. Thus, it gives rise to a monomorphism
$\omega$. Thus, it gives rise to a monomorphism
which is, in fact, an isomorphism because it has a section. In particular, we have that
To check that the other quotients are connected we construct injective homomorphisms
where ![]() $\underline {m^{i+2}/m^{i+3}}$ is the vector group associated to the space
$\underline {m^{i+2}/m^{i+3}}$ is the vector group associated to the space ![]() $m^{i+2}/m^{i+3}$ and then using (4.1) conclude that
$m^{i+2}/m^{i+3}$ and then using (4.1) conclude that ![]() $\alpha _i$ are isomorphisms. For the sake of brevity we only define
$\alpha _i$ are isomorphisms. For the sake of brevity we only define ![]() $\alpha _i$ on
$\alpha _i$ on ![]() $k$-points. Take
$k$-points. Take ![]() $\phi \in F^iG_0^0(k)$ and consider
$\phi \in F^iG_0^0(k)$ and consider ![]() $\phi ^* : A_0 \rightarrow A_0$. By definition,
$\phi ^* : A_0 \rightarrow A_0$. By definition, ![]() $\phi ^* = \operatorname {Id}\, {\rm mod}\ m^{i+1}$, so
$\phi ^* = \operatorname {Id}\, {\rm mod}\ m^{i+1}$, so ![]() $\phi ^* - \operatorname {Id}$ maps
$\phi ^* - \operatorname {Id}$ maps ![]() $m^r$ to
$m^r$ to ![]() $m^{i+r}$, for every
$m^{i+r}$, for every ![]() $r\geq 0$. Hence
$r\geq 0$. Hence ![]() $\phi ^* - \operatorname {Id}$ defines a homogeneous degree
$\phi ^* - \operatorname {Id}$ defines a homogeneous degree ![]() $i$ map
$i$ map ![]() $\theta _\phi : \oplus m^r/m^{r+1} = A \rightarrow A$ which is, in fact, a derivation. Let us show that
$\theta _\phi : \oplus m^r/m^{r+1} = A \rightarrow A$ which is, in fact, a derivation. Let us show that ![]() $\theta _\phi$ lies in a Lie algebra of
$\theta _\phi$ lies in a Lie algebra of ![]() $G_0^0$, i.e.
$G_0^0$, i.e. ![]() $L_{\theta _\phi }\eta$ is exact. Indeed, since
$L_{\theta _\phi }\eta$ is exact. Indeed, since ![]() $\phi \in G_0^0$ we have
$\phi \in G_0^0$ we have ![]() $\phi ^*\eta = \eta + dK$ for some
$\phi ^*\eta = \eta + dK$ for some ![]() $K\in A_0$. But then
$K\in A_0$. But then ![]() $L_{\theta _\phi }\eta = dK_{i+2}$, where
$L_{\theta _\phi }\eta = dK_{i+2}$, where ![]() $K_{i+2}$ is the homogeneous component of
$K_{i+2}$ is the homogeneous component of ![]() $K$ of degree
$K$ of degree ![]() $i+2$. It follows that
$i+2$. It follows that ![]() $\theta _\phi$ is Hamiltonian:
$\theta _\phi$ is Hamiltonian: ![]() $\iota _{\theta _\phi } \omega = \iota _{\theta _\phi } d \eta = d(K_{i+2} - \iota _{\theta _\phi } \eta )$. Set
$\iota _{\theta _\phi } \omega = \iota _{\theta _\phi } d \eta = d(K_{i+2} - \iota _{\theta _\phi } \eta )$. Set
Using the identity ![]() $\theta _{\phi \circ \psi } = \theta _\phi +\theta _\psi$, for every
$\theta _{\phi \circ \psi } = \theta _\phi +\theta _\psi$, for every ![]() $\phi, \psi \in F^iG_0^0(k)$, one checks that
$\phi, \psi \in F^iG_0^0(k)$, one checks that ![]() $\alpha$ is a group homomorphism and that it factors through
$\alpha$ is a group homomorphism and that it factors through ![]() $F^iG_0^0 / F^{i+1}G_0^0$. For the injectivity of (4.3) observe that
$F^iG_0^0 / F^{i+1}G_0^0$. For the injectivity of (4.3) observe that ![]() $\theta _\phi =0$ if and only if
$\theta _\phi =0$ if and only if ![]() $\phi \in F^{i+1}G_0^0(k)$.
$\phi \in F^{i+1}G_0^0(k)$.
From (4.3) we have that, for every ![]() $i\geq 1$,
$i\geq 1$,
If for some ![]() $i$ the inequality is strict, then using (4.2) we would have that
$i$ the inequality is strict, then using (4.2) we would have that ![]() $\dim G_0^0 < \dim _k m^{2}$ contradicting to (4.1). It follows that all
$\dim G_0^0 < \dim _k m^{2}$ contradicting to (4.1). It follows that all ![]() $\alpha _i$ are isomorphisms as desired.
$\alpha _i$ are isomorphisms as desired.
Recall from Lemma A.1Footnote 11 a decomposition
Corollary 4.2 The extension (1.15) admits a unique reduction to ![]() $\hat {{\mathbb {W}}} \subset \operatorname {Gr}_{{\mathbb {G}}_m}$. Notation:
$\hat {{\mathbb {W}}} \subset \operatorname {Gr}_{{\mathbb {G}}_m}$. Notation:
Proof. By Lemma 4.1 we have that ![]() $Hom(G_0, \underline {{\mathbb {Z}}})=0$. The uniqueness part follows. For the existence, note that the composition
$Hom(G_0, \underline {{\mathbb {Z}}})=0$. The uniqueness part follows. For the existence, note that the composition
factors through ![]() $\widetilde {G}_0$. We claim that setting
$\widetilde {G}_0$. We claim that setting ![]() $\widetilde G^e_0:= \ker (\tilde {G}_0 \to \underline {{\mathbb {Z}}})$ does the job. Indeed, the only assertion that requires a proof is the surjectivity of the projection
$\widetilde G^e_0:= \ker (\tilde {G}_0 \to \underline {{\mathbb {Z}}})$ does the job. Indeed, the only assertion that requires a proof is the surjectivity of the projection ![]() $\widetilde G^e _0 \to G_0$. By construction,
$\widetilde G^e _0 \to G_0$. By construction, ![]() $\widetilde G^e _0$ projects onto the kernel of the homomorphism
$\widetilde G^e _0$ projects onto the kernel of the homomorphism ![]() $G_0 \to \underline {{\mathbb {Z}}}/p^n$ induced by
$G_0 \to \underline {{\mathbb {Z}}}/p^n$ induced by ![]() $\widetilde G_0 \to \underline {{\mathbb {Z}}}$. But by Lemma 4.1 every such homomorphism is trivial.
$\widetilde G_0 \to \underline {{\mathbb {Z}}}$. But by Lemma 4.1 every such homomorphism is trivial.
Consider ![]() $m^2\subset A_0$ as a Lie subalgebra of
$m^2\subset A_0$ as a Lie subalgebra of ![]() $A_0$ equipped with Poisson bracket. Recall that
$A_0$ equipped with Poisson bracket. Recall that
is an isomorphism of Lie algebras. The grading on ![]() $A_0$ induces a grading on the Lie algebra
$A_0$ induces a grading on the Lie algebra ![]() $m^2$:
$m^2$:
such that the Lie bracket has degree ![]() $-2$.
$-2$.
Lemma 4.3 Isomorphism (4.4) induces
In particular, ![]() $[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$ has codimension
$[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$ has codimension ![]() $1$ in
$1$ in ![]() $\operatorname {Lie} G_0^0$. Moreover,
$\operatorname {Lie} G_0^0$. Moreover, ![]() $\operatorname {\mathfrak {sp}}(2n) = m^2/m^3$ together with any nonzero element
$\operatorname {\mathfrak {sp}}(2n) = m^2/m^3$ together with any nonzero element ![]() $z\in m^3/m^4$ generate the Lie algebra
$z\in m^3/m^4$ generate the Lie algebra ![]() $[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$.
$[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$.
Proof. By a direct computation the Poisson bracket of any two monomials of total degree ![]() $2n(p-1) +2$ is
$2n(p-1) +2$ is ![]() $0$ i.e.
$0$ i.e. ![]() $[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$ does not contain nonzero homogeneous elements of degree
$[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$ does not contain nonzero homogeneous elements of degree ![]() $2n(p-1)$. Hence,
$2n(p-1)$. Hence, ![]() $[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0] \subset \bigoplus _{2 \leq i < 2n(p-1)} m^i/m^{i+1}$. Since
$[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0] \subset \bigoplus _{2 \leq i < 2n(p-1)} m^i/m^{i+1}$. Since ![]() $[\operatorname {\mathfrak {sp}}(2n), \operatorname {\mathfrak {sp}}(2n)] = \operatorname {\mathfrak {sp}}(2n)$, we have that
$[\operatorname {\mathfrak {sp}}(2n), \operatorname {\mathfrak {sp}}(2n)] = \operatorname {\mathfrak {sp}}(2n)$, we have that ![]() $m^2/m^3 \subset [\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$. Also it is clear that
$m^2/m^3 \subset [\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$. Also it is clear that ![]() $[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$ contains at least one nonzero element of degree
$[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$ contains at least one nonzero element of degree ![]() $3$ (e.g.
$3$ (e.g. ![]() $\{x_1^2, x_1 y_1^2\}= 2 x_1^2 y_1$). To complete the proof of the lemma it suffices to verify that the Lie subalgebra
$\{x_1^2, x_1 y_1^2\}= 2 x_1^2 y_1$). To complete the proof of the lemma it suffices to verify that the Lie subalgebra ![]() ${\mathfrak g}$ generated by
${\mathfrak g}$ generated by ![]() $m^2/m^3$ and a nonzero element of degree
$m^2/m^3$ and a nonzero element of degree ![]() $3$ coincides with
$3$ coincides with ![]() $\bigoplus _{2 \leq i < 2n(p-1)} m^i/m^{i+1}$. We check by induction on
$\bigoplus _{2 \leq i < 2n(p-1)} m^i/m^{i+1}$. We check by induction on ![]() $d$ that
$d$ that ![]() $m^d /m^{d+1}\subset {\mathfrak g}$ provided that
$m^d /m^{d+1}\subset {\mathfrak g}$ provided that ![]() $2 \leq d < 2n(p-1)$. The base of induction,
$2 \leq d < 2n(p-1)$. The base of induction, ![]() $d = 3$, can be easily checked directly follows from Lemma A.6.
$d = 3$, can be easily checked directly follows from Lemma A.6.
Choose a symplectic basis ![]() $(x_i, y_j)$ for
$(x_i, y_j)$ for ![]() $V^*$ and let
$V^*$ and let ![]() $E = x_1^{a_1}y_1^{b_1}\ldots x_n^{a_n}y_n^{b_n} \in m^d / m^{d+1}$ with
$E = x_1^{a_1}y_1^{b_1}\ldots x_n^{a_n}y_n^{b_n} \in m^d / m^{d+1}$ with ![]() $d > 3$.
$d > 3$.
Note that:
•
 $3a_ix_1^{a_i}y_i^{b_i} =\{x_i^{a_i+1}y_1^{b_i-2}, y_i^3\}$ (and
$3a_ix_1^{a_i}y_i^{b_i} =\{x_i^{a_i+1}y_1^{b_i-2}, y_i^3\}$ (and  $-3b_ix_1^{a_i}y_1^{b_i} =\{x_i^{a_i-2}y_1^{b_i+1}, y_1^3\}$);
$-3b_ix_1^{a_i}y_1^{b_i} =\{x_i^{a_i-2}y_1^{b_i+1}, y_1^3\}$);•
 $(a-1-2b)x_i^{a}y_i^b = \{ x_i^{a-1}y_i^b, x_i^2y_i\}$ (and
$(a-1-2b)x_i^{a}y_i^b = \{ x_i^{a-1}y_i^b, x_i^2y_i\}$ (and  $(2a - b + 1)x_i^{a}y_i^b = \{ x_i^{a}y_i^{b-1}, x_iy_i^2\}$);
$(2a - b + 1)x_i^{a}y_i^b = \{ x_i^{a}y_i^{b-1}, x_iy_i^2\}$);•
 $- x_ix_j = \{x_iy_i, x_ix_j\}$;
$- x_ix_j = \{x_iy_i, x_ix_j\}$;•
 $x_i^{p-1}y_i^{p-1} + 2(p-1)x_i^{p-2}y_i^{p-2}x_jy_j= \{ x_i^{p-1}y_i^{p-3}x_j, y_i^2y_j\}$;
$x_i^{p-1}y_i^{p-1} + 2(p-1)x_i^{p-2}y_i^{p-2}x_jy_j= \{ x_i^{p-1}y_i^{p-3}x_j, y_i^2y_j\}$;•
 $2(p-1)x_i^{p-2}y_i^{p-2}x_j^2y_j + 2x_i^{p-1}y_i^{p-1}x_j=\{x_i^{p-1}y_i^{p-3}x_j^2, y_i^2y_j\}$.
$2(p-1)x_i^{p-2}y_i^{p-2}x_j^2y_j + 2x_i^{p-1}y_i^{p-1}x_j=\{x_i^{p-1}y_i^{p-3}x_j^2, y_i^2y_j\}$.
Assume first that ![]() $p > 3$. Then if for some
$p > 3$. Then if for some ![]() $i$ we have
$i$ we have ![]() $a_i < p-1$ and
$a_i < p-1$ and ![]() $b_i \geq 2$ (or
$b_i \geq 2$ (or ![]() $a_i \geq 2$ and
$a_i \geq 2$ and ![]() $b_i < p-1$), then by the first formula above
$b_i < p-1$), then by the first formula above ![]() $E$ is generated by elements of degree
$E$ is generated by elements of degree ![]() $2 \leq d^{\prime } < d$, which are in
$2 \leq d^{\prime } < d$, which are in ![]() ${\mathfrak g}$ by the induction assumption. Otherwise, for all
${\mathfrak g}$ by the induction assumption. Otherwise, for all ![]() $i$ the pair
$i$ the pair ![]() $(a_i, b_i)$ equals
$(a_i, b_i)$ equals ![]() $(p-1, p-1)$,
$(p-1, p-1)$, ![]() $(1, 1)$,
$(1, 1)$, ![]() $(1, 0)$, or
$(1, 0)$, or ![]() $(0,1)$.
$(0,1)$.
If for some ![]() $i$ the pair is
$i$ the pair is ![]() $(1, 1)$ we get that from the second formula that
$(1, 1)$ we get that from the second formula that ![]() $E \in {\mathfrak g}$. If there are at least two pairs of the type
$E \in {\mathfrak g}$. If there are at least two pairs of the type ![]() $(1, 0)$ or
$(1, 0)$ or ![]() $(0,1)$ we are done by the third formula.
$(0,1)$ we are done by the third formula.
Otherwise we may assume that ![]() $E = x_1^{p-1}y_1^{p-1} \ldots x_{n-r}^{p-1}y_{n-r}^{p-1}$ or
$E = x_1^{p-1}y_1^{p-1} \ldots x_{n-r}^{p-1}y_{n-r}^{p-1}$ or ![]() $E = x_1^{p-1}y_1^{p-1} \ldots x_{n-r}^{p-1}y_{n-r}^{p-1}x_{n - r + 1}$ for some
$E = x_1^{p-1}y_1^{p-1} \ldots x_{n-r}^{p-1}y_{n-r}^{p-1}x_{n - r + 1}$ for some ![]() $0 < r < n$. In these cases we are done by the last two formulas.
$0 < r < n$. In these cases we are done by the last two formulas.
Now assume ![]() $p = 3$. For
$p = 3$. For ![]() $d>3$ note that if for some
$d>3$ note that if for some ![]() $i$ the number
$i$ the number ![]() $a_i + b_i - 1$ is not divisible by 3 we are done using the second formula. Thus, assume that for all
$a_i + b_i - 1$ is not divisible by 3 we are done using the second formula. Thus, assume that for all ![]() $i$ the pair
$i$ the pair ![]() $(a_i, b_i)$ equals either
$(a_i, b_i)$ equals either ![]() $(p-1, p-1)$,
$(p-1, p-1)$, ![]() $(1, 1)$,
$(1, 1)$, ![]() $(1, 0)$ or
$(1, 0)$ or ![]() $(0, 1)$. In these cases we proceed as above.
$(0, 1)$. In these cases we proceed as above.
Lemma 4.4 We have the following commutative diagram.

Moreover, the projection ![]() $G_0 \to G_0 / [G_0, G_0]$ admits a section yielding to a decomposition
$G_0 \to G_0 / [G_0, G_0]$ admits a section yielding to a decomposition ![]() $G_0 \cong [G_0, G_0] \rtimes \mathbb {G}_a$. Lastly, we have that
$G_0 \cong [G_0, G_0] \rtimes \mathbb {G}_a$. Lastly, we have that
Proof. Let us construct a group scheme homomorphism ![]() $\phi$ from
$\phi$ from ![]() $G_0$ to
$G_0$ to ![]() $\mathbb {G}_a$. For a
$\mathbb {G}_a$. For a ![]() $k$-algebra
$k$-algebra ![]() $R$ and
$R$ and ![]() $g \in G_0(R)$, we have that
$g \in G_0(R)$, we have that ![]() $g(\eta ) = \eta + df \in \Omega ^1_{A_0\otimes R/R}$, for some
$g(\eta ) = \eta + df \in \Omega ^1_{A_0\otimes R/R}$, for some ![]() $f \in \operatorname {coker} (R \to A_0 \otimes R)$. Consider the element
$f \in \operatorname {coker} (R \to A_0 \otimes R)$. Consider the element
where the isomorphism above is induced by ![]() $k \buildrel {\sim }\over {\longrightarrow } H_{{\rm DR}}^{2n}(A_0)$ that takes
$k \buildrel {\sim }\over {\longrightarrow } H_{{\rm DR}}^{2n}(A_0)$ that takes ![]() $1\in k$ to the inverse Cartier operator applied to
$1\in k$ to the inverse Cartier operator applied to ![]() $\omega ^n$.
$\omega ^n$.
To show that ![]() $\phi$ is a homomorphism consider two elements
$\phi$ is a homomorphism consider two elements ![]() $g_1, g_2 \in G_0(R)$. Write
$g_1, g_2 \in G_0(R)$. Write ![]() $g_1(\eta ) = \eta + df_1, g_2(\eta ) = \eta + df_2$. Since
$g_1(\eta ) = \eta + df_1, g_2(\eta ) = \eta + df_2$. Since ![]() $g_2 \circ g_1(\eta ) = \eta + df_2 + d(g_2(f_1))$ the image of
$g_2 \circ g_1(\eta ) = \eta + df_2 + d(g_2(f_1))$ the image of ![]() $g_2 \circ g_1$ equals
$g_2 \circ g_1$ equals ![]() $[(f_2 + g_2(f_1)) \cdot (\omega )^n]$. On the other hand,
$[(f_2 + g_2(f_1)) \cdot (\omega )^n]$. On the other hand, ![]() $\phi (g_1) + \phi (g_2) = [(f_2 + f_1) \cdot (\omega )^n]$. Thus, it suffices to prove that
$\phi (g_1) + \phi (g_2) = [(f_2 + f_1) \cdot (\omega )^n]$. Thus, it suffices to prove that ![]() $G_0$ acts trivially on
$G_0$ acts trivially on ![]() $H_{{\rm DR}}^{2n}(A_0)$. We claim that, in fact, every
$H_{{\rm DR}}^{2n}(A_0)$. We claim that, in fact, every ![]() $1$-dimensional representation of
$1$-dimensional representation of ![]() $G_0$ is trivial. Indeed,
$G_0$ is trivial. Indeed, ![]() $G_0$ is generated by two subgroups
$G_0$ is generated by two subgroups ![]() $\alpha =\alpha _p^{2n}$ and
$\alpha =\alpha _p^{2n}$ and ![]() $G_0^0$. Since
$G_0^0$. Since ![]() $\alpha$ has no nontrivial homomorphisms to
$\alpha$ has no nontrivial homomorphisms to ![]() $\mathbb {G}_m$ it suffices to prove the assertion for
$\mathbb {G}_m$ it suffices to prove the assertion for ![]() $G_0^0$. By Lemma 4.1
$G_0^0$. By Lemma 4.1 ![]() $G_0^0$ is an extension of
$G_0^0$ is an extension of ![]() $\operatorname {Sp}(2n)$ by a unipotent group and neither of the two groups has nontrivial
$\operatorname {Sp}(2n)$ by a unipotent group and neither of the two groups has nontrivial ![]() $1$-dimensional representations. This proves that
$1$-dimensional representations. This proves that ![]() $\phi$ is homomorphism.
$\phi$ is homomorphism.
The restriction of ![]() $\phi$ to
$\phi$ to ![]() $G_0^0$ yields a homomorphism
$G_0^0$ yields a homomorphism
Next, we shall construct a homomorphism ![]() $s: \mathbb {G}_a = \operatorname {Spec} k[t] \to G_0^0$ whose composition with the projection
$s: \mathbb {G}_a = \operatorname {Spec} k[t] \to G_0^0$ whose composition with the projection ![]() $G_0^0 \to G_0^0 / [G_0^0, G_0^0]$ followed by (4.6) is
$G_0^0 \to G_0^0 / [G_0^0, G_0^0]$ followed by (4.6) is ![]() $\operatorname {Id}$. Set
$\operatorname {Id}$. Set ![]() $u = \prod x_i^{p-1} \prod y_i^{p-1} \in A_0$. Define
$u = \prod x_i^{p-1} \prod y_i^{p-1} \in A_0$. Define ![]() $s(t) \in Aut_{k[t]} (A_0[t])$ sending
$s(t) \in Aut_{k[t]} (A_0[t])$ sending ![]() $f \in A_0$ to
$f \in A_0$ to ![]() $f- ({t}/{2}) \{f,u\}$. One verifies directly that
$f- ({t}/{2}) \{f,u\}$. One verifies directly that ![]() $s$ is group homomorphism and a section of (4.6). Let us check that (4.6) is an isomorphism. First, from Lemma 4.3 we know that
$s$ is group homomorphism and a section of (4.6). Let us check that (4.6) is an isomorphism. First, from Lemma 4.3 we know that ![]() $[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$ has codimension
$[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$ has codimension ![]() $1$ in
$1$ in ![]() $\operatorname {Lie} G_0^0$. Second, since
$\operatorname {Lie} G_0^0$. Second, since ![]() $G^0_0=(G_0)_{\rm red}$ is smooth, both groups
$G^0_0=(G_0)_{\rm red}$ is smooth, both groups ![]() $[G_0^0, G_0^0]$ and
$[G_0^0, G_0^0]$ and ![]() $G_0^0 / [G_0^0, G_0^0]$ are also smooth. Moreover, we have that
$G_0^0 / [G_0^0, G_0^0]$ are also smooth. Moreover, we have that ![]() $[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0] \subset \operatorname {Lie} [G_0^0, G_0^0]$ (see e.g. [Reference BorelBor91, Proposition 3.17]). It follows that the dimension of
$[\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0] \subset \operatorname {Lie} [G_0^0, G_0^0]$ (see e.g. [Reference BorelBor91, Proposition 3.17]). It follows that the dimension of ![]() $G_0^0 / [G_0^0, G_0^0]$ is at most
$G_0^0 / [G_0^0, G_0^0]$ is at most ![]() $1$. Thus, (4.6) is a homomorphism from a smooth connected algebraic group of dimension
$1$. Thus, (4.6) is a homomorphism from a smooth connected algebraic group of dimension ![]() $\leq 1$ to
$\leq 1$ to ![]() $\mathbb {G}_a$ and as we have already seen this homomorphism admits a section. It follows that (4.6) is an isomorphism. This also proves formula (4.5).
$\mathbb {G}_a$ and as we have already seen this homomorphism admits a section. It follows that (4.6) is an isomorphism. This also proves formula (4.5).
To complete the proof of lemma it suffices to check that the homomorphism ![]() $G_0^0 / [G_0^0, G_0^0] \to G_0 / [G_0, G_0]$ is surjective. Since
$G_0^0 / [G_0^0, G_0^0] \to G_0 / [G_0, G_0]$ is surjective. Since ![]() $G_0$ is generated by
$G_0$ is generated by ![]() $\alpha$ and
$\alpha$ and ![]() $G^0_0$ it is enough to show that
$G^0_0$ it is enough to show that ![]() $\alpha \in [G_0, G_0]$. Consider the subgroup
$\alpha \in [G_0, G_0]$. Consider the subgroup ![]() $P= \alpha \rtimes \operatorname {Sp}(2n) \subset G_0$. We claim that
$P= \alpha \rtimes \operatorname {Sp}(2n) \subset G_0$. We claim that ![]() $[P,P]=P$. Indeed, there is a surjection
$[P,P]=P$. Indeed, there is a surjection ![]() $[P, P] \twoheadrightarrow [\operatorname {Sp}(2n), \operatorname {Sp}(2n) ] = \operatorname {Sp}(2n)$. The kernel of the surjection is a subgroup of
$[P, P] \twoheadrightarrow [\operatorname {Sp}(2n), \operatorname {Sp}(2n) ] = \operatorname {Sp}(2n)$. The kernel of the surjection is a subgroup of ![]() $\alpha$ whose Lie algebra is a
$\alpha$ whose Lie algebra is a ![]() $\operatorname {Sp}(2n)$-invariant subspace of
$\operatorname {Sp}(2n)$-invariant subspace of ![]() $\operatorname {Lie} \alpha$. It follows that the kernel is either trivial which clearly not the case or equal to
$\operatorname {Lie} \alpha$. It follows that the kernel is either trivial which clearly not the case or equal to ![]() $\alpha$ as desired.
$\alpha$ as desired.
Next, we shall show that ![]() $[G_0, G_0]$ is generated by
$[G_0, G_0]$ is generated by ![]() $\operatorname {Sp}(2n)$,
$\operatorname {Sp}(2n)$, ![]() $\alpha$, and a certain one-parameter subgroup
$\alpha$, and a certain one-parameter subgroup ![]() ${\mathbb {G}}_a \subset G_0^0$. We start with the following observation.
${\mathbb {G}}_a \subset G_0^0$. We start with the following observation.
Lemma 4.5 Let ![]() $f\in A_h$ be an element of the restricted Weyl algebra such that
$f\in A_h$ be an element of the restricted Weyl algebra such that ![]() $f^{({p+1})/{2}}=0$. Consider the homomorphism
$f^{({p+1})/{2}}=0$. Consider the homomorphism
given by the formula
 \[ e^{{\tau f}/{h}}= \sum_{i=0}^{ ({p-1})/{2}} \frac{(\tau f)^i}{h^i i!}. \]
\[ e^{{\tau f}/{h}}= \sum_{i=0}^{ ({p-1})/{2}} \frac{(\tau f)^i}{h^i i!}. \]
Then the ![]() $p$th power of the operator
$p$th power of the operator ![]() $\operatorname {ad}_{{\tau f}/{h}} : A_h \hat {\otimes } k[\tau ] \to A_h \hat {\otimes } k[\tau ]$ is zero and
$\operatorname {ad}_{{\tau f}/{h}} : A_h \hat {\otimes } k[\tau ] \to A_h \hat {\otimes } k[\tau ]$ is zero and
 \begin{equation} \operatorname{Ad}_{e^{ {\tau f}/{h} } } = \sum_{i=0}^{ p-1} \frac{\operatorname{ad}_{\tau f}^i}{h^i i!} =:e^{\operatorname{ad}_{{\tau f}/{h}}}. \end{equation}
\begin{equation} \operatorname{Ad}_{e^{ {\tau f}/{h} } } = \sum_{i=0}^{ p-1} \frac{\operatorname{ad}_{\tau f}^i}{h^i i!} =:e^{\operatorname{ad}_{{\tau f}/{h}}}. \end{equation}
In particular, ![]() $e^{{\tau f}/{h}}$ normalizes the lattice
$e^{{\tau f}/{h}}$ normalizes the lattice ![]() $\underline {A_h} \subset \underline {A_h(h^{-1})}$ and, thus, defines a homomorphism
$\underline {A_h} \subset \underline {A_h(h^{-1})}$ and, thus, defines a homomorphism
Proof. The only assertion that requires a proof is formula (4.7). Both sides of the equation can be thought as homomorphisms from ![]() ${\mathbb {G}}_a$ to the loop group of
${\mathbb {G}}_a$ to the loop group of ![]() $k((h))$-linear automorphisms of
$k((h))$-linear automorphisms of ![]() $A_h(h^{-1})$. One readily sees that the differentials of these homomorphisms at
$A_h(h^{-1})$. One readily sees that the differentials of these homomorphisms at ![]() $\tau =0$ are equal. It follows that the homomorphisms are equal on the subscheme
$\tau =0$ are equal. It follows that the homomorphisms are equal on the subscheme ![]() $\alpha _p \subset {\mathbb {G}}_a$. Also, by the assumption on
$\alpha _p \subset {\mathbb {G}}_a$. Also, by the assumption on ![]() $f$, both homomorphisms are given by matrices in
$f$, both homomorphisms are given by matrices in ![]() $\operatorname {End}_{k[\tau ]((h))}( A_h \hat {\otimes } k[\tau ] (h^{-1}))$ whose entries are polynomials in
$\operatorname {End}_{k[\tau ]((h))}( A_h \hat {\otimes } k[\tau ] (h^{-1}))$ whose entries are polynomials in ![]() $\tau$ of degree less than
$\tau$ of degree less than ![]() $p$. Therefore, the homomorphisms are equal on
$p$. Therefore, the homomorphisms are equal on ![]() ${\mathbb {G}}_a$.
${\mathbb {G}}_a$.
Let ![]() $(x_i, y_j)$ be a symplectic basis for
$(x_i, y_j)$ be a symplectic basis for ![]() $V^*$. For
$V^*$. For ![]() $p>3$, define a homomorphism
$p>3$, define a homomorphism
by the equations
The differential of ![]() $\lambda$ is the Hamiltonian vector field
$\lambda$ is the Hamiltonian vector field ![]() $H_{-x_1^3}$. The construction from Lemma 4.5 gives a lifting
$H_{-x_1^3}$. The construction from Lemma 4.5 gives a lifting ![]() $\tilde {\lambda }_{x_1^3}= e^{{\tau x_1^3}/{h}}: {\mathbb {G}}_a \to \widetilde {G}$ of
$\tilde {\lambda }_{x_1^3}= e^{{\tau x_1^3}/{h}}: {\mathbb {G}}_a \to \widetilde {G}$ of ![]() $\lambda$.
$\lambda$.
For ![]() $p = 3$ define
$p = 3$ define ![]() $\lambda$ by
$\lambda$ by
The differential of ![]() $\lambda$ in this case is
$\lambda$ in this case is ![]() $H_{-x_1^2y_1}$. The homomorphism
$H_{-x_1^2y_1}$. The homomorphism ![]() $\tilde {\lambda }_{x_1^3}= e^{{\tau x_1^2y_1}/{h}}: {\mathbb {G}}_a \to \tilde {G}$ lifts
$\tilde {\lambda }_{x_1^3}= e^{{\tau x_1^2y_1}/{h}}: {\mathbb {G}}_a \to \tilde {G}$ lifts ![]() $\lambda$.
$\lambda$.
Lemma 4.6 The group scheme ![]() $H: = [G_0, G_0]$ is generated by
$H: = [G_0, G_0]$ is generated by ![]() $\operatorname {Sp}(2n)$,
$\operatorname {Sp}(2n)$, ![]() $\alpha$, and the image of
$\alpha$, and the image of ![]() $\lambda$.
$\lambda$.
Proof. First, we show that ![]() $\alpha$ and
$\alpha$ and ![]() $[G_0^0, G_0^0]$ generate
$[G_0^0, G_0^0]$ generate ![]() $H$. Indeed, since
$H$. Indeed, since ![]() $\alpha \subset H$, we have that, for any
$\alpha \subset H$, we have that, for any ![]() $k$-algebra
$k$-algebra ![]() $R$
$R$
Thus, it suffices to prove that ![]() $G_0^0(R) \cap H(R) = [G_0^0, G_0^0](R)$. By Lemma 4.4
$G_0^0(R) \cap H(R) = [G_0^0, G_0^0](R)$. By Lemma 4.4 ![]() $G_0^0 / [G_0^0, G_0^0] \cong G_0 / H$, so the assertion holds.
$G_0^0 / [G_0^0, G_0^0] \cong G_0 / H$, so the assertion holds.
Thus, it remains to prove that ![]() $[G_0^0, G_0^0]$ is generated by
$[G_0^0, G_0^0]$ is generated by ![]() $\operatorname {Sp}(2n)$ and the image of
$\operatorname {Sp}(2n)$ and the image of ![]() $\lambda$. Since the groups in question are smooth it suffices to verify that
$\lambda$. Since the groups in question are smooth it suffices to verify that ![]() $\operatorname {Lie} [G_0^0, G_0^0]$ is generated by
$\operatorname {Lie} [G_0^0, G_0^0]$ is generated by ![]() $\operatorname {\mathfrak {sp}}(2n)$ and
$\operatorname {\mathfrak {sp}}(2n)$ and ![]() $\operatorname {Lie} \lambda ({\mathbb {G}}_a)$. But this is immediate from Lemmas 4.3 and 4.4.
$\operatorname {Lie} \lambda ({\mathbb {G}}_a)$. But this is immediate from Lemmas 4.3 and 4.4.
Consider the extension
from Lemma 4.2.
Lemma 4.7 The restriction of the extension (4.10) to ![]() $G_0^0$ admits a unique splitting, that is, there exists a unique homomorphism
$G_0^0$ admits a unique splitting, that is, there exists a unique homomorphism ![]() $G_0^0 \to \widetilde G^e_0$ whose composition with the projection
$G_0^0 \to \widetilde G^e_0$ whose composition with the projection ![]() $\widetilde G^e_0 \to G_0$ is the identity.
$\widetilde G^e_0 \to G_0$ is the identity.
Proof. Recall from (3.6) the extension
The kernel ![]() $\underline {A}_h ^*/{\mathbb {G}}_m$ of surjection
$\underline {A}_h ^*/{\mathbb {G}}_m$ of surjection ![]() $\pi : G \to G_0$ is a pro-unipotent group scheme. Thus, by part (iii) of Proposition A.5 the restriction of the above extension to
$\pi : G \to G_0$ is a pro-unipotent group scheme. Thus, by part (iii) of Proposition A.5 the restriction of the above extension to ![]() $\pi ^{-1}G_0^0\hookrightarrow G$ admits a unique reduction to
$\pi ^{-1}G_0^0\hookrightarrow G$ admits a unique reduction to ![]() $L^+ {\mathbb {G}}_m$. Equivalently, the extension
$L^+ {\mathbb {G}}_m$. Equivalently, the extension
admits a unique splitting ![]() $\upsilon : G^0_0 \to \tilde {G}_0$ over
$\upsilon : G^0_0 \to \tilde {G}_0$ over ![]() $G^0_0\subset G_0$. It remains to show that
$G^0_0\subset G_0$. It remains to show that ![]() $\upsilon$ lands in
$\upsilon$ lands in ![]() $\widetilde G^e_0$. From the proof of Lemma 4.2
$\widetilde G^e_0$. From the proof of Lemma 4.2 ![]() $\widetilde G^e_0$ is the kernel of a homomorphism
$\widetilde G^e_0$ is the kernel of a homomorphism ![]() $\widetilde {G}_0 \to \underline {\mathbb {Z}}$. Since
$\widetilde {G}_0 \to \underline {\mathbb {Z}}$. Since ![]() $G^0_0$ is connected its composition with
$G^0_0$ is connected its composition with ![]() $\upsilon$ is identically
$\upsilon$ is identically ![]() $0$ as desired.
$0$ as desired.
Recall from Remark 3.2 an isomorphism of Lie algebras ![]() $\operatorname {Lie} \widetilde G^e_0 = \operatorname {Lie} \widetilde G_0 \buildrel {\sim }\over {\longrightarrow } A_0 \oplus h^{-2} k[h^{-1} ]$. Also recall an identification
$\operatorname {Lie} \widetilde G^e_0 = \operatorname {Lie} \widetilde G_0 \buildrel {\sim }\over {\longrightarrow } A_0 \oplus h^{-2} k[h^{-1} ]$. Also recall an identification ![]() $\operatorname {Lie} G_0^0\buildrel {\sim }\over {\longrightarrow } m^2\subset A_0$.
$\operatorname {Lie} G_0^0\buildrel {\sim }\over {\longrightarrow } m^2\subset A_0$.
Lemma 4.8 The morphism ![]() $\operatorname {Lie} G_0^0 \to \operatorname {Lie} \widetilde G^e_0$ induced by the splitting from Lemma 4.7 equals the composition
$\operatorname {Lie} G_0^0 \to \operatorname {Lie} \widetilde G^e_0$ induced by the splitting from Lemma 4.7 equals the composition ![]() $m^2 \hookrightarrow A_0 \hookrightarrow \operatorname {Lie} \widetilde G^e_0$.
$m^2 \hookrightarrow A_0 \hookrightarrow \operatorname {Lie} \widetilde G^e_0$.
Proof. The difference of the two morphisms of Lie algebras is a homomorphism from ![]() $\operatorname {Lie} G_0^0$ to the abelian Lie algebra
$\operatorname {Lie} G_0^0$ to the abelian Lie algebra ![]() $\operatorname {Lie} \hat {{\mathbb {W}}}$. Thus, it suffices to check that the morphisms coincide on the one-dimensional Lie algebra
$\operatorname {Lie} \hat {{\mathbb {W}}}$. Thus, it suffices to check that the morphisms coincide on the one-dimensional Lie algebra ![]() $\operatorname {Lie} G_0^0 / [\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$, which is immediate from Lemma 4.4.
$\operatorname {Lie} G_0^0 / [\operatorname {Lie} G_0^0, \operatorname {Lie} G_0^0]$, which is immediate from Lemma 4.4.
4.2 Extensions of  $\alpha$ by
$\alpha$ by  $\hat {{\mathbb {W}}}$
$\hat {{\mathbb {W}}}$
In this subsection we shall apply the theory of restricted Lie algebras to study the category of central extensions of the group scheme ![]() $\alpha$ by the group ind-scheme
$\alpha$ by the group ind-scheme ![]() $\hat {{\mathbb {W}}}$. Recall (see e.g. [Reference Demazure and GabrielDG80, Chapter II, § 7]) that the Lie algebra of a group scheme
$\hat {{\mathbb {W}}}$. Recall (see e.g. [Reference Demazure and GabrielDG80, Chapter II, § 7]) that the Lie algebra of a group scheme ![]() $H$ over a field of characteristic
$H$ over a field of characteristic ![]() $p>0$ is equipped with the
$p>0$ is equipped with the ![]() $p$th power operation giving
$p$th power operation giving ![]() $\operatorname {Lie} H$ a restricted Lie algebra structure. We are not aware of a written account of such theory for group ind-schemes. Therefore, we shall use the following trick to reduce our problem to the well documented setup.
$\operatorname {Lie} H$ a restricted Lie algebra structure. We are not aware of a written account of such theory for group ind-schemes. Therefore, we shall use the following trick to reduce our problem to the well documented setup.
For an affine scheme ![]() $S$ and an affine group scheme
$S$ and an affine group scheme ![]() $H$ over
$H$ over ![]() $k$ denote by
$k$ denote by ![]() $\underline {\operatorname {Mor}}(S, H)$ the fpqc sheaf of groups assigning to a scheme
$\underline {\operatorname {Mor}}(S, H)$ the fpqc sheaf of groups assigning to a scheme ![]() $T$ over
$T$ over ![]() $k$ the group
$k$ the group ![]() $\operatorname {Mor}(S\times T, H)$.
$\operatorname {Mor}(S\times T, H)$.
Lemma 4.9 Let ![]() $G$ be a finite connected group scheme over
$G$ be a finite connected group scheme over ![]() $k$,
$k$, ![]() $H$ a smooth commutative group scheme, and let
$H$ a smooth commutative group scheme, and let ![]() $S$ be an affine scheme. Then the groupoid of central extensions of
$S$ be an affine scheme. Then the groupoid of central extensions of ![]() $G$ by
$G$ by ![]() $\underline {\operatorname {Mor}}(S, H)$ in the category of fpqc sheaves of groups is equivalent to the category of central extensions of
$\underline {\operatorname {Mor}}(S, H)$ in the category of fpqc sheaves of groups is equivalent to the category of central extensions of ![]() $G_S = G \times S$ by
$G_S = G \times S$ by ![]() $H_S= H\times S$ in the category of group schemes over
$H_S= H\times S$ in the category of group schemes over ![]() $S$.
$S$.
Proof. Assume we are given a central extension
and let us construct a central extension ![]() $F$ of
$F$ of ![]() $G$ by
$G$ by ![]() $\underline {\operatorname {Mor}}(S, H)$. For any scheme
$\underline {\operatorname {Mor}}(S, H)$. For any scheme ![]() $T$ over
$T$ over ![]() $\operatorname {Spec}(k)$ define
$\operatorname {Spec}(k)$ define ![]() $F(T) = \{g \in K(T \times S) | T \times S \stackrel {\pi (g)}{\longrightarrow } G \times S \rightarrow G \text { factors through the projection to } T\}$. It is easy to see that the resulting
$F(T) = \{g \in K(T \times S) | T \times S \stackrel {\pi (g)}{\longrightarrow } G \times S \rightarrow G \text { factors through the projection to } T\}$. It is easy to see that the resulting ![]() $F$ is a sheaf and that
$F$ is a sheaf and that ![]() $\underline {\operatorname {Mor}}(S, H)$ injects into it, so it is left to prove that
$\underline {\operatorname {Mor}}(S, H)$ injects into it, so it is left to prove that ![]() $F \rightarrow G$ is a surjection. Indeed, since the morphism
$F \rightarrow G$ is a surjection. Indeed, since the morphism ![]() $\pi$ is flat and
$\pi$ is flat and ![]() $H_S$ is smooth we get that
$H_S$ is smooth we get that ![]() $K \rightarrow G_S$ is formally smooth [Sta, Lemma 29.33.3]. Then since the map
$K \rightarrow G_S$ is formally smooth [Sta, Lemma 29.33.3]. Then since the map ![]() $\operatorname {Spec}(k) \times S \rightarrow G \times S$ is a nilpotent thickening we get that
$\operatorname {Spec}(k) \times S \rightarrow G \times S$ is a nilpotent thickening we get that ![]() $\pi$ has a section. Thus,
$\pi$ has a section. Thus, ![]() $F \rightarrow G$ is surjective.
$F \rightarrow G$ is surjective.
Conversely, if we have a central extension
define for any ![]() $S$-scheme
$S$-scheme ![]() $T$ the group
$T$ the group ![]() $K(T)$ to be
$K(T)$ to be ![]() $F(T) \times ^{\operatorname {Mor}(T \times S, H)} \operatorname {Mor}(T, H)$. Here the map
$F(T) \times ^{\operatorname {Mor}(T \times S, H)} \operatorname {Mor}(T, H)$. Here the map ![]() $\operatorname {Mor}(T \times S, H) \rightarrow F(T)$ is induced by
$\operatorname {Mor}(T \times S, H) \rightarrow F(T)$ is induced by ![]() $i$ and
$i$ and ![]() $Mor(T \times S, H) \rightarrow \operatorname {Mor}(T, H)$ is defined to be the restriction to the graph of the structure morphism
$Mor(T \times S, H) \rightarrow \operatorname {Mor}(T, H)$ is defined to be the restriction to the graph of the structure morphism ![]() $T \to S$. Let
$T \to S$. Let ![]() $H_S(T) \rightarrow F(T) \times \operatorname {Mor}(T, H)$ be the homomorphism whose composition with the first projection takes
$H_S(T) \rightarrow F(T) \times \operatorname {Mor}(T, H)$ be the homomorphism whose composition with the first projection takes ![]() $H_S(T)$ to the neutral element and whose composition with the second projection is the identity map. This defines an injection of sheaves
$H_S(T)$ to the neutral element and whose composition with the second projection is the identity map. This defines an injection of sheaves ![]() $H_S \hookrightarrow K$, making
$H_S \hookrightarrow K$, making ![]() $K$ into an
$K$ into an ![]() $H_S$-torsor over
$H_S$-torsor over ![]() $G_S$ representable by a scheme [Reference MilneMil80, Chapter III, Theorem 4.3]. That is enough.
$G_S$ representable by a scheme [Reference MilneMil80, Chapter III, Theorem 4.3]. That is enough.
Corollary 4.10 The groupoid of central extensions of ![]() $\alpha$ by
$\alpha$ by ![]() $\underline {\operatorname {Mor}}(\mathbb {A}^1, \mathbb {G}_m)$ in the category of fpqc sheaves is equivalent to the groupoid of central extensions of
$\underline {\operatorname {Mor}}(\mathbb {A}^1, \mathbb {G}_m)$ in the category of fpqc sheaves is equivalent to the groupoid of central extensions of ![]() $\alpha \times \mathbb {A}^1$ by
$\alpha \times \mathbb {A}^1$ by ![]() $\mathbb {G}_m \times \mathbb {A}^1$ in the category of group schemes over
$\mathbb {G}_m \times \mathbb {A}^1$ in the category of group schemes over ![]() $\mathbb {A}^1$.
$\mathbb {A}^1$.
Remark 4.11 The above groupoids are discrete, i.e. objects do not have nontrivial automorphisms. Indeed, the Cartier dual group to ![]() $\alpha$ is isomorphic to itself. In particular, it has no nontrivial
$\alpha$ is isomorphic to itself. In particular, it has no nontrivial ![]() $\mathbb {A}^1$ points. Hence, every homomorphism
$\mathbb {A}^1$ points. Hence, every homomorphism ![]() $\alpha \times \mathbb {A}^1 \to \mathbb {G}_m \times \mathbb {A}^1$ in the category of group schemes over
$\alpha \times \mathbb {A}^1 \to \mathbb {G}_m \times \mathbb {A}^1$ in the category of group schemes over ![]() $\mathbb {A}^1$ is trivial.
$\mathbb {A}^1$ is trivial.
Observe that the evaluation at ![]() $0$ defines a split surjection
$0$ defines a split surjection ![]() $\underline {\operatorname {Mor}}(\mathbb {A}^1, \mathbb {G}_m) \to \mathbb {G}_m$, whose kernel is identified with
$\underline {\operatorname {Mor}}(\mathbb {A}^1, \mathbb {G}_m) \to \mathbb {G}_m$, whose kernel is identified with ![]() $\hat {{\mathbb {W}}}$. Hence, we have a decomposition
$\hat {{\mathbb {W}}}$. Hence, we have a decomposition ![]() $\underline {\operatorname {Mor}}(\mathbb {A}^1, \mathbb {G}_m) = \hat {{\mathbb {W}}} \times \mathbb {G}_m$.
$\underline {\operatorname {Mor}}(\mathbb {A}^1, \mathbb {G}_m) = \hat {{\mathbb {W}}} \times \mathbb {G}_m$.
Declare the restricted Lie algebra of ![]() $\operatorname {Gr}_G$ to be
$\operatorname {Gr}_G$ to be ![]() $\operatorname {Lie}(\operatorname {Gr}_{G}^0) = h^{-1}k[h^{-1}]$ with the trivial Lie bracket and the restricted power operation given by the absolute Frobenius.
$\operatorname {Lie}(\operatorname {Gr}_{G}^0) = h^{-1}k[h^{-1}]$ with the trivial Lie bracket and the restricted power operation given by the absolute Frobenius.
Theorem 2 The groupoid of central extensions of the group scheme ![]() $\alpha$ by
$\alpha$ by ![]() $\hat {{\mathbb {W}}}$ is equivalent to the groupoid of central extensions of the restricted Lie algebra
$\hat {{\mathbb {W}}}$ is equivalent to the groupoid of central extensions of the restricted Lie algebra ![]() $\operatorname {Lie}(\alpha )$ by
$\operatorname {Lie}(\alpha )$ by ![]() $\operatorname {Lie}(\hat {{\mathbb {W}}})$.
$\operatorname {Lie}(\hat {{\mathbb {W}}})$.
Proof. Using that the multiplication by ![]() $p$ is
$p$ is ![]() $0$ on
$0$ on ![]() $\alpha$ and surjective on
$\alpha$ and surjective on ![]() $\hat {{\mathbb {W}}}$ it follows that every extension of
$\hat {{\mathbb {W}}}$ it follows that every extension of ![]() $\alpha$ by
$\alpha$ by ![]() $\hat {{\mathbb {W}}}$ admits a reduction to
$\hat {{\mathbb {W}}}$ admits a reduction to ![]() $\operatorname {Gr}^0_{\mu _p}$. Moreover, since
$\operatorname {Gr}^0_{\mu _p}$. Moreover, since ![]() $\operatorname {Hom} (\alpha, \hat {{\mathbb {W}}}) =0$ (by Corollary A.3), such a reduction is unique. Thus, the groupoid of central extensions of
$\operatorname {Hom} (\alpha, \hat {{\mathbb {W}}}) =0$ (by Corollary A.3), such a reduction is unique. Thus, the groupoid of central extensions of ![]() $\alpha$ by
$\alpha$ by ![]() $\hat {{\mathbb {W}}}$ is equivalent to the groupoid of central extensions of
$\hat {{\mathbb {W}}}$ is equivalent to the groupoid of central extensions of ![]() $\alpha$ by
$\alpha$ by ![]() $\operatorname {Gr}^0_{\mu _p}$. The groupoid of central extensions of
$\operatorname {Gr}^0_{\mu _p}$. The groupoid of central extensions of ![]() $\alpha$ by
$\alpha$ by ![]() $\operatorname {Gr}_{\mu _p}^0$ is equivalent to a full subcategory of the groupoid of central extensions of
$\operatorname {Gr}_{\mu _p}^0$ is equivalent to a full subcategory of the groupoid of central extensions of ![]() $\alpha \times \mathbb {A}^1$ by
$\alpha \times \mathbb {A}^1$ by ![]() $\mu _p \times \mathbb {A}^1$. This subcategory classifies families of central extensions whose fiber over
$\mu _p \times \mathbb {A}^1$. This subcategory classifies families of central extensions whose fiber over ![]() $0 \in \mathbb {A}^1$ is a trivial extension.
$0 \in \mathbb {A}^1$ is a trivial extension.
Next we claim that for an extension
the ![]() $\mathbb {A}^1$-group scheme is of height
$\mathbb {A}^1$-group scheme is of height ![]() $1$. Indeed, the Frobenius map
$1$. Indeed, the Frobenius map ![]() $K \to K$ factors as
$K \to K$ factors as ![]() $K \to \alpha \times \mathbb {A}^1 \to \mu _p \times \mathbb {A}^1 \to K$. From Remark 4.11 we conclude that this map is trivial.
$K \to \alpha \times \mathbb {A}^1 \to \mu _p \times \mathbb {A}^1 \to K$. From Remark 4.11 we conclude that this map is trivial.
Thus, by [Reference Demazure and GabrielDG80, Chapter II, § 7, Theorem 3.5] the category of central extensions of ![]() $\alpha \times \mathbb {A}^1$ by
$\alpha \times \mathbb {A}^1$ by ![]() $\mu _p \times \mathbb {A}^1$ is equivalent to the category of extensions of corresponding restricted Lie algebras over
$\mu _p \times \mathbb {A}^1$ is equivalent to the category of extensions of corresponding restricted Lie algebras over ![]() $\mathbb {A}^1$. The latter is equivalent to the category of extensions of
$\mathbb {A}^1$. The latter is equivalent to the category of extensions of ![]() $\operatorname {Lie}(\alpha )$ by
$\operatorname {Lie}(\alpha )$ by ![]() $\operatorname {Lie}(\mu _p \times \mathbb {A}^1)$ in the category of restricted Lie algebras over
$\operatorname {Lie}(\mu _p \times \mathbb {A}^1)$ in the category of restricted Lie algebras over ![]() $k$. The above equivalence induces an equivalence between the subcategories of central extensions of
$k$. The above equivalence induces an equivalence between the subcategories of central extensions of ![]() $\alpha \times \mathbb {A}^1$ by
$\alpha \times \mathbb {A}^1$ by ![]() $\mu _p \times \mathbb {A}^1$ trivial over
$\mu _p \times \mathbb {A}^1$ trivial over ![]() $0 \in \mathbb {A}^1$ and the category of restricted Lie algebra extensions of
$0 \in \mathbb {A}^1$ and the category of restricted Lie algebra extensions of ![]() $\operatorname {Lie}(\alpha )$ by
$\operatorname {Lie}(\alpha )$ by ![]() $\operatorname {Lie}(\hat {{\mathbb {W}}})$.
$\operatorname {Lie}(\hat {{\mathbb {W}}})$.
Corollary 4.12 The groupoid of central extensions of the group scheme ![]() $\alpha$ by
$\alpha$ by ![]() $\hat {{\mathbb {W}}}$ which split over any factor
$\hat {{\mathbb {W}}}$ which split over any factor ![]() $\alpha _{p} \subset \alpha$ is equivalent to the set of
$\alpha _{p} \subset \alpha$ is equivalent to the set of ![]() $\operatorname {Lie}(\hat {{\mathbb {W}}})$-valued skew-symmetric bilinear forms on
$\operatorname {Lie}(\hat {{\mathbb {W}}})$-valued skew-symmetric bilinear forms on ![]() $\operatorname {Lie}(\alpha )$ viewed as a groupoid with no nontrivial morphisms.
$\operatorname {Lie}(\alpha )$ viewed as a groupoid with no nontrivial morphisms.
Proof. Given a central extension of ![]() $\alpha$ by
$\alpha$ by ![]() $\hat {{\mathbb {W}}}$ let
$\hat {{\mathbb {W}}}$ let
be the corresponding extension of Lie algebras. The commutator on ![]() ${\mathcal {L}}$ defines a
${\mathcal {L}}$ defines a ![]() $\operatorname {Lie}(\hat {{\mathbb {W}}})$-valued skew-symmetric bilinear form on
$\operatorname {Lie}(\hat {{\mathbb {W}}})$-valued skew-symmetric bilinear form on ![]() $\operatorname {Lie}(\alpha )$. To construct the functor in the other direction set
$\operatorname {Lie}(\alpha )$. To construct the functor in the other direction set ![]() ${\mathcal {L}} = \operatorname {Lie}(\hat {{\mathbb {W}}}) \oplus \operatorname {Lie}(\alpha )$ as a vector space. The skew-symmetric form defines a Lie bracket on
${\mathcal {L}} = \operatorname {Lie}(\hat {{\mathbb {W}}}) \oplus \operatorname {Lie}(\alpha )$ as a vector space. The skew-symmetric form defines a Lie bracket on ![]() ${\mathcal {L}}$ making
${\mathcal {L}}$ making ![]() ${\mathcal {L}}$ a central extension of Lie algebras. Define the restricted power operation on
${\mathcal {L}}$ a central extension of Lie algebras. Define the restricted power operation on ![]() ${\mathcal {L}}$ by the formula
${\mathcal {L}}$ by the formula ![]() $(f, g)^{[p]} = f^{[p]}$. Let us check that
$(f, g)^{[p]} = f^{[p]}$. Let us check that ![]() ${\mathcal {L}}$ is a restricted Lie algebra. We have to check that the restricted power operation satisfies
${\mathcal {L}}$ is a restricted Lie algebra. We have to check that the restricted power operation satisfies
 \[ (X+Y)^{[p]}=X^{[p]}+Y^{[p]}+\sum_{i=1}^{p-1} \frac{s_{i}(X, Y)}{i} \]
\[ (X+Y)^{[p]}=X^{[p]}+Y^{[p]}+\sum_{i=1}^{p-1} \frac{s_{i}(X, Y)}{i} \]
for ![]() $X$ and
$X$ and ![]() $Y$ in the Lie algebra, and
$Y$ in the Lie algebra, and ![]() $s_{i}(X, Y)$ being the coefficient of
$s_{i}(X, Y)$ being the coefficient of ![]() $t^{i-1}$ in the formal expression
$t^{i-1}$ in the formal expression ![]() $\operatorname {ad}(t X+Y)^{p-1}(X)$. Since
$\operatorname {ad}(t X+Y)^{p-1}(X)$. Since ![]() $p > 2$ the polynomial
$p > 2$ the polynomial ![]() $s_{i}(X, Y) = 0$ for every
$s_{i}(X, Y) = 0$ for every ![]() $i$ as desired. It remains to check that every extension (4.14) of restricted Lie algebras that splits over every factor
$i$ as desired. It remains to check that every extension (4.14) of restricted Lie algebras that splits over every factor ![]() $\operatorname {Lie}(\alpha _p) \subset \operatorname {Lie}(\alpha )$ arises this way. As observed above, the restricted power operation on
$\operatorname {Lie}(\alpha _p) \subset \operatorname {Lie}(\alpha )$ arises this way. As observed above, the restricted power operation on ![]() ${\mathcal {L}}$ is additive. Now consider the subspace
${\mathcal {L}}$ is additive. Now consider the subspace ![]() $V$ of
$V$ of ![]() ${\mathcal {L}}$ consisting of elements annulated by
${\mathcal {L}}$ consisting of elements annulated by ![]() $[p]$-power operation. The projection defines an embedding
$[p]$-power operation. The projection defines an embedding ![]() $V \hookrightarrow \operatorname {Lie}(\alpha )$. Since the extension has a section over each
$V \hookrightarrow \operatorname {Lie}(\alpha )$. Since the extension has a section over each ![]() $\operatorname {Lie}(\alpha _p)$ the embedding is an isomorphism and we win.
$\operatorname {Lie}(\alpha _p)$ the embedding is an isomorphism and we win.
4.3 Geometric description of  $\widetilde G^e_0$
$\widetilde G^e_0$
Let
be the extension from Lemma 4.2, and let ![]() $\widetilde {\alpha }$ be its restriction to
$\widetilde {\alpha }$ be its restriction to ![]() $\alpha$.
$\alpha$.
Let us check that ![]() $\widetilde {\alpha }$ satisfies the assumptions of Corollary 4.12, that is splits over every subgroup
$\widetilde {\alpha }$ satisfies the assumptions of Corollary 4.12, that is splits over every subgroup ![]() $\alpha _p \subset \alpha$. For any
$\alpha _p \subset \alpha$. For any ![]() $v \in V$ set
$v \in V$ set ![]() $f = \omega _V(v, \cdot ) \in V^*$ and define a homomorphism
$f = \omega _V(v, \cdot ) \in V^*$ and define a homomorphism
Here ![]() $e^{ {\epsilon f}/{h}}$ denotes the restricted exponent, i.e.
$e^{ {\epsilon f}/{h}}$ denotes the restricted exponent, i.e. ![]() $e^{{\epsilon f}/{h}} = 1 + {\epsilon f}/{h} + \cdots + {1}/{(p-1)!}({\epsilon f}/{h})^{p-1}$. It is easy to see that
$e^{{\epsilon f}/{h}} = 1 + {\epsilon f}/{h} + \cdots + {1}/{(p-1)!}({\epsilon f}/{h})^{p-1}$. It is easy to see that ![]() $e^{{\epsilon f}/{h}} \in \underline {A_h [h^{-1}]^*}(\alpha _p)$ normalizes the lattice
$e^{{\epsilon f}/{h}} \in \underline {A_h [h^{-1}]^*}(\alpha _p)$ normalizes the lattice ![]() $A_h \otimes k[\epsilon ] / (\epsilon ^p)$; therefore, it lies in
$A_h \otimes k[\epsilon ] / (\epsilon ^p)$; therefore, it lies in ![]() $\widetilde {G}(\alpha _p)$. Then the composition of this homomorphism with the projection to
$\widetilde {G}(\alpha _p)$. Then the composition of this homomorphism with the projection to ![]() $\widetilde G_0$ is a lift of the embedding
$\widetilde G_0$ is a lift of the embedding ![]() $\alpha _p \subset \alpha$ corresponding to
$\alpha _p \subset \alpha$ corresponding to ![]() $v$ as desired.
$v$ as desired.
The natural action of ![]() $\operatorname {Sp}_{2n} \subset G_0^0 \subset G_0$ on
$\operatorname {Sp}_{2n} \subset G_0^0 \subset G_0$ on ![]() $\alpha$ by conjugation lifts to an action on
$\alpha$ by conjugation lifts to an action on ![]() $\widetilde {\alpha }$. Indeed, by Lemma 4.7 the extension (4.15) splits uniquely over
$\widetilde {\alpha }$. Indeed, by Lemma 4.7 the extension (4.15) splits uniquely over ![]() $\operatorname {Sp}_{2 n} \subset G_0^0$.
$\operatorname {Sp}_{2 n} \subset G_0^0$.
For future purposes note that the symplectic basis ![]() $(x_i, y_i)$ for
$(x_i, y_i)$ for ![]() $V^*$ gives rise to a scheme-theoretic section of
$V^*$ gives rise to a scheme-theoretic section of ![]() $\pi : \widetilde {\alpha } \to \alpha$. Namely,
$\pi : \widetilde {\alpha } \to \alpha$. Namely, ![]() $\alpha \cong \alpha _{p}^{2n}$, and we define
$\alpha \cong \alpha _{p}^{2n}$, and we define
by ![]() $e^{{\epsilon _1 x_1}/{h}} \ldots e^{{\epsilon _n x_n}/{h}} e^{{\delta _1 y_1}/{h}} \ldots e^{{\delta _n y_n}/{h}}$. The section
$e^{{\epsilon _1 x_1}/{h}} \ldots e^{{\epsilon _n x_n}/{h}} e^{{\delta _1 y_1}/{h}} \ldots e^{{\delta _n y_n}/{h}}$. The section ![]() $t$ is not a group homomorphism and it does depend on the choice of symplectic basis. However, its differential
$t$ is not a group homomorphism and it does depend on the choice of symplectic basis. However, its differential
is the unique linear map compatible with the restricted power operation.
Recall that a connection on a (trivial) ![]() $\hat {{\mathbb {W}}}$-torsor
$\hat {{\mathbb {W}}}$-torsor ![]() $\widetilde {\alpha }$ is a function
$\widetilde {\alpha }$ is a function
such that, for any ![]() $c \in \hat {{\mathbb {W}}}(\alpha )$, one has
$c \in \hat {{\mathbb {W}}}(\alpha )$, one has ![]() $\nabla (cs) = \nabla (s) + c^{-1}\,dc$. Denote by
$\nabla (cs) = \nabla (s) + c^{-1}\,dc$. Denote by ![]() $\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$ the set of
$\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$ the set of ![]() $\hat {{\mathbb {W}}}$-connections on
$\hat {{\mathbb {W}}}$-connections on ![]() $\widetilde {\alpha }$. More generally, we define the space
$\widetilde {\alpha }$. More generally, we define the space ![]() $\underline {\operatorname {Conn}}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$ of connections on
$\underline {\operatorname {Conn}}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$ of connections on ![]() $\widetilde {\alpha }$ to be the functor
$\widetilde {\alpha }$ to be the functor ![]() $(k-\text {algebras})^{\rm op}\to \text {Sets}$ sending an algebra
$(k-\text {algebras})^{\rm op}\to \text {Sets}$ sending an algebra ![]() $R$ to the set of functions
$R$ to the set of functions
with ![]() $\nabla (cs) = \nabla (s) + c^{-1}\,dc$, for every
$\nabla (cs) = \nabla (s) + c^{-1}\,dc$, for every ![]() $c\in {\mathbb {W}}( \alpha \times \operatorname {Spec} R )$. The group scheme
$c\in {\mathbb {W}}( \alpha \times \operatorname {Spec} R )$. The group scheme ![]() $S_{\alpha }$ of automorphisms of the scheme
$S_{\alpha }$ of automorphisms of the scheme ![]() $\alpha$ acts on the space
$\alpha$ acts on the space ![]() $\underline {\operatorname {Conn}}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$. In particular, for any subgroup
$\underline {\operatorname {Conn}}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$. In particular, for any subgroup ![]() $H\subset S_{\alpha }$, we have a subset
$H\subset S_{\alpha }$, we have a subset ![]() $\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})^{H}\subset \operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$ of
$\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})^{H}\subset \operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$ of ![]() $H$-invariant connections.
$H$-invariant connections.
Lemma 4.13 There exists a unique ![]() $\operatorname {Sp}_{2n} \ltimes \alpha$-invariant
$\operatorname {Sp}_{2n} \ltimes \alpha$-invariant ![]() $\hat {{\mathbb {W}}}$-connection
$\hat {{\mathbb {W}}}$-connection ![]() $\nabla$ on
$\nabla$ on ![]() $\widetilde {\alpha }$.
$\widetilde {\alpha }$.
Proof. Denote by ![]() $\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})^{\alpha }$ the set of
$\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})^{\alpha }$ the set of ![]() $\alpha$-invariant connections. We have that
$\alpha$-invariant connections. We have that
For an ![]() $\alpha$-invariant connection
$\alpha$-invariant connection ![]() $\nabla$, the corresponding
$\nabla$, the corresponding ![]() $f$ is given by the formula
$f$ is given by the formula
for any section ![]() $s$.
$s$.
Now since ![]() $\operatorname {Sp}_{2n}$ normalizes
$\operatorname {Sp}_{2n}$ normalizes ![]() $\alpha$ in
$\alpha$ in ![]() $G_0^0$ we get that
$G_0^0$ we get that ![]() $\operatorname {Sp}_{2n}$ acts on
$\operatorname {Sp}_{2n}$ acts on ![]() $\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})^{\alpha }$. Suppose we are given two
$\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})^{\alpha }$. Suppose we are given two ![]() $\operatorname {Sp}_{2n}$-invariant connections in
$\operatorname {Sp}_{2n}$-invariant connections in ![]() $\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})^{\alpha }$. Then their difference gives a morphism
$\operatorname {Conn}(\widetilde {\alpha }, \hat {{\mathbb {W}}})^{\alpha }$. Then their difference gives a morphism ![]() $\operatorname {Lie}(\alpha ) \rightarrow \operatorname {Lie}(\hat {{\mathbb {W}}})$ of representation of
$\operatorname {Lie}(\alpha ) \rightarrow \operatorname {Lie}(\hat {{\mathbb {W}}})$ of representation of ![]() $Sp_{2n}$, which has to be trivial since
$Sp_{2n}$, which has to be trivial since ![]() $\operatorname {Lie}(\alpha )$ is a nontrivial irreducible representation whereas the action of
$\operatorname {Lie}(\alpha )$ is a nontrivial irreducible representation whereas the action of ![]() $Sp_{2n}$ on
$Sp_{2n}$ on ![]() $\operatorname {Lie}(\hat {{\mathbb {W}}})$ is trivial. Thus, we get the uniqueness.
$\operatorname {Lie}(\hat {{\mathbb {W}}})$ is trivial. Thus, we get the uniqueness.
To prove the existence take (a unique) ![]() $f : \operatorname {Lie}(\tilde {\alpha }) \rightarrow \operatorname {Lie}(\hat {{\mathbb {W}}})$ that commutes with the restricted power operation (see the proof of Corollary 4.12). This morphism is
$f : \operatorname {Lie}(\tilde {\alpha }) \rightarrow \operatorname {Lie}(\hat {{\mathbb {W}}})$ that commutes with the restricted power operation (see the proof of Corollary 4.12). This morphism is ![]() $\operatorname {Sp}_{2n}$-invariant since the action of
$\operatorname {Sp}_{2n}$-invariant since the action of ![]() $\operatorname {Sp}_{2n}$ respects the restricted structure.
$\operatorname {Sp}_{2n}$ respects the restricted structure.
We will need an explicit formula for the ![]() $\operatorname {Sp}_{2n} \ltimes \alpha$-invariant connection
$\operatorname {Sp}_{2n} \ltimes \alpha$-invariant connection ![]() $\nabla$. Let
$\nabla$. Let ![]() $t$ be the section defined in (4.16). We claim that
$t$ be the section defined in (4.16). We claim that
To see this let us show that the connection given by (4.19) is ![]() $\operatorname {Sp}_{2n} \ltimes \alpha$-invariant. Pick a
$\operatorname {Sp}_{2n} \ltimes \alpha$-invariant. Pick a ![]() $k$-algebra
$k$-algebra ![]() $R$ and a point
$R$ and a point ![]() $a \in \alpha (R)$ given by
$a \in \alpha (R)$ given by ![]() $\epsilon _i \mapsto \epsilon _i^{\prime } \in R$. Then
$\epsilon _i \mapsto \epsilon _i^{\prime } \in R$. Then ![]() $t(a)$ is an
$t(a)$ is an ![]() $R$-point of
$R$-point of ![]() $\widetilde {\alpha }$ that acts on
$\widetilde {\alpha }$ that acts on ![]() $\widetilde {\alpha }$ by translation
$\widetilde {\alpha }$ by translation ![]() $\gamma$. The composition
$\gamma$. The composition ![]() $\gamma \circ t : \alpha \times \operatorname {Spec}(R) \to \widetilde {\alpha } \times \operatorname {Spec}(R)$ is given by the formula
$\gamma \circ t : \alpha \times \operatorname {Spec}(R) \to \widetilde {\alpha } \times \operatorname {Spec}(R)$ is given by the formula
Let ![]() $\bar {\gamma }$ be the translation by
$\bar {\gamma }$ be the translation by ![]() $a$ acting on
$a$ acting on ![]() $\alpha$. Then
$\alpha$. Then ![]() $t_{\gamma } = \gamma ^{-1}t\bar {\gamma }$ defines another section of
$t_{\gamma } = \gamma ^{-1}t\bar {\gamma }$ defines another section of ![]() $\pi$. The invariance of
$\pi$. The invariance of ![]() $\nabla$ under the action of
$\nabla$ under the action of ![]() $\gamma$ reads as
$\gamma$ reads as
Since ![]() $\bar {\gamma }(\epsilon _j) = \epsilon _j + \epsilon _j^{\prime }$ and
$\bar {\gamma }(\epsilon _j) = \epsilon _j + \epsilon _j^{\prime }$ and ![]() $\bar {\gamma }(\delta _j) = \delta _j + \delta _j^{\prime }$, we have that
$\bar {\gamma }(\delta _j) = \delta _j + \delta _j^{\prime }$, we have that
On the other hand, from (4.20) we have ![]() $t_{\gamma } = e^{{\Sigma \epsilon _i\delta _i^{\prime }}/{h}}t$ and, therefore,
$t_{\gamma } = e^{{\Sigma \epsilon _i\delta _i^{\prime }}/{h}}t$ and, therefore,
Thus, ![]() $\nabla$ is
$\nabla$ is ![]() $\alpha$-invariant. Let us show that
$\alpha$-invariant. Let us show that ![]() $\nabla$ is also
$\nabla$ is also ![]() $\operatorname {Sp}_{2n}$-invariant. Indeed, the morphism
$\operatorname {Sp}_{2n}$-invariant. Indeed, the morphism ![]() $\{f: \operatorname {Lie}(\widetilde {\alpha }) \rightarrow \operatorname {Lie}(\hat {{\mathbb {W}}})\}$ coincides with the differential of
$\{f: \operatorname {Lie}(\widetilde {\alpha }) \rightarrow \operatorname {Lie}(\hat {{\mathbb {W}}})\}$ coincides with the differential of ![]() $t$, which is, as we observed above, a unique linear map compatible with the restricted power operation. Therefore, it is
$t$, which is, as we observed above, a unique linear map compatible with the restricted power operation. Therefore, it is ![]() $\operatorname {Sp}_{2n}$-invariant.
$\operatorname {Sp}_{2n}$-invariant.
Define ![]() $S_{\alpha }$ to be the group scheme of automorphisms of the scheme
$S_{\alpha }$ to be the group scheme of automorphisms of the scheme ![]() $\alpha$, that is,
$\alpha$, that is,
Define also ![]() $S_{\widetilde {\alpha }}^{\hat {{\mathbb {W}}}}$ to be the fpqc sheaf of automorphisms of the torsor
$S_{\widetilde {\alpha }}^{\hat {{\mathbb {W}}}}$ to be the fpqc sheaf of automorphisms of the torsor ![]() $\widetilde {\alpha }$, that is,
$\widetilde {\alpha }$, that is,
Finally, define ![]() $S_{\widetilde {\alpha }}^{\nabla }$ to be subsheaf of
$S_{\widetilde {\alpha }}^{\nabla }$ to be subsheaf of ![]() $S_{\widetilde {\alpha }}^{\hat {{\mathbb {W}}}}$ of endomorphisms preserving the connection
$S_{\widetilde {\alpha }}^{\hat {{\mathbb {W}}}}$ of endomorphisms preserving the connection ![]() $\nabla$ on
$\nabla$ on ![]() $\widetilde {\alpha }$.
$\widetilde {\alpha }$.
Lemma 4.14 The morphism ![]() $S_{\widetilde {\alpha }}^{\hat {{\mathbb {W}}}} \rightarrow S_{\alpha }$ fits into a short exact sequence
$S_{\widetilde {\alpha }}^{\hat {{\mathbb {W}}}} \rightarrow S_{\alpha }$ fits into a short exact sequence
Moreover, the kernel of the composition ![]() $S_{\widetilde {\alpha }}^{\nabla } \hookrightarrow S_{\widetilde {\alpha }}^{\hat {{\mathbb {W}}}} \to S_{\alpha }$ is the sheaf
$S_{\widetilde {\alpha }}^{\nabla } \hookrightarrow S_{\widetilde {\alpha }}^{\hat {{\mathbb {W}}}} \to S_{\alpha }$ is the sheaf ![]() $\hat {{\mathbb {W}}} \subset \operatorname {Mor}(\alpha, \hat {{\mathbb {W}}})$ of constant maps. Finally, the image of
$\hat {{\mathbb {W}}} \subset \operatorname {Mor}(\alpha, \hat {{\mathbb {W}}})$ of constant maps. Finally, the image of ![]() $S_{\widetilde {\alpha }}^{\nabla }$ in
$S_{\widetilde {\alpha }}^{\nabla }$ in ![]() $S_{\alpha }$ belongs to
$S_{\alpha }$ belongs to ![]() $G_0$.
$G_0$.
Proof. The map ![]() $\operatorname {Mor}(\alpha, \hat {{\mathbb {W}}}) \rightarrow S_{\widetilde {\alpha }}$ takes
$\operatorname {Mor}(\alpha, \hat {{\mathbb {W}}}) \rightarrow S_{\widetilde {\alpha }}$ takes ![]() $f$ to the translation by
$f$ to the translation by ![]() $f \circ \pi$, and exactness is immediate because
$f \circ \pi$, and exactness is immediate because ![]() $\widetilde {\alpha }$ is a trivial torsor. If the translation by
$\widetilde {\alpha }$ is a trivial torsor. If the translation by ![]() $f \circ \pi$ preserves the connection, then
$f \circ \pi$ preserves the connection, then ![]() $df = 0$. This implies that
$df = 0$. This implies that ![]() $f$ is constant, that is,
$f$ is constant, that is, ![]() $f \in \hat {{\mathbb {W}}}$.
$f \in \hat {{\mathbb {W}}}$.
To see that ![]() $\operatorname {Im}(S_{\widetilde {\alpha }}^{\nabla }) \subset G_0$ pick
$\operatorname {Im}(S_{\widetilde {\alpha }}^{\nabla }) \subset G_0$ pick ![]() $\gamma \in S_{\widetilde {\alpha }}^{\nabla }$ and let
$\gamma \in S_{\widetilde {\alpha }}^{\nabla }$ and let ![]() $\bar \gamma$ be its image in
$\bar \gamma$ be its image in ![]() $S_{\alpha }$. We have that
$S_{\alpha }$. We have that
for some ![]() $c= (1 + \Sigma _{i>0} a_i h^{-i})\in \hat {{\mathbb {W}}}(\alpha )$. Consider the group homomorphism
$c= (1 + \Sigma _{i>0} a_i h^{-i})\in \hat {{\mathbb {W}}}(\alpha )$. Consider the group homomorphism ![]() $\hat {{\mathbb {W}}} \rightarrow \mathbb {G}_a$ that takes a series
$\hat {{\mathbb {W}}} \rightarrow \mathbb {G}_a$ that takes a series ![]() $(1 + \Sigma a_i h^{-i}) \in \hat {{\mathbb {W}}}(\alpha )$ to
$(1 + \Sigma a_i h^{-i}) \in \hat {{\mathbb {W}}}(\alpha )$ to ![]() $a_1$. This defines a morphism
$a_1$. This defines a morphism ![]() $\Omega _{\alpha }^1 \otimes \operatorname {Lie}(\hat {{\mathbb {W}}}) \rightarrow \Omega _{\alpha }^1$, and the image of
$\Omega _{\alpha }^1 \otimes \operatorname {Lie}(\hat {{\mathbb {W}}}) \rightarrow \Omega _{\alpha }^1$, and the image of ![]() $\nabla (t) \in \Omega _{\alpha }^1 \otimes \operatorname {Lie}(\hat {{\mathbb {W}}})$ is precisely
$\nabla (t) \in \Omega _{\alpha }^1 \otimes \operatorname {Lie}(\hat {{\mathbb {W}}})$ is precisely ![]() $\eta$. Hence, we have from (4.21)
$\eta$. Hence, we have from (4.21)
as desired.
Recall from Lemma 4.7 that the extension ![]() $\widetilde G^e_0 \to G_0$ admits a unique splitting
$\widetilde G^e_0 \to G_0$ admits a unique splitting ![]() $G^0_0 \hookrightarrow \widetilde G^e_0$ over
$G^0_0 \hookrightarrow \widetilde G^e_0$ over ![]() $G^0_0$. The left action of
$G^0_0$. The left action of ![]() $\widetilde G^e_0$ on
$\widetilde G^e_0$ on ![]() $\widetilde G^e_0/G^0_0 \buildrel {\sim }\over {\longrightarrow } \widetilde {\alpha }$ defines a homomorphism
$\widetilde G^e_0/G^0_0 \buildrel {\sim }\over {\longrightarrow } \widetilde {\alpha }$ defines a homomorphism
Theorem 3 Let ![]() $\nabla$ be a
$\nabla$ be a ![]() $\operatorname {Sp}_{2n} \ltimes \alpha$-invariant connection on
$\operatorname {Sp}_{2n} \ltimes \alpha$-invariant connection on ![]() $\tilde {\alpha }$. Then homomorphism (4.22) induces an isomorphism
$\tilde {\alpha }$. Then homomorphism (4.22) induces an isomorphism ![]() $\widetilde G^e_0 \buildrel {\sim }\over {\longrightarrow } S_{\widetilde {\alpha }} ^\nabla$.
$\widetilde G^e_0 \buildrel {\sim }\over {\longrightarrow } S_{\widetilde {\alpha }} ^\nabla$.
Proof. Let us show that ![]() $\widetilde G^e_0$ is a subsheaf of
$\widetilde G^e_0$ is a subsheaf of ![]() $S_{\widetilde {\alpha }}^{\nabla }$, that is,
$S_{\widetilde {\alpha }}^{\nabla }$, that is, ![]() $\nabla$ is
$\nabla$ is ![]() $G_0$-invariant. Denote by
$G_0$-invariant. Denote by ![]() $H$ the commutator subgroup of
$H$ the commutator subgroup of ![]() $G_0$. We shall first show that
$G_0$. We shall first show that ![]() $\nabla$ is
$\nabla$ is ![]() $H$-invariant.
$H$-invariant.
By Lemma 4.6 the group ![]() $H$ is generated by
$H$ is generated by ![]() $\alpha$,
$\alpha$, ![]() $\operatorname {Sp}(2n)$, and a certain one-parameter subgroup
$\operatorname {Sp}(2n)$, and a certain one-parameter subgroup ![]() $\lambda (\tau ): {\mathbb {G}}_a \to G^0_0$. By assumption,
$\lambda (\tau ): {\mathbb {G}}_a \to G^0_0$. By assumption, ![]() $\nabla$ is
$\nabla$ is ![]() $\operatorname {Sp}_{2n} \ltimes \alpha$-invariant. It remains to check that
$\operatorname {Sp}_{2n} \ltimes \alpha$-invariant. It remains to check that ![]() $\nabla$ is
$\nabla$ is ![]() ${\mathbb {G}}_a$-invariant. We use formula (4.19) describing
${\mathbb {G}}_a$-invariant. We use formula (4.19) describing ![]() $\nabla$ in coordinates corresponding to the trivialization
$\nabla$ in coordinates corresponding to the trivialization ![]() $t$ of the torsor
$t$ of the torsor ![]() $\tilde {\alpha }$. First, assume that
$\tilde {\alpha }$. First, assume that ![]() $p>3$. Homomorphism
$p>3$. Homomorphism ![]() $\lambda$ has a unique lifting
$\lambda$ has a unique lifting ![]() $\tilde {\lambda }$ to
$\tilde {\lambda }$ to ![]() $\widetilde G^{0,e}_0$ that can be explicitly computed using the construction from Lemma 4.5
$\widetilde G^{0,e}_0$ that can be explicitly computed using the construction from Lemma 4.5
The invariance of ![]() $\nabla$ under the action of
$\nabla$ under the action of ![]() ${\mathbb {G}}_a$ reads as
${\mathbb {G}}_a$ reads as
where ![]() $t': {\mathbb {G}}_a \times \alpha \to \widetilde {\alpha }$ is the composition
$t': {\mathbb {G}}_a \times \alpha \to \widetilde {\alpha }$ is the composition
We have to compute ![]() $t'$. The following equality of morphisms
$t'$. The following equality of morphisms ![]() ${\mathbb {G}}_a \times \alpha \to \widetilde G^e_0$ holds:
${\mathbb {G}}_a \times \alpha \to \widetilde G^e_0$ holds:
We claim that the last factor ![]() $e^{ {\tau ((x_1+ \delta _1)^3 -3\delta _1^2x_1 - \delta _1^3)}/{h}}$ maps
$e^{ {\tau ((x_1+ \delta _1)^3 -3\delta _1^2x_1 - \delta _1^3)}/{h}}$ maps ![]() ${\mathbb {G}}_a \times \alpha$ to
${\mathbb {G}}_a \times \alpha$ to ![]() $G_0^0\subset \widetilde G^e_0$ as follows.
$G_0^0\subset \widetilde G^e_0$ as follows.

Indeed, the same formula defines an extension of the morphism ![]() ${\mathbb {G}}_a \times \alpha \to \widetilde G^e_0$ to a morphism from a reduced scheme
${\mathbb {G}}_a \times \alpha \to \widetilde G^e_0$ to a morphism from a reduced scheme ![]() ${\mathbb {G}}_a \times \operatorname {Spec} k[[\epsilon _i, \delta _j]]$ to
${\mathbb {G}}_a \times \operatorname {Spec} k[[\epsilon _i, \delta _j]]$ to ![]() $\widetilde G^e_0$.Footnote 12 The composition of the latter with the projection
$\widetilde G^e_0$.Footnote 12 The composition of the latter with the projection ![]() $\widetilde G^e_0 \to G_0$ lands in
$\widetilde G^e_0 \to G_0$ lands in ![]() $G^0_0 \subset G_0$. But the projection
$G^0_0 \subset G_0$. But the projection ![]() $\widetilde {G}^{0,e}_0 \to G^0_0$ induces an isomorphism on points with values in any reduced
$\widetilde {G}^{0,e}_0 \to G^0_0$ induces an isomorphism on points with values in any reduced ![]() $k$-algebra. Thus, the morphism
$k$-algebra. Thus, the morphism ![]() $e^{{\tau ((x_1 + \delta _1)^3 -3\delta _1^2x_1 - \delta _1^3)}/{h}}: {\mathbb {G}}_a \times \operatorname {Spec} k[[\epsilon _i, \delta _j]] \to \widetilde G^e_0$ factors through
$e^{{\tau ((x_1 + \delta _1)^3 -3\delta _1^2x_1 - \delta _1^3)}/{h}}: {\mathbb {G}}_a \times \operatorname {Spec} k[[\epsilon _i, \delta _j]] \to \widetilde G^e_0$ factors through ![]() $G_0^0$ and the claim follows.
$G_0^0$ and the claim follows.
For ![]() $p = 3$, the lift
$p = 3$, the lift ![]() $\tilde {\gamma }$ is given by
$\tilde {\gamma }$ is given by ![]() $e^{\tau ({x_1^2y_1}/{h})}$. Write
$e^{\tau ({x_1^2y_1}/{h})}$. Write
for some uniquely determined ![]() $s \in G_0^0({\mathbb {G}}_a \times \alpha ) \subset \widetilde {G}^{0,e}_0({\mathbb {G}}_a \times \alpha )$ and
$s \in G_0^0({\mathbb {G}}_a \times \alpha ) \subset \widetilde {G}^{0,e}_0({\mathbb {G}}_a \times \alpha )$ and ![]() $f(\tau, \epsilon _1, \delta _1) \in \hat {{\mathbb {W}}}({\mathbb {G}}_a \times \alpha )$. We claim that
$f(\tau, \epsilon _1, \delta _1) \in \hat {{\mathbb {W}}}({\mathbb {G}}_a \times \alpha )$. We claim that
A direct verification of this formula is unpleasant; instead we deduce it from the following facts. Using a computation in Lie algebras from Lemma 4.8 one verifies (4.26) modulo ![]() $\tau ^2$.
$\tau ^2$.
Also, it is easy to see that the left-hand side is invariant under the action of the multiplicative group given by ![]() $\tau \to {\tau }/{a}$,
$\tau \to {\tau }/{a}$, ![]() $\epsilon _1 \to {\epsilon _1}/{a}$,
$\epsilon _1 \to {\epsilon _1}/{a}$, ![]() $\delta _1\to a\delta _1$,
$\delta _1\to a\delta _1$, ![]() $x_1 \to ax_1$,
$x_1 \to ax_1$, ![]() $y_1 \to {y}/{a}$. Thus, the element
$y_1 \to {y}/{a}$. Thus, the element ![]() $f(\tau, \epsilon _1, \delta _1)$ must be also invariant under this transformation. Finally,
$f(\tau, \epsilon _1, \delta _1)$ must be also invariant under this transformation. Finally, ![]() $f(\tau, \epsilon _1, \delta _1)$ satisfies the following cocycle condition:
$f(\tau, \epsilon _1, \delta _1)$ satisfies the following cocycle condition:
There exists a unique ![]() $f$ satisfying the above properties and it is given by (4.26). It follows that
$f$ satisfying the above properties and it is given by (4.26). It follows that ![]() $\tilde {\gamma }$ carries the section
$\tilde {\gamma }$ carries the section ![]() $t$ to
$t$ to ![]() $t'= e^{\tau ({2\delta _i^2\epsilon _i}/{h})} t$ and (4.23) follows.
$t'= e^{\tau ({2\delta _i^2\epsilon _i}/{h})} t$ and (4.23) follows.
We have proved that ![]() $\nabla$ is
$\nabla$ is ![]() $H$-invariant. Note that since
$H$-invariant. Note that since ![]() $\operatorname {Sp}_{2n} \subset H$ and
$\operatorname {Sp}_{2n} \subset H$ and ![]() $\alpha \subset H$ we can see that
$\alpha \subset H$ we can see that ![]() $\nabla$ is a unique
$\nabla$ is a unique ![]() $H$-invariant connection.
$H$-invariant connection.
The group scheme ![]() $G_0$ acts on
$G_0$ acts on ![]() $\underline {\operatorname {Conn}}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$, the subgroup
$\underline {\operatorname {Conn}}(\widetilde {\alpha }, \hat {{\mathbb {W}}})$, the subgroup ![]() $H$ is normal in
$H$ is normal in ![]() $G_0$, hence
$G_0$, hence ![]() $G_0/H$ acts on the space of
$G_0/H$ acts on the space of ![]() $H$-invariant connections. But since the latter consists of one element this action must by trivial. Hence,
$H$-invariant connections. But since the latter consists of one element this action must by trivial. Hence, ![]() $\nabla$ is
$\nabla$ is ![]() $G_0$-invariant.
$G_0$-invariant.
It follows that homomorphism (4.22) factors through ![]() $S_{\widetilde {\alpha }} ^\nabla$. Thus, by Lemma 4.14 we have a commutative diagram
$S_{\widetilde {\alpha }} ^\nabla$. Thus, by Lemma 4.14 we have a commutative diagram

where ![]() $\beta$ induces an isomorphism on the kernels of the vertical arrows. Hence,
$\beta$ induces an isomorphism on the kernels of the vertical arrows. Hence, ![]() $\beta$ is an isomorphism as desired.
$\beta$ is an isomorphism as desired.
4.4 Proof of the Basic Lemma
We will prove the assertion for the extensions by ![]() $\hat {{\mathbb {W}}}$ (as opposed to
$\hat {{\mathbb {W}}}$ (as opposed to ![]() $\operatorname {Gr}_{{\mathbb {G}}_m}$) which is a priori stronger than that stated in § 1.8.
$\operatorname {Gr}_{{\mathbb {G}}_m}$) which is a priori stronger than that stated in § 1.8.
Recall the setup. Let ![]() $i: V\hookrightarrow V^{\flat }$ be a morphism of symplectic vector spaces such that the restriction to
$i: V\hookrightarrow V^{\flat }$ be a morphism of symplectic vector spaces such that the restriction to ![]() $V$ of the symplectic form on
$V$ of the symplectic form on ![]() $V^{\flat }$ is
$V^{\flat }$ is ![]() $\omega _V$. Let
$\omega _V$. Let ![]() $\widetilde G^e_0 \to G_0$ and
$\widetilde G^e_0 \to G_0$ and ![]() $\widetilde G^{\flat, e}_0 \to G_0^{\flat }$ be the corresponding extensions. Denote by
$\widetilde G^{\flat, e}_0 \to G_0^{\flat }$ be the corresponding extensions. Denote by ![]() $G_0^{\sharp }\subset G_0^\flat$ the group subscheme that consists of automorphisms preserving kernel of the homomorphism
$G_0^{\sharp }\subset G_0^\flat$ the group subscheme that consists of automorphisms preserving kernel of the homomorphism ![]() $i^*: A_0^{\flat } \to A_0$. We have a natural homomorphism
$i^*: A_0^{\flat } \to A_0$. We have a natural homomorphism ![]() $G_0^{\sharp } \to G_0$.
$G_0^{\sharp } \to G_0$.
Theorem 4 (Basic Lemma)
The homomorphism ![]() $G_0^{\sharp } \to G_0$ lifts uniquely to a homomorphism of central extensions
$G_0^{\sharp } \to G_0$ lifts uniquely to a homomorphism of central extensions
Proof. The uniqueness follows from Corollary A.3. Let us prove the existence. By Corollary 4.12 the morphism ![]() $i: \alpha \rightarrow \alpha ^{\flat }$ lifts uniquely to a morphism
$i: \alpha \rightarrow \alpha ^{\flat }$ lifts uniquely to a morphism ![]() $\tilde {i}: \widetilde {\alpha } \rightarrow \widetilde {\alpha }^{\flat }$ of extensions. Moreover, the pullback of the (unique)
$\tilde {i}: \widetilde {\alpha } \rightarrow \widetilde {\alpha }^{\flat }$ of extensions. Moreover, the pullback of the (unique) ![]() $\operatorname {Sp} (V^\flat ) \ltimes \alpha ^\flat$-invariant connection
$\operatorname {Sp} (V^\flat ) \ltimes \alpha ^\flat$-invariant connection ![]() $\nabla ^\flat$ on
$\nabla ^\flat$ on ![]() $\widetilde {\alpha }^{\flat }$ is the (unique)
$\widetilde {\alpha }^{\flat }$ is the (unique) ![]() $\operatorname {Sp} (V) \ltimes \alpha$-invariant connection
$\operatorname {Sp} (V) \ltimes \alpha$-invariant connection ![]() $\nabla$ on
$\nabla$ on ![]() $\widetilde {\alpha }$. Thus, we have a homomorphism
$\widetilde {\alpha }$. Thus, we have a homomorphism
lifting ![]() $G_0^{\sharp } \to G_0$. It remains to apply Theorem 3.
$G_0^{\sharp } \to G_0$. It remains to apply Theorem 3.
Corollary 4.15 There exists a unique isomorphism of central extensions of ![]() $G_0^{\sharp }$:
$G_0^{\sharp }$:
4.5 Proof of the Proposition 3.3
We will prove a stronger assertion for the extensions by ![]() $\hat {{\mathbb {W}}}$ (as opposed to
$\hat {{\mathbb {W}}}$ (as opposed to ![]() $\operatorname {Gr}_{{\mathbb {G}}_m}$). Let
$\operatorname {Gr}_{{\mathbb {G}}_m}$). Let ![]() $(V, \omega )$ be a symplectic vector space and let
$(V, \omega )$ be a symplectic vector space and let ![]() $\eta$ be a homogeneous
$\eta$ be a homogeneous ![]() $1$-form on the scheme
$1$-form on the scheme ![]() ${\bf V}$ whose differential equals
${\bf V}$ whose differential equals ![]() $\omega$, that is, a vector
$\omega$, that is, a vector ![]() $\eta \in V^*\otimes V^*$ whose skew-symmetrization is
$\eta \in V^*\otimes V^*$ whose skew-symmetrization is ![]() $\omega$. Denote by
$\omega$. Denote by
the linear morphism corresponding to the graph ![]() $\Gamma _\eta : {\bf V} \hookrightarrow {\mathbb {T}}^*_ {\bf V}$ of
$\Gamma _\eta : {\bf V} \hookrightarrow {\mathbb {T}}^*_ {\bf V}$ of ![]() $\eta$. Explicitly, the composition of
$\eta$. Explicitly, the composition of ![]() $i$ with the first projection is
$i$ with the first projection is ![]() $\operatorname {Id}$ and its composition
$\operatorname {Id}$ and its composition ![]() $V\to V^*$ with the second projection is given by
$V\to V^*$ with the second projection is given by ![]() $\eta \in V^*\otimes V^*$. In § 3.2 we defined a homomorphism
$\eta \in V^*\otimes V^*$. In § 3.2 we defined a homomorphism ![]() $\psi _0: G_0 \to G_0^\flat$. We have to prove that
$\psi _0: G_0 \to G_0^\flat$. We have to prove that ![]() $\psi _0$ lifts uniquely to a homomorphism
$\psi _0$ lifts uniquely to a homomorphism ![]() $\tilde {\psi }_0: \widetilde G^e_0 \to \widetilde G^{\flat, e}_0$ of extensions. The uniqueness follows from Corollary A.3. To prove the existence we observe that by construction of
$\tilde {\psi }_0: \widetilde G^e_0 \to \widetilde G^{\flat, e}_0$ of extensions. The uniqueness follows from Corollary A.3. To prove the existence we observe that by construction of ![]() $\psi _0$ it factors through the subgroup
$\psi _0$ it factors through the subgroup ![]() $G_0^{\sharp } \subset G_0^\flat$ that consists of automorphisms preserving kernel of the homomorphism
$G_0^{\sharp } \subset G_0^\flat$ that consists of automorphisms preserving kernel of the homomorphism ![]() $i^*: A_0^{\flat } \to A_0$ and its composition
$i^*: A_0^{\flat } \to A_0$ and its composition
with restriction morphism is the identity.Footnote 13 Consider the homomorphism
Using Corollary 4.15 we get a morphism
Its composition with ![]() $(\operatorname {Id}, \psi _0)$ is the desired lift
$(\operatorname {Id}, \psi _0)$ is the desired lift ![]() $\tilde {\psi }_0: \widetilde G^e_0 \to \widetilde G^{\flat, e}_0$.
$\tilde {\psi }_0: \widetilde G^e_0 \to \widetilde G^{\flat, e}_0$.
5.  ${\mathbb {G}}_m$-equivariant quantizations
${\mathbb {G}}_m$-equivariant quantizations
In this section we consider quantizations of symplectic varieties ![]() $(X, \omega )$ equipped with an action of the multiplicative group
$(X, \omega )$ equipped with an action of the multiplicative group ![]() ${\mathbb {G}}_m$ such that the form
${\mathbb {G}}_m$ such that the form ![]() $\omega$ has a positive weight
$\omega$ has a positive weight ![]() $m$ with respect to this action and
$m$ with respect to this action and ![]() $m$ is invertible in
$m$ is invertible in ![]() $k$. We recall the notion of a
$k$. We recall the notion of a ![]() ${\mathbb {G}}_m$-equivariant Frobenius constant quantization
${\mathbb {G}}_m$-equivariant Frobenius constant quantization ![]() $O_h$ of such
$O_h$ of such ![]() $(X, \omega )$. By definition,
$(X, \omega )$. By definition, ![]() $O_h$ is a
$O_h$ is a ![]() ${\mathbb {G}}_m$-equivariant sheaf of
${\mathbb {G}}_m$-equivariant sheaf of ![]() ${\mathcal {O}}_{X'[h]}$-algebras on
${\mathcal {O}}_{X'[h]}$-algebras on ![]() $X' \times \operatorname {Spec} k[h]$. In particular, specializing
$X' \times \operatorname {Spec} k[h]$. In particular, specializing ![]() $h=1$ we have a sheaf
$h=1$ we have a sheaf ![]() $O_{h=1}$ of
$O_{h=1}$ of ![]() ${\mathcal {O}}_{X'}$-algebras over
${\mathcal {O}}_{X'}$-algebras over ![]() $X'$. We show that if the action of
$X'$. We show that if the action of ![]() ${\mathbb {G}}_m$ on
${\mathbb {G}}_m$ on ![]() $X$ is contracting, then
$X$ is contracting, then ![]() $O_{h=1}$ is an Azumaya algebra over
$O_{h=1}$ is an Azumaya algebra over ![]() $X'$ and using Theorem 1 compute its class in the Brauer group
$X'$ and using Theorem 1 compute its class in the Brauer group ![]() $\operatorname {Br}(X')$ proving a conjecture of Kubrak and Travkin [Reference Kubrak and TravkinKT19].
$\operatorname {Br}(X')$ proving a conjecture of Kubrak and Travkin [Reference Kubrak and TravkinKT19].
5.1 Definition of  ${\mathbb {G}}_m$-equivariant quantizations
${\mathbb {G}}_m$-equivariant quantizations
Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $k$ equipped with a symplectic
$k$ equipped with a symplectic ![]() $2$-form
$2$-form ![]() $\omega$ and a
$\omega$ and a ![]() ${\mathbb {G}}_m$-action
${\mathbb {G}}_m$-action
We shall say that ![]() $\omega$ is of weight
$\omega$ is of weight ![]() $m$ with respect to the
$m$ with respect to the ![]() ${\mathbb {G}}_m$-action if the following identity holds in
${\mathbb {G}}_m$-action if the following identity holds in ![]() $\Gamma ({\mathbb {G}}_m \times X, \Omega ^2_{ {\mathbb {G}}_m \times X/{\mathbb {G}}_m})$:
$\Gamma ({\mathbb {G}}_m \times X, \Omega ^2_{ {\mathbb {G}}_m \times X/{\mathbb {G}}_m})$:
Here ![]() $z$ denotes the coordinate on
$z$ denotes the coordinate on ![]() ${\mathbb {G}}_m$ and
${\mathbb {G}}_m$ and ![]() $\operatorname {pr}_X: {\mathbb {G}}_m \times X \to X$ the projection. For the duration of this section we shall assume that
$\operatorname {pr}_X: {\mathbb {G}}_m \times X \to X$ the projection. For the duration of this section we shall assume that ![]() $\omega$ is of weight
$\omega$ is of weight ![]() $m$ with
$m$ with ![]() $m$ invertible in
$m$ invertible in ![]() $k$.
$k$.
The ![]() ${\mathbb {G}}_m$-action on
${\mathbb {G}}_m$-action on ![]() $X$ defines a homomorphism from the Lie algebra of
$X$ defines a homomorphism from the Lie algebra of ![]() ${\mathbb {G}}_m$ to the Lie algebra of vector fields on
${\mathbb {G}}_m$ to the Lie algebra of vector fields on ![]() $X$. Denote by
$X$. Denote by ![]() $\theta$ the image of the generator of
$\theta$ the image of the generator of ![]() $\operatorname {Lie} {\mathbb {G}}_m$. Formula (5.2) together with the identity
$\operatorname {Lie} {\mathbb {G}}_m$. Formula (5.2) together with the identity ![]() $d\omega =0$ imply that
$d\omega =0$ imply that
Hence, setting ![]() $\eta = ({1}/{m}) \iota _{\theta } \omega$, defines a restricted Poisson structure on
$\eta = ({1}/{m}) \iota _{\theta } \omega$, defines a restricted Poisson structure on ![]() $X$. Endow
$X$. Endow ![]() $X'[h]\colon = X' \times \operatorname {Spec} k[h]$ with the
$X'[h]\colon = X' \times \operatorname {Spec} k[h]$ with the ![]() ${\mathbb {G}}_m$-action given by the composition
${\mathbb {G}}_m$-action given by the composition
(where ![]() $F: {\mathbb {G}}_m \to {\mathbb {G}}_m$ is given by
$F: {\mathbb {G}}_m \to {\mathbb {G}}_m$ is given by ![]() $F^*(z) =z^p$) on the first factor and by
$F^*(z) =z^p$) on the first factor and by ![]() $h\mapsto z^m h$ on the second factor.
$h\mapsto z^m h$ on the second factor.
A ![]() ${\mathbb {G}}_m$-equivariant Frobenius-constant quantization of
${\mathbb {G}}_m$-equivariant Frobenius-constant quantization of ![]() $X$ consists of a
$X$ consists of a ![]() ${\mathbb {G}}_m$-equivariant sheaf
${\mathbb {G}}_m$-equivariant sheaf ![]() $O_h$ of associative
$O_h$ of associative ![]() ${\mathcal {O}}_{X'[h]}$-algebras on
${\mathcal {O}}_{X'[h]}$-algebras on ![]() $X'[h]$ together with an isomorphism of
$X'[h]$ together with an isomorphism of ![]() ${\mathbb {G}}_m$-equivariant
${\mathbb {G}}_m$-equivariant ![]() ${\mathcal {O}}_{X'}$-algebras
${\mathcal {O}}_{X'}$-algebras
such that ![]() $O_h$ is locally free as an
$O_h$ is locally free as an ![]() ${\mathcal {O}}_{X'[h]}$-module and the restriction
${\mathcal {O}}_{X'[h]}$-module and the restriction ![]() ${\mathcal {O}}_h:= \lim O_h/(h^n)$ of
${\mathcal {O}}_h:= \lim O_h/(h^n)$ of ![]() $O_h$ to the formal completion of
$O_h$ to the formal completion of ![]() $X'[h]$ along the divisor
$X'[h]$ along the divisor ![]() $h=0$ (equipped with the central homomorphism
$h=0$ (equipped with the central homomorphism ![]() $s: {\mathcal {O}}_{X'}[[h]] \to {\mathcal {O}}_h$ and (5.3)) is a Frobenius-constant quantization of
$s: {\mathcal {O}}_{X'}[[h]] \to {\mathcal {O}}_h$ and (5.3)) is a Frobenius-constant quantization of ![]() $X$ compatible with the restricted Poisson structure given by the
$X$ compatible with the restricted Poisson structure given by the ![]() $1$-form
$1$-form ![]() $\eta = ({1}/{m}) \iota _{\theta } \omega$.
$\eta = ({1}/{m}) \iota _{\theta } \omega$.
For example, if ![]() $X$ is affine, then a
$X$ is affine, then a ![]() ${\mathbb {G}}_m$-equivariant Frobenius-constant quantization of
${\mathbb {G}}_m$-equivariant Frobenius-constant quantization of ![]() $X$ is determined by a graded
$X$ is determined by a graded ![]() ${\mathcal {O}}(X')[h]$-algebra
${\mathcal {O}}(X')[h]$-algebra ![]() $O_h(X'[h])$ (with
$O_h(X'[h])$ (with ![]() $\deg h=m$) together with
$\deg h=m$) together with ![]() $O_h(X'[h])/(h)\buildrel {\sim }\over {\longrightarrow } {\mathcal {O}}(X)$.
$O_h(X'[h])/(h)\buildrel {\sim }\over {\longrightarrow } {\mathcal {O}}(X)$.
5.2  ${\mathbb {A}}^1$-action
${\mathbb {A}}^1$-action
In the following, we shall consider ![]() ${\mathbb {G}}_m$-actions on a scheme
${\mathbb {G}}_m$-actions on a scheme ![]() $X$ satisfying the property that: morphism (5.2) extends to a morphism
$X$ satisfying the property that: morphism (5.2) extends to a morphism
If ![]() $X$ is reduced and separated, which we shall assume to be the case for rest of this section, then
$X$ is reduced and separated, which we shall assume to be the case for rest of this section, then ![]() $\tilde {\lambda }$ defines an action of the monoid
$\tilde {\lambda }$ defines an action of the monoid ![]() ${\mathbb {A}}^1$ on
${\mathbb {A}}^1$ on ![]() $X$. In particular, the restriction of
$X$. In particular, the restriction of ![]() $\tilde {\lambda }$ to the closed subscheme
$\tilde {\lambda }$ to the closed subscheme ![]() $X \hookrightarrow {\mathbb {A}}^1 \times X$ given by the equation
$X \hookrightarrow {\mathbb {A}}^1 \times X$ given by the equation ![]() $z=0$ factors through the subscheme
$z=0$ factors through the subscheme ![]() $X^{{\mathbb {G}}_m} \hookrightarrow X$ of fixed points:
$X^{{\mathbb {G}}_m} \hookrightarrow X$ of fixed points:
Moreover, ![]() $\tilde {\lambda }$ exhibits
$\tilde {\lambda }$ exhibits ![]() $X^{{\mathbb {G}}_m}$ as a
$X^{{\mathbb {G}}_m}$ as a ![]() ${\mathbb {A}}^1$-homotopy retract of
${\mathbb {A}}^1$-homotopy retract of ![]() $X$.
$X$.
Also note if ![]() $X$ is a proper scheme with a nontrivial action of
$X$ is a proper scheme with a nontrivial action of ![]() ${\mathbb {G}}_m$, then
${\mathbb {G}}_m$, then ![]() $\tilde {\lambda }$ does not exist. This can be seen by looking at the closure of a
$\tilde {\lambda }$ does not exist. This can be seen by looking at the closure of a ![]() $1$-dimensional
$1$-dimensional ![]() ${\mathbb {G}}_m$-orbit in
${\mathbb {G}}_m$-orbit in ![]() $X$.
$X$.
5.3 Main result
By definition, a ![]() ${\mathbb {G}}_m$-equivariant Frobenius-constant quantization
${\mathbb {G}}_m$-equivariant Frobenius-constant quantization ![]() $O_h$ gives rise to a Frobenius-constant quantization
$O_h$ gives rise to a Frobenius-constant quantization ![]() ${\mathcal {O}}_h$ and, thus, a class
${\mathcal {O}}_h$ and, thus, a class ![]() $\rho (O_h)\in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$ (see § 1.4). Denote by
$\rho (O_h)\in H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )$ (see § 1.4). Denote by ![]() $[\rho (O_h)] \in \operatorname {Br} (X')$ the image of
$[\rho (O_h)] \in \operatorname {Br} (X')$ the image of ![]() $\rho (O_h)$ under the homomorphism
$\rho (O_h)$ under the homomorphism ![]() $H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )\to H^2_{\rm et}(X', {\mathcal {O}}_{X'}^*)$.
$H^1_{\rm et}(X', {\mathcal {O}}_{X'}^*/{\mathcal {O}}_{X'}^{* p} )\to H^2_{\rm et}(X', {\mathcal {O}}_{X'}^*)$.
Recall from [Reference Ogus and VologodskyOV07, § 4.2] a homomorphism
that carries a ![]() $1$-form
$1$-form ![]() $\eta$ to the class of the Azumaya algebra
$\eta$ to the class of the Azumaya algebra ![]() $D_X$ restricted to the graph of the embedding
$D_X$ restricted to the graph of the embedding ![]() $\Gamma _\eta : X' \to {\mathbb {T}}^*_{X'}$ given by
$\Gamma _\eta : X' \to {\mathbb {T}}^*_{X'}$ given by ![]() $\eta$. Finally, denote by
$\eta$. Finally, denote by ![]() $O_{h=1}$ the sheaf of
$O_{h=1}$ the sheaf of ![]() ${\mathcal {O}}_{X'}$-algebras
${\mathcal {O}}_{X'}$-algebras ![]() $O_h/(h-1)$. The following result has been conjectured in [Reference Kubrak and TravkinKT19, § 0.3, Question 2].
$O_h/(h-1)$. The following result has been conjectured in [Reference Kubrak and TravkinKT19, § 0.3, Question 2].
Theorem 5 Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $k$ equipped with a
$k$ equipped with a ![]() ${\mathbb {G}}_m$-action (5.2) and a symplectic form
${\mathbb {G}}_m$-action (5.2) and a symplectic form ![]() $\omega$ of weight
$\omega$ of weight ![]() $m>0$ relatively prime to the characteristic of
$m>0$ relatively prime to the characteristic of ![]() $k$. Assume that the morphism (5.1) extends to a morphism (5.4). Then, for every
$k$. Assume that the morphism (5.1) extends to a morphism (5.4). Then, for every ![]() ${\mathbb {G}}_m$-equivariant Frobenius-constant quantization
${\mathbb {G}}_m$-equivariant Frobenius-constant quantization ![]() $O_h$ of
$O_h$ of ![]() $X$, the restriction of
$X$, the restriction of ![]() $O_h$ to
$O_h$ to ![]() $X'[h, h^{-1}] = X' \times \operatorname {Spec} k[h, h^{-1}] \subset X'[h]$ is an Azumaya algebra. Moreover, the following equality in
$X'[h, h^{-1}] = X' \times \operatorname {Spec} k[h, h^{-1}] \subset X'[h]$ is an Azumaya algebra. Moreover, the following equality in ![]() $\operatorname {Br}(X')$ holds:
$\operatorname {Br}(X')$ holds:
Proof. To prove the Azumaya property of ![]() $O_h(h^{-1})$ consider the morphism
$O_h(h^{-1})$ consider the morphism
This is a morphism of vector bundles over ![]() $X'[h]$ of the same rank. We have to prove that
$X'[h]$ of the same rank. We have to prove that ![]() $\psi$ is an isomorphism away from the divisor
$\psi$ is an isomorphism away from the divisor ![]() $h=0$. Denote by
$h=0$. Denote by
the determinant of ![]() $\psi$ and by
$\psi$ and by ![]() $Z\hookrightarrow X'[h]$. Let
$Z\hookrightarrow X'[h]$. Let ![]() $(x_0, h_0) \in Z$ be a
$(x_0, h_0) \in Z$ be a ![]() $k$-point of
$k$-point of ![]() $Z$. We shall check that
$Z$. We shall check that ![]() $h_0=0$. Using (5.4) and the positivity of
$h_0=0$. Using (5.4) and the positivity of ![]() $m$ the
$m$ the ![]() ${\mathbb {G}}_m$-action on
${\mathbb {G}}_m$-action on ![]() $X'[h]$ extends to a morphism
$X'[h]$ extends to a morphism
It follows that the closure ![]() $T$ of the
$T$ of the ![]() ${\mathbb {G}}_m$-orbit of
${\mathbb {G}}_m$-orbit of ![]() $(x_0, h_0)$ intersects the divisor
$(x_0, h_0)$ intersects the divisor ![]() $h=0$ at some point
$h=0$ at some point ![]() $(x_0', 0)$. Since
$(x_0', 0)$. Since ![]() $Z$ is closed and
$Z$ is closed and ![]() ${\mathbb {G}}_m$-invariant we have that
${\mathbb {G}}_m$-invariant we have that ![]() $T\subset Z$ i.e.
$T\subset Z$ i.e. ![]() $\det \psi$ is identically
$\det \psi$ is identically ![]() $0$ on
$0$ on ![]() $T$. On the other hand, using the Azumaya property of the formal quantization
$T$. On the other hand, using the Azumaya property of the formal quantization ![]() ${\mathcal {O}}_h(h^{-1})$ we see that the restriction of
${\mathcal {O}}_h(h^{-1})$ we see that the restriction of ![]() $\psi$ to the formal punctured neighborhood of
$\psi$ to the formal punctured neighborhood of ![]() $(x_0', 0)\in T$ is an isomorphism. This contradiction proves the first assertion of the theorem.
$(x_0', 0)\in T$ is an isomorphism. This contradiction proves the first assertion of the theorem.
For the second assertion, consider algebra ![]() $D_{X, h}$ obtained from the filtered algebra of differential
$D_{X, h}$ obtained from the filtered algebra of differential ![]() $D_{Y}$ operators via the Rees construction (see § 1.2). The
$D_{Y}$ operators via the Rees construction (see § 1.2). The ![]() $p$-curvature homomorphism makes
$p$-curvature homomorphism makes ![]() $D_{X, h}$ into an algebra over
$D_{X, h}$ into an algebra over ![]() $S^\cdot T_{X'}[h]$. The graph
$S^\cdot T_{X'}[h]$. The graph ![]() $\Gamma _{\eta }: X' \rightarrow \mathbb {T}_{X'}^*$ of the differential form
$\Gamma _{\eta }: X' \rightarrow \mathbb {T}_{X'}^*$ of the differential form ![]() $\eta = ({1}/{m}) \iota _{\theta } \omega$ defines a sheaf of ideals
$\eta = ({1}/{m}) \iota _{\theta } \omega$ defines a sheaf of ideals ![]() $I_{\Gamma _{\eta }} \subset S^{\cdot }T_{X'}$. The quotient
$I_{\Gamma _{\eta }} \subset S^{\cdot }T_{X'}$. The quotient ![]() $D_{X, [\eta ], h}=D_{X, h} /I_{\Gamma _{\eta }}$ can be viewed as a
$D_{X, [\eta ], h}=D_{X, h} /I_{\Gamma _{\eta }}$ can be viewed as a ![]() ${\mathbb {G}}_m$-equivariant sheaf of
${\mathbb {G}}_m$-equivariant sheaf of ![]() ${\mathcal {O}}_{X'[h]}$-algebras over
${\mathcal {O}}_{X'[h]}$-algebras over ![]() $X'[h]$. By construction, the restriction of
$X'[h]$. By construction, the restriction of ![]() $D_{X, [\eta ], h}$ to the formal completion of
$D_{X, [\eta ], h}$ to the formal completion of ![]() $X'[h]$ along the divisor
$X'[h]$ along the divisor ![]() $h=0$ is isomorphic to the algebra
$h=0$ is isomorphic to the algebra ![]() ${\mathcal {D}}_{X, [\eta ], h}$ constructed in § 1.5. Now given a
${\mathcal {D}}_{X, [\eta ], h}$ constructed in § 1.5. Now given a ![]() ${\mathbb {G}}_m$-equivariant Frobenius-constant quantization
${\mathbb {G}}_m$-equivariant Frobenius-constant quantization ![]() $O_h$ we consider the tensor product
$O_h$ we consider the tensor product ![]() $O_h \otimes _{{\mathcal {O}}_{X'}[h]} D_{X, [\eta ], h}^{\rm op}$. Using Theorem 1 and the Beauville–Laszlo theorem [Reference Beauville and LaszloBL95] there exists a sheaf
$O_h \otimes _{{\mathcal {O}}_{X'}[h]} D_{X, [\eta ], h}^{\rm op}$. Using Theorem 1 and the Beauville–Laszlo theorem [Reference Beauville and LaszloBL95] there exists a sheaf ![]() $O^\sharp _h$ of
$O^\sharp _h$ of ![]() ${\mathcal {O}}_{X'[h]}$-algebras over
${\mathcal {O}}_{X'[h]}$-algebras over ![]() $X'[h]$ whose restriction to
$X'[h]$ whose restriction to ![]() $X'[h, h^{-1}]$ is
$X'[h, h^{-1}]$ is ![]() $(O_h \otimes _{{\mathcal {O}}_{X'}[h]} D_{X, [\eta ], h}^{\rm op})(h^{-1})$ and whose restriction to the formal completion of
$(O_h \otimes _{{\mathcal {O}}_{X'}[h]} D_{X, [\eta ], h}^{\rm op})(h^{-1})$ and whose restriction to the formal completion of ![]() $X'[h]$ along the divisor
$X'[h]$ along the divisor ![]() $h=0$ is an Azumaya algebra. It follows that
$h=0$ is an Azumaya algebra. It follows that ![]() $O^\sharp _h$ is an Azumaya algebra over
$O^\sharp _h$ is an Azumaya algebra over ![]() $X'[h]$. We claim that the following equality holds in
$X'[h]$. We claim that the following equality holds in ![]() $\operatorname {Br}({\mathbb {A}}^1 \times X'[h])$:
$\operatorname {Br}({\mathbb {A}}^1 \times X'[h])$:
Indeed, since ![]() $(O_h \otimes _{{\mathcal {O}}_{X'}[h]} D_{X, [\eta ], h}^{\rm op})(h^{-1})$ is
$(O_h \otimes _{{\mathcal {O}}_{X'}[h]} D_{X, [\eta ], h}^{\rm op})(h^{-1})$ is ![]() ${\mathbb {G}}_m$-equivariant the equality holds after the restriction to
${\mathbb {G}}_m$-equivariant the equality holds after the restriction to ![]() ${\mathbb {G}}_m \times X'[h, h^{-1}]$. Now the claim follows from the injectivity of the restriction morphism
${\mathbb {G}}_m \times X'[h, h^{-1}]$. Now the claim follows from the injectivity of the restriction morphism ![]() $\operatorname {Br}({\mathbb {A}}^1 \times X'[h]) \to \operatorname {Br}({\mathbb {G}}_m \times X'[h, h^{-1}])$. Restricting the classes in (5.7) to the divisor
$\operatorname {Br}({\mathbb {A}}^1 \times X'[h]) \to \operatorname {Br}({\mathbb {G}}_m \times X'[h, h^{-1}])$. Restricting the classes in (5.7) to the divisor ![]() $X'[h] \stackrel {z=0}{\longrightarrow } {\mathbb {A}}^1 \times X'[h]$ we find that
$X'[h] \stackrel {z=0}{\longrightarrow } {\mathbb {A}}^1 \times X'[h]$ we find that
Morphism ![]() $\tilde {\lambda }(h)^*_0: X'[h] \to X'[h]$ factors as follows:
$\tilde {\lambda }(h)^*_0: X'[h] \to X'[h]$ factors as follows:
By Theorem 1 the restriction of ![]() $[O^\sharp _h]$ to the divisor
$[O^\sharp _h]$ to the divisor ![]() $X' \stackrel {h=0}{\longrightarrow } X'[h]$ is equal to
$X' \stackrel {h=0}{\longrightarrow } X'[h]$ is equal to ![]() $[\rho (O_h)]$. Using (5.8) and restricting to the divisor
$[\rho (O_h)]$. Using (5.8) and restricting to the divisor ![]() $h=1$ we find that
$h=1$ we find that
as desired.
Acknowledgements
This paper has grown out of our attempt to correct an error in [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24]. This proposition asserts, in particular, that the algebra ![]() ${\mathcal {O}}_h(h^{-1})$ extends to an Azumaya algebra over the formal scheme
${\mathcal {O}}_h(h^{-1})$ extends to an Azumaya algebra over the formal scheme ![]() $X'[[h]]$. In fact, the result stated in [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24] is similar to our formula (1.9) with the exception that the class
$X'[[h]]$. In fact, the result stated in [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24] is similar to our formula (1.9) with the exception that the class ![]() $[{\mathcal {O}}^\sharp _h]$ at the left-hand side of (1.9) is replaced by the class of an extension of
$[{\mathcal {O}}^\sharp _h]$ at the left-hand side of (1.9) is replaced by the class of an extension of ![]() ${\mathcal {O}}_h(h^{-1})$ to
${\mathcal {O}}_h(h^{-1})$ to ![]() $X'[[h]]$. In particular, [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24] asserts that the Azumaya algebra
$X'[[h]]$. In particular, [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24] asserts that the Azumaya algebra ![]() ${\mathcal {O}}_h(h^{-1})$ corresponding to the
${\mathcal {O}}_h(h^{-1})$ corresponding to the ![]() ${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant Frobenius-constant quantization splits which is definitely not the case since the algebra
${\mathbb {Z}}/2{\mathbb {Z}}$-equivariant Frobenius-constant quantization splits which is definitely not the case since the algebra ![]() ${\mathcal {O}}_h$ has no zero divisors. In § 3, Remark 3.8, we indicate where the error in the proof of [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24] is. In particular, we will see that
${\mathcal {O}}_h$ has no zero divisors. In § 3, Remark 3.8, we indicate where the error in the proof of [Reference Bezrukavnikov and KaledinBK08, Proposition 1.24] is. In particular, we will see that ![]() ${\mathcal {O}}_h(h^{-1})$ never extends to an Azumaya algebra over
${\mathcal {O}}_h(h^{-1})$ never extends to an Azumaya algebra over ![]() $X'[[h]]$.
$X'[[h]]$.
The authors would like to express their gratitude to Dmitry Kaledin. Numerous conversations with Dmitry and his encouragement helped us to overcome many of the technical and conceptual difficulties we encountered in the course of the work. The authors also benefited greatly from conversations with Michael Finkelberg and Alexander Petrov on the affine grassmannian and rigid analytic geometry, respectively. We are grateful to Roman Travkin who explained to us that one should look at quantizations of the category ![]() $\operatorname {QCoh}(X)$ rather than quantizations of the algebra
$\operatorname {QCoh}(X)$ rather than quantizations of the algebra ![]() ${\mathcal {O}}_X$. This has led to a revision of this paper as well as the appearance of a sequel paper [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22] joint with Dmitry Kubrak and Roman Travkin. Finally, we would like to thank the referee for a meticulous review.
${\mathcal {O}}_X$. This has led to a revision of this paper as well as the appearance of a sequel paper [Reference Bogdanova, Kubrak, Travkin and VologodskyBKTV22] joint with Dmitry Kubrak and Roman Travkin. Finally, we would like to thank the referee for a meticulous review.
Both authors were partially supported by the Russian Science Foundation, grant number 21-11-00153.
Conflicts of Interest
None.
Appendix A
A.1 The affine grassmannian for  ${\mathbb {G}}_m$
${\mathbb {G}}_m$
Let ![]() $G$ be an algebraic group over a field
$G$ be an algebraic group over a field ![]() $k$. Denote by
$k$. Denote by
the corresponding loop group, that is a sheaf of groups on the category of affine schemes over ![]() $k$ equipped with the fpqc topology sending
$k$ equipped with the fpqc topology sending ![]() $k$-scheme
$k$-scheme ![]() $\operatorname {Spec} R$ to
$\operatorname {Spec} R$ to ![]() $G(R((h)))$. Also, let
$G(R((h)))$. Also, let
be the sheaf of groups sending ![]() $k$-scheme
$k$-scheme ![]() $\operatorname {Spec} R$ to
$\operatorname {Spec} R$ to ![]() $G(R[[h]])$. It is known (see e.g. [Reference ZhuZhu17, Proposition 1.3.2]) that
$G(R[[h]])$. It is known (see e.g. [Reference ZhuZhu17, Proposition 1.3.2]) that ![]() $L^+G$ is represented by a group scheme over
$L^+G$ is represented by a group scheme over ![]() $k$ and that
$k$ and that ![]() $LG$ is an ind-affine scheme. Denote by
$LG$ is an ind-affine scheme. Denote by ![]() $\operatorname {Gr} _G$ the affine grassmannian for
$\operatorname {Gr} _G$ the affine grassmannian for ![]() $G$. By definition,
$G$. By definition, ![]() $\operatorname {Gr} _G$ is the fpqc sheaf associated to the presheaf
$\operatorname {Gr} _G$ is the fpqc sheaf associated to the presheaf ![]() $R \mapsto LG(R)/L^+G(R)$.
$R \mapsto LG(R)/L^+G(R)$.
Recall the structure of the affine grassmannian for ![]() ${\mathbb {G}}_m$. The following result is well-known (see, for example, [Reference Contou-CarrereCon94]); for the reader's convenience we include its proof.
${\mathbb {G}}_m$. The following result is well-known (see, for example, [Reference Contou-CarrereCon94]); for the reader's convenience we include its proof.
Lemma A.1 For a commutative ring ![]() $R$ such that
$R$ such that ![]() $\operatorname {Spec} R$ is connected there is a decomposition
$\operatorname {Spec} R$ is connected there is a decomposition
where ![]() ${\mathbb {W}}(R)$ is the subgroup of
${\mathbb {W}}(R)$ is the subgroup of ![]() $R[[h]]^*$ formed by formal power series with constant term
$R[[h]]^*$ formed by formal power series with constant term ![]() $1$,
$1$, ![]() $\hat {{\mathbb {W}}} (R)$ is the group of polynomials of the form
$\hat {{\mathbb {W}}} (R)$ is the group of polynomials of the form ![]() $1 + \Sigma a_i h^{-i}$ with nilpotent coefficients
$1 + \Sigma a_i h^{-i}$ with nilpotent coefficients ![]() $a_i \in R$. In addition, we have that
$a_i \in R$. In addition, we have that
Proof. The claim follows from the fact that under the assumptions of the lemma
 \[ R((h))^{*}=\bigg\{\sum_{i} a_{i} h^{i} \in R((h)) ; \exists i_{0}: a_{i_{0}} \in R^{*}, a_{j} \text{ nilpotent for all } j< i_{0}\bigg\}. \]
\[ R((h))^{*}=\bigg\{\sum_{i} a_{i} h^{i} \in R((h)) ; \exists i_{0}: a_{i_{0}} \in R^{*}, a_{j} \text{ nilpotent for all } j< i_{0}\bigg\}. \]
To show this replace ![]() $R$ by
$R$ by ![]() $R/ \mathfrak {N}_{R}$, where
$R/ \mathfrak {N}_{R}$, where ![]() $\mathfrak {N}_{R}$ stands for the nilradical. We need to show that a Laurent polynomial is invertible if and only if its first nonzero coefficient is invertible in
$\mathfrak {N}_{R}$ stands for the nilradical. We need to show that a Laurent polynomial is invertible if and only if its first nonzero coefficient is invertible in ![]() $R$. Suppose that
$R$. Suppose that
for ![]() $A(h), B(h) \in R((h))$ such that
$A(h), B(h) \in R((h))$ such that
 \begin{equation} \begin{aligned} A(h) = a_{-N} h^{-N} + a_{-N+1} h^{-N+1} + \cdots,\\ B(h) = b_{-N} h^{-M} + b_{-M+1} h^{-M+1} + \cdots, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} A(h) = a_{-N} h^{-N} + a_{-N+1} h^{-N+1} + \cdots,\\ B(h) = b_{-N} h^{-M} + b_{-M+1} h^{-M+1} + \cdots, \end{aligned} \end{equation}
where ![]() $b_{-M} \neq 0$ and
$b_{-M} \neq 0$ and ![]() $a_{-N} \neq 0$. From (A.1) we have that
$a_{-N} \neq 0$. From (A.1) we have that ![]() $N+M \geq 0$. If
$N+M \geq 0$. If ![]() $N+M=0$, then
$N+M=0$, then ![]() $a_{-N} b_{-M} = 1$ and we are done. Otherwise, we have from (A.1)
$a_{-N} b_{-M} = 1$ and we are done. Otherwise, we have from (A.1)
Using (A.3) we get ![]() $a_{-N}^2b_{-M+1}=0$ and similarly
$a_{-N}^2b_{-M+1}=0$ and similarly ![]() $a_{-N}^ib_{-M+i}=0$ for every
$a_{-N}^ib_{-M+i}=0$ for every ![]() $i \leq N+M$. Multiplying both sides of (A.4) by
$i \leq N+M$. Multiplying both sides of (A.4) by ![]() $a_{-N}^{N+M}$ we infer
$a_{-N}^{N+M}$ we infer
Since ![]() $a_{-N}$ and
$a_{-N}$ and ![]() $1-a_{-N}b_{-M+(N+M)}$ are coprime,
$1-a_{-N}b_{-M+(N+M)}$ are coprime,
![]() $\operatorname {Spec} R$ is connected, and
$\operatorname {Spec} R$ is connected, and ![]() $a_{-N} \neq 0$ we conclude that
$a_{-N} \neq 0$ we conclude that ![]() $1-a_{-N}b_{-M+(N+M)} = 0$. Hence,
$1-a_{-N}b_{-M+(N+M)} = 0$. Hence, ![]() $a_{-N}$ is invertible as desired.
$a_{-N}$ is invertible as desired.
Using the lemma, we have decompositions
where ![]() ${\mathbb {W}}$ is the group scheme of big Witt vectors and
${\mathbb {W}}$ is the group scheme of big Witt vectors and ![]() $\hat {{\mathbb {W}}}$ is a group ind-scheme whose group of
$\hat {{\mathbb {W}}}$ is a group ind-scheme whose group of ![]() $R$-points is defined in the lemma.
$R$-points is defined in the lemma.
A.2 Subgroups of  $L\operatorname {GL}(n)$
$L\operatorname {GL}(n)$
Proposition A.2 Let ![]() $G$ be an affine group scheme over a field
$G$ be an affine group scheme over a field ![]() $k$, and let
$k$, and let ![]() $\phi : G \to L\operatorname {GL}(n)$ be a homomorphism. Then there exists an element
$\phi : G \to L\operatorname {GL}(n)$ be a homomorphism. Then there exists an element ![]() $g\in \operatorname {GL}(n, k((h)))$ such that
$g\in \operatorname {GL}(n, k((h)))$ such that ![]() $\phi$ factors through
$\phi$ factors through ![]() $gL^+\operatorname {GL}(n)g^{-1}$:
$gL^+\operatorname {GL}(n)g^{-1}$:
Proof. Set ![]() $V=k^n$. We have to show that there exists a
$V=k^n$. We have to show that there exists a ![]() $\phi (G)$-invariant
$\phi (G)$-invariant ![]() $k[[h]]$-lattice
$k[[h]]$-lattice
Informally, our ![]() $\Lambda$ will be constructed starting with the lattice
$\Lambda$ will be constructed starting with the lattice ![]() $\Lambda _0=V[[h]]$ as the intersection
$\Lambda _0=V[[h]]$ as the intersection ![]() $\bigcap _g g \Lambda _0$. Since we make no assumptions on
$\bigcap _g g \Lambda _0$. Since we make no assumptions on ![]() $k$ and
$k$ and ![]() $G$ one has give a meaning to the latter. We shall do it as follows.
$G$ one has give a meaning to the latter. We shall do it as follows.
The morphism ![]() $\phi$ is given by a matrix
$\phi$ is given by a matrix ![]() $A\in \operatorname {GL}(n, {\mathcal {O}}(G)((h)))$ such that
$A\in \operatorname {GL}(n, {\mathcal {O}}(G)((h)))$ such that
where ![]() $\Delta : {\mathcal {O}}(G) \to {\mathcal {O}}(G)\otimes {\mathcal {O}}(G)$ is the comultiplication on
$\Delta : {\mathcal {O}}(G) \to {\mathcal {O}}(G)\otimes {\mathcal {O}}(G)$ is the comultiplication on ![]() ${\mathcal {O}}(G)$ given by the product morphism
${\mathcal {O}}(G)$ given by the product morphism ![]() $G\times G \to G$ and such that the image of
$G\times G \to G$ and such that the image of ![]() $A$ under the evaluation at
$A$ under the evaluation at ![]() $1\in G(k)$ homomorphism
$1\in G(k)$ homomorphism ![]() $\operatorname {GL}(n, {\mathcal {O}}(G)((h))) \to \operatorname {GL}(n,k((h)))$ is the identity matrix.
$\operatorname {GL}(n, {\mathcal {O}}(G)((h))) \to \operatorname {GL}(n,k((h)))$ is the identity matrix.
Set
Then ![]() $\Lambda$ is a
$\Lambda$ is a ![]() $k[[h]]$-submodule of
$k[[h]]$-submodule of ![]() $V[[h]]$ contains
$V[[h]]$ contains ![]() $h^N V[[h]]$, for sufficiently large
$h^N V[[h]]$, for sufficiently large ![]() $N$. Hence,
$N$. Hence, ![]() $\Lambda$ is a lattice. It remains to show that
$\Lambda$ is a lattice. It remains to show that ![]() $\Lambda$ is
$\Lambda$ is ![]() $\phi (G)$-invariant, that is
$\phi (G)$-invariant, that is
The matrix ![]() $A$ defines
$A$ defines ![]() ${\mathcal {O}}(G)((h))$-linear maps
${\mathcal {O}}(G)((h))$-linear maps
 \begin{equation} \begin{aligned} V((h)) \otimes_{k[[h]]} {\mathcal{O}}(G)[[h]] \stackrel{A\otimes \operatorname{Id}}{\longrightarrow} (V((h)) \otimes_{k[[h]]} {\mathcal{O}}(G)[[h]]) \otimes_ {k[[h]]} {\mathcal{O}}(G)[[h]] \to \\ \to V((h)) \otimes_{k[[h]]} ({\mathcal{O}}(G) \otimes_k {\mathcal{O}}(G))[[h]], \end{aligned} \end{equation}
\begin{equation} \begin{aligned} V((h)) \otimes_{k[[h]]} {\mathcal{O}}(G)[[h]] \stackrel{A\otimes \operatorname{Id}}{\longrightarrow} (V((h)) \otimes_{k[[h]]} {\mathcal{O}}(G)[[h]]) \otimes_ {k[[h]]} {\mathcal{O}}(G)[[h]] \to \\ \to V((h)) \otimes_{k[[h]]} ({\mathcal{O}}(G) \otimes_k {\mathcal{O}}(G))[[h]], \end{aligned} \end{equation}where the second map in (A.6) is induced by the embedding
Since the cokernel of (A.7) and ![]() ${\mathcal {O}}(G)[[h]]$ are both flat
${\mathcal {O}}(G)[[h]]$ are both flat ![]() $k[[h]]$-modules it follows that
$k[[h]]$-modules it follows that ![]() $\Lambda \otimes _{k[[h]]} {\mathcal {O}}(G)[[h]]$ is precisely the preimage of
$\Lambda \otimes _{k[[h]]} {\mathcal {O}}(G)[[h]]$ is precisely the preimage of ![]() $V[[h]] \otimes _{k[[h]]} ({\mathcal {O}}(G) \otimes _k {\mathcal {O}}(G))[[h]]$ under the composition (A.6).
$V[[h]] \otimes _{k[[h]]} ({\mathcal {O}}(G) \otimes _k {\mathcal {O}}(G))[[h]]$ under the composition (A.6).
Hence, it suffices to check that (A.6) carries ![]() $A( \Lambda )$ to
$A( \Lambda )$ to ![]() $V[[h]] \otimes _{k[[h]]} ({\mathcal {O}}(G) \otimes _k {\mathcal {O}}(G))[[h]]$. But the composition
$V[[h]] \otimes _{k[[h]]} ({\mathcal {O}}(G) \otimes _k {\mathcal {O}}(G))[[h]]$. But the composition
is equal to
by (A.5). Hence, it carries ![]() $\Lambda$ to
$\Lambda$ to ![]() $V[[h]] \otimes _{k[[h]]} ({\mathcal {O}}(G) \otimes _k {\mathcal {O}}(G))[[h]]$ and we win.
$V[[h]] \otimes _{k[[h]]} ({\mathcal {O}}(G) \otimes _k {\mathcal {O}}(G))[[h]]$ and we win.
Corollary A.3 There are no nontrivial homomorphisms from an affine group scheme to ![]() $L{\mathbb {G}}_m/L^+{\mathbb {G}}_m$.
$L{\mathbb {G}}_m/L^+{\mathbb {G}}_m$.
A.3 Subgroups of  $L\operatorname {PGL}(n)$
$L\operatorname {PGL}(n)$
Remark A.4 The analogous assertion for ![]() $L\operatorname {PGL}(n)$ does not hold.
$L\operatorname {PGL}(n)$ does not hold.
Consider the homomorphism of loop groups fpqc sheaves
induced by the projection ![]() $\operatorname {GL}(n) \to \operatorname {PGL}(n)$. We do not know if (A.9) is surjective as a morphism of fpqc sheaves. However, we shall see below that (A.9) is surjective over any affine group subscheme of
$\operatorname {GL}(n) \to \operatorname {PGL}(n)$. We do not know if (A.9) is surjective as a morphism of fpqc sheaves. However, we shall see below that (A.9) is surjective over any affine group subscheme of ![]() $L\operatorname {PGL}(n)$ of finite type over
$L\operatorname {PGL}(n)$ of finite type over ![]() $k$. For our applications we need a bit more general statement.
$k$. For our applications we need a bit more general statement.
Recall that an affine group scheme ![]() $H$ over a perfect field
$H$ over a perfect field ![]() $k$ is said to be pro-unipotent if there exists a filtration
$k$ is said to be pro-unipotent if there exists a filtration
by normal group subschemes such that
and every quotient ![]() $H/H^{\geq i}$ is unipotent (i.e. has a finite composition series with all quotient groups isomorphic to the additive group
$H/H^{\geq i}$ is unipotent (i.e. has a finite composition series with all quotient groups isomorphic to the additive group ![]() ${\mathbb {G}}_a$).
${\mathbb {G}}_a$).
Proposition A.5 Let ![]() $G$ be an affine group scheme over a perfect field
$G$ be an affine group scheme over a perfect field ![]() $k$, and let
$k$, and let ![]() $\phi : G \to L\operatorname {PGL}(n)$ be a homomorphism. Assume that
$\phi : G \to L\operatorname {PGL}(n)$ be a homomorphism. Assume that ![]() $G$ has a normal pro-unipotent group subscheme
$G$ has a normal pro-unipotent group subscheme ![]() $G^{\geq 1}\subset G$ such that
$G^{\geq 1}\subset G$ such that ![]() $\phi (G^{\geq 1})\subset L^+\operatorname {PGL}(n)$ and the quotient
$\phi (G^{\geq 1})\subset L^+\operatorname {PGL}(n)$ and the quotient ![]() $G_0=G/G^{\geq 1}$ has finite type over
$G_0=G/G^{\geq 1}$ has finite type over ![]() $k$. Then the following assertions hold.
$k$. Then the following assertions hold.
(i) The morphism of fpqc sheaves
 $\tilde {G}: = G \times _{L\operatorname {PGL}(n)} L\operatorname {GL}(n) \to G$ given by the projection to the first coordinate is surjective for the Zariski topology on
$\tilde {G}: = G \times _{L\operatorname {PGL}(n)} L\operatorname {GL}(n) \to G$ given by the projection to the first coordinate is surjective for the Zariski topology on  $G$ (and, consequently, for the fpqc topology).
$G$ (and, consequently, for the fpqc topology).(ii) The following two conditions are equivalent.
(1) There exists an element
 $g\in \operatorname {PGL}(n, k((h)))$ such that
$g\in \operatorname {PGL}(n, k((h)))$ such that  $\phi$ factors through
$\phi$ factors through  $gL^+\operatorname {PGL}(n)g^{-1}$:
$gL^+\operatorname {PGL}(n)g^{-1}$:
 \[ G\stackrel{\phi}{\longrightarrow} g(L^+\operatorname{PGL}(n)) g^{-1} \hookrightarrow L\operatorname{PGL}(n). \]
\[ G\stackrel{\phi}{\longrightarrow} g(L^+\operatorname{PGL}(n)) g^{-1} \hookrightarrow L\operatorname{PGL}(n). \]
(2) The extension
(A.10)admits a reduction \begin{equation} 1 \to L{\mathbb{G}}_m \to \tilde{G} \to G \to 1 \end{equation}
\begin{equation} 1 \to L{\mathbb{G}}_m \to \tilde{G} \to G \to 1 \end{equation} $\tilde {G} ^+$ to
$\tilde {G} ^+$ to  $L^+{\mathbb {G}}_m$ as follows.
$L^+{\mathbb {G}}_m$ as follows.

(iii) Assume that
 $G_0$ is smooth and connected. Then extension (A.10) admits a unique reduction
$G_0$ is smooth and connected. Then extension (A.10) admits a unique reduction  $\tilde {G} ^+$ to
$\tilde {G} ^+$ to  $L^+{\mathbb {G}}_m$.
$L^+{\mathbb {G}}_m$.
Proof. For part (i) observe that the morphism of schemes
admits a section locally for the Zariski topology on ![]() $L^+\operatorname {PGL}(n)$. Also since every
$L^+\operatorname {PGL}(n)$. Also since every ![]() $G^{\geq 1}$-torsor over an affine scheme is trivial the projection
$G^{\geq 1}$-torsor over an affine scheme is trivial the projection
admits a scheme-theoretic section ![]() $s: G_0 \to G$. Hence, it suffices to check that the composition
$s: G_0 \to G$. Hence, it suffices to check that the composition ![]() $G_0\stackrel {s}{\longrightarrow } G\stackrel {\phi }{\longrightarrow } L\operatorname {PGL}(n)$ lifts locally for the Zariski topology on
$G_0\stackrel {s}{\longrightarrow } G\stackrel {\phi }{\longrightarrow } L\operatorname {PGL}(n)$ lifts locally for the Zariski topology on ![]() $G_0$ to scheme-theoretic morphism
$G_0$ to scheme-theoretic morphism ![]() $G_0 \to L\operatorname {GL}(n)$. Set
$G_0 \to L\operatorname {GL}(n)$. Set ![]() $G_0 = \operatorname {Spec} R$. Then
$G_0 = \operatorname {Spec} R$. Then ![]() $\phi \circ s$ defines a morphism
$\phi \circ s$ defines a morphism
The pullback of the ![]() ${\mathbb {G}}_m$-torsor
${\mathbb {G}}_m$-torsor ![]() $\operatorname {GL}(n) \to \operatorname {PGL}(n)$ defines a
$\operatorname {GL}(n) \to \operatorname {PGL}(n)$ defines a ![]() ${\mathbb {G}}_m$-torsor
${\mathbb {G}}_m$-torsor ![]() $L$ over
$L$ over ![]() $\operatorname {Spec} R((h))$. Observe that
$\operatorname {Spec} R((h))$. Observe that ![]() $\phi \circ s$ admits a lifting to
$\phi \circ s$ admits a lifting to ![]() $L\operatorname {GL}(n)$ if and only if
$L\operatorname {GL}(n)$ if and only if ![]() $L$ is trivial. Thus, to complete the proof of part (i) we have to show that there exists an affine open covering
$L$ is trivial. Thus, to complete the proof of part (i) we have to show that there exists an affine open covering ![]() $\operatorname {Spec} R= \cup U_i$ such that the pullback of
$\operatorname {Spec} R= \cup U_i$ such that the pullback of ![]() $L$ to
$L$ to ![]() $\operatorname {Spec} {\mathcal {O}}(U_i)((h))$ is trivial for every
$\operatorname {Spec} {\mathcal {O}}(U_i)((h))$ is trivial for every ![]() $i$. We shall prove a stronger assertion: the morphism
$i$. We shall prove a stronger assertion: the morphism ![]() $\operatorname {Spec} R((h)) \to \operatorname {Spec} R$ induces an isomorphism
$\operatorname {Spec} R((h)) \to \operatorname {Spec} R$ induces an isomorphism
Since ![]() $G_0$ is a group scheme and
$G_0$ is a group scheme and ![]() $k$ is perfect, the reduction
$k$ is perfect, the reduction ![]() $R_{\rm red}$ is smooth over
$R_{\rm red}$ is smooth over ![]() $k$. Since
$k$. Since ![]() $R$ is a finitely generated
$R$ is a finitely generated ![]() $k$-algebra, the kernel of the projection
$k$-algebra, the kernel of the projection ![]() $R \to R_{\rm red}$ is a nilpotent ideal. It follows that
$R \to R_{\rm red}$ is a nilpotent ideal. It follows that ![]() $( R((h))_{\rm red} \buildrel {\sim }\over {\longrightarrow } R_{\rm red}((h))$. Consequently, we have that
$( R((h))_{\rm red} \buildrel {\sim }\over {\longrightarrow } R_{\rm red}((h))$. Consequently, we have that
Next, using regularity of ![]() $R_{\rm red}((h))$ we conclude that
$R_{\rm red}((h))$ we conclude that
This proves part (i).
For part (ii), let ![]() $\tilde {G} ^+$ be a reduction of
$\tilde {G} ^+$ be a reduction of ![]() $\tilde {G}$ to
$\tilde {G}$ to ![]() $L^+{\mathbb {G}}_m$. Since
$L^+{\mathbb {G}}_m$. Since ![]() $L^+{\mathbb {G}}_m$ is an affine group scheme (as opposed to merely a group ind-scheme)
$L^+{\mathbb {G}}_m$ is an affine group scheme (as opposed to merely a group ind-scheme) ![]() $\tilde {G} ^+$ is also an affine group scheme. Applying Proposition A.2 we conclude that the homomorphism
$\tilde {G} ^+$ is also an affine group scheme. Applying Proposition A.2 we conclude that the homomorphism ![]() $\tilde {G} ^+ \to L\operatorname {GL}(n)$ factors through
$\tilde {G} ^+ \to L\operatorname {GL}(n)$ factors through ![]() $gL^+ \operatorname {GL}(n)g^{-1}$, for some
$gL^+ \operatorname {GL}(n)g^{-1}$, for some ![]() $g\in \operatorname {GL}(n, k((h)))$. Hence,
$g\in \operatorname {GL}(n, k((h)))$. Hence, ![]() $G \to L\operatorname {PGL}(n)$ factors through
$G \to L\operatorname {PGL}(n)$ factors through ![]() $gL^+\operatorname {PGL}(n)g^{-1}$. The inverse implication is clear.
$gL^+\operatorname {PGL}(n)g^{-1}$. The inverse implication is clear.
Finally, for part (iii), set ![]() $\bar {G}:= \tilde {G} / L^+{\mathbb {G}}_m$. We have to show that the central extension
$\bar {G}:= \tilde {G} / L^+{\mathbb {G}}_m$. We have to show that the central extension
admits a unique splitting. We shall first construct a scheme-theoretic section of the projection ![]() $\bar {G} \to G$. Using part (i) there exists an open cover
$\bar {G} \to G$. Using part (i) there exists an open cover ![]() $G= \cup U_i$ and sections
$G= \cup U_i$ and sections ![]() $s_i: U_i \to \tilde {G}$ of the projection
$s_i: U_i \to \tilde {G}$ of the projection ![]() $\tilde {G} \to G$. Let
$\tilde {G} \to G$. Let ![]() $\bar {s}_i: U_i \to \bar {G}$ be the composition of
$\bar {s}_i: U_i \to \bar {G}$ be the composition of ![]() $s_i$ with the quotient map
$s_i$ with the quotient map ![]() $\tilde {G} \to \bar {G}$. Since
$\tilde {G} \to \bar {G}$. Since ![]() $G$ is reduced the morphisms
$G$ is reduced the morphisms
lands at the second factor. Hence the collection ![]() $\{\bar {s}_i \bar {s}_j^{-1}\}$ defines a Čech
$\{\bar {s}_i \bar {s}_j^{-1}\}$ defines a Čech ![]() $1$-cocycle for the constant sheaf
$1$-cocycle for the constant sheaf ![]() ${\mathbb {Z}}$ on
${\mathbb {Z}}$ on ![]() $G$. Since
$G$. Since ![]() $G$ is irreducible, we have that
$G$ is irreducible, we have that ![]() $\check {H}^{1}(G, \mathbb {Z})=0$. Thus, we have a global scheme-theoretic section
$\check {H}^{1}(G, \mathbb {Z})=0$. Thus, we have a global scheme-theoretic section ![]() $\bar {s}: G \to \bar {G}$ of the projection
$\bar {s}: G \to \bar {G}$ of the projection ![]() $\bar G \to G$. We claim that every such section satisfying
$\bar G \to G$. We claim that every such section satisfying ![]() $\bar {s}(1) =1$ is a group homomorphism. To see this it suffices to show that the following diagram is commutative.
$\bar {s}(1) =1$ is a group homomorphism. To see this it suffices to show that the following diagram is commutative.

In turn, this follows from the fact that every scheme-theoretic morphism from a connected reduced scheme to ![]() $\operatorname {Gr}_{\mathbb {G}_m}$ is constant.
$\operatorname {Gr}_{\mathbb {G}_m}$ is constant.
A.4 A representation of  $\operatorname {\mathfrak {sp}}(2n)$
$\operatorname {\mathfrak {sp}}(2n)$
In this subsection we prove irreducibility of a certain representation of the Lie algebra ![]() $\operatorname {\mathfrak {sp}}(2n)$ that we used in the proof of Lemma 4.3. We use notation from § 4.1.
$\operatorname {\mathfrak {sp}}(2n)$ that we used in the proof of Lemma 4.3. We use notation from § 4.1.
Lemma A.6 For every integer ![]() $l$ with
$l$ with ![]() $0\leq l < 2(p-1)$, the adjoint representation of the Lie algebra
$0\leq l < 2(p-1)$, the adjoint representation of the Lie algebra ![]() $\operatorname {\mathfrak {sp}}(2n) = m^2/m^3$ on
$\operatorname {\mathfrak {sp}}(2n) = m^2/m^3$ on ![]() $m^l/m^{l+1}$ is irreducible.
$m^l/m^{l+1}$ is irreducible.
Proof. Write ![]() $m_n^l / m_n^{l+1}$ for
$m_n^l / m_n^{l+1}$ for ![]() $m^k / m^{k+1}$. It is easy to verify the assertion of the lemma for
$m^k / m^{k+1}$. It is easy to verify the assertion of the lemma for ![]() $n=1$: in fact, the representation of
$n=1$: in fact, the representation of ![]() $\operatorname {\mathfrak {sp}}(2)= m_1/m_1^2$ on
$\operatorname {\mathfrak {sp}}(2)= m_1/m_1^2$ on ![]() $m_1^l / m_1^{l+1}$ is irreducible for every
$m_1^l / m_1^{l+1}$ is irreducible for every ![]() $l\geq 0$. Moreover, the representations
$l\geq 0$. Moreover, the representations ![]() $m_1^l / m_1^{l+1}$ and
$m_1^l / m_1^{l+1}$ and ![]() $m_1^{l'} / m_1^{l'+1}$ are isomorphic if and only if
$m_1^{l'} / m_1^{l'+1}$ are isomorphic if and only if ![]() $l+l' =2p-2$.
$l+l' =2p-2$.
To prove the lemma in general, consider the restriction of the representation of ![]() $\operatorname {\mathfrak {sp}}(2n)$ on
$\operatorname {\mathfrak {sp}}(2n)$ on ![]() $m_n^l / m_n^{l+1}$ to the Lie subalgebra
$m_n^l / m_n^{l+1}$ to the Lie subalgebra
of the block diagonal matrices. The latter representation decomposes as follows:
By the Jacobson density theorem the representation of ![]() $\operatorname {\mathfrak {sp}}(2)^{\oplus ^n}$ on each summand is irreducible. Moreover, if
$\operatorname {\mathfrak {sp}}(2)^{\oplus ^n}$ on each summand is irreducible. Moreover, if ![]() $l< 2(p-1)$, then these direct summands are pairwise nonisomorphic. It follows that any subspace
$l< 2(p-1)$, then these direct summands are pairwise nonisomorphic. It follows that any subspace ![]() $V\subset m^l_n/m_n^{l+1}$ invariant under the
$V\subset m^l_n/m_n^{l+1}$ invariant under the ![]() $\operatorname {\mathfrak {sp}}(2)^{\oplus ^n}$-action is the sum of some of the summands appearing in (A.13). Hence, it suffices to prove that if a
$\operatorname {\mathfrak {sp}}(2)^{\oplus ^n}$-action is the sum of some of the summands appearing in (A.13). Hence, it suffices to prove that if a ![]() $\operatorname {\mathfrak {sp}}(2n)$-subrepresentation
$\operatorname {\mathfrak {sp}}(2n)$-subrepresentation ![]() $W \subset m^l_n/m_n^{l+1}$ contains
$W \subset m^l_n/m_n^{l+1}$ contains ![]() $m_1^{i_1} / m_1^{i_1 + 1} \otimes \cdots \otimes m_1^{i_n} / m_1^{i_n + 1}$, for some partition
$m_1^{i_1} / m_1^{i_1 + 1} \otimes \cdots \otimes m_1^{i_n} / m_1^{i_n + 1}$, for some partition ![]() $(i_1, \ldots, i_n)$ of
$(i_1, \ldots, i_n)$ of ![]() $l$ with
$l$ with ![]() $i_1>0$, the projection of
$i_1>0$, the projection of ![]() $W$ to
$W$ to ![]() $m_1^{i_1-1} / m_1^{i_1} \otimes m_1^{i_2+1} / m_1^{i_2+2} \otimes \cdots \otimes m_1^{i_n} / m_1^{i_n + 1}$ is nonzero. This reduces the proof to the case
$m_1^{i_1-1} / m_1^{i_1} \otimes m_1^{i_2+1} / m_1^{i_2+2} \otimes \cdots \otimes m_1^{i_n} / m_1^{i_n + 1}$ is nonzero. This reduces the proof to the case ![]() $n=2$ which is shown by direct inspection.
$n=2$ which is shown by direct inspection.