Article contents
On p-adic uniformization of abelian varieties with good reduction
Published online by Cambridge University Press: 05 September 2022
Abstract
Let 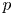 $p$ be a rational prime, let
$p$ be a rational prime, let 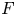 $F$ denote a finite, unramified extension of
$F$ denote a finite, unramified extension of 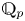 ${{\mathbb {Q}}}_p$, let
${{\mathbb {Q}}}_p$, let 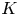 $K$ be the maximal unramified extension of
$K$ be the maximal unramified extension of 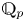 ${{\mathbb {Q}}}_p$,
${{\mathbb {Q}}}_p$, 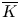 ${{\overline {K}}}$ some fixed algebraic closure of
${{\overline {K}}}$ some fixed algebraic closure of 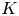 $K$, and
$K$, and 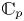 ${{\mathbb {C}}}_p$ be the completion of
${{\mathbb {C}}}_p$ be the completion of 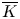 ${{\overline {K}}}$. Let
${{\overline {K}}}$. Let 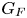 $G_F$ be the absolute Galois group of
$G_F$ be the absolute Galois group of 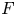 $F$. Let
$F$. Let 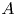 $A$ be an abelian variety defined over
$A$ be an abelian variety defined over 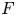 $F$, with good reduction. Classically, the Fontaine integral was seen as a Hodge–Tate comparison morphism, i.e. as a map
$F$, with good reduction. Classically, the Fontaine integral was seen as a Hodge–Tate comparison morphism, i.e. as a map 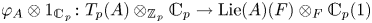 $\varphi _{A} \otimes 1_{{{\mathbb {C}}}_p}\colon T_p(A)\otimes _{{{\mathbb {Z}}}_p}{{\mathbb {C}}}_p\to \operatorname {Lie}(A)(F)\otimes _F{{\mathbb {C}}}_p(1)$, and as such it is surjective and has a large kernel. This paper starts with the observation that if we do not tensor
$\varphi _{A} \otimes 1_{{{\mathbb {C}}}_p}\colon T_p(A)\otimes _{{{\mathbb {Z}}}_p}{{\mathbb {C}}}_p\to \operatorname {Lie}(A)(F)\otimes _F{{\mathbb {C}}}_p(1)$, and as such it is surjective and has a large kernel. This paper starts with the observation that if we do not tensor 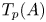 $T_p(A)$ with
$T_p(A)$ with 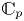 ${{\mathbb {C}}}_p$, then the Fontaine integral is often injective. In particular, it is proved that if
${{\mathbb {C}}}_p$, then the Fontaine integral is often injective. In particular, it is proved that if 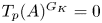 $T_p(A)^{G_K} = 0$, then
$T_p(A)^{G_K} = 0$, then 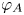 $\varphi _A$ is injective. As an application, we extend the Fontaine integral to a perfectoid like universal cover of
$\varphi _A$ is injective. As an application, we extend the Fontaine integral to a perfectoid like universal cover of 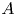 $A$ and show that if
$A$ and show that if 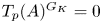 $T_p(A)^{G_K} = 0$, then
$T_p(A)^{G_K} = 0$, then 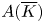 $A(\overline {K})$ has a type of
$A(\overline {K})$ has a type of 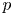 $p$-adic uniformization, which resembles the classical complex uniformization.
$p$-adic uniformization, which resembles the classical complex uniformization.
- Type
- Research Article
- Information
- Copyright
- © 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
With an appendix by Yeuk Hay Joshua Lam and Alexander Petrov
References
- 3
- Cited by



