Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T16:51:11.097Z Has data issue: false hasContentIssue false
  • English
  • Français

On number fields with given ramification

Part of: Discontinuous groups and automorphic forms Algebraic number theory: global fields

Published online by Cambridge University Press:  01 November 2007

Gaëtan Chenevier
Gaëtan Chenevier*
Affiliation:
Institut Galilée LAGA, Université Paris 13, 99 Avenue J-B. Clément, 93430 Villetaneuse, France (email: [email protected], [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E be a CM number field and let S be a finite set of primes of E containing the primes dividing a given prime number l and another prime u split above the maximal totally real subfield of E. If ES denotes a maximal algebraic extension of E which is unramified outside S, we show that the natural maps 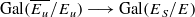are injective. We discuss generalizations of this result.

Keywords

global Galois groupsrestricted ramificationautomorphic forms

MSC classification

Secondary: 11F55: Other groups and their modular and automorphic forms (several variables) 11F80: Galois representations 11R32: Galois theory
Type
Research Article
Information
Compositio Mathematica , Volume 143 , Issue 6 , November 2007 , pp. 1359 - 1373
Copyright
Copyright © Foundation Compositio Mathematica 2007

References

The author is supported by the C.N.R.S.