Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T05:45:39.586Z Has data issue: false hasContentIssue false
  • English
  • Français

On monic abelian cubics

Part of: Forms and linear algebraic groups Arithmetic algebraic geometry Algebraic number theory: global fields Polynomials and matrices

Published online by Cambridge University Press:  16 May 2022

Stanley Yao Xiao
Stanley Yao Xiao*
Affiliation:
Department of Mathematics, University of Toronto, Bahen Centre, Toronto, ON, Canada M5S 2E4 [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove the assertion that the number of monic cubic polynomials 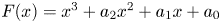$F(x) = x^3 + a_2 x^2 + a_1 x + a_0$ with integer coefficients and irreducible, Galois over 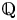${\mathbb {Q}}$ satisfying 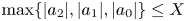$\max \{|a_2|, |a_1|, |a_0|\} \leq X$ is bounded from above by 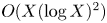$O(X (\log X)^2)$. We also count the number of abelian monic binary cubic forms with integer coefficients up to a natural equivalence relation ordered by the so-called Bhargava–Shankar height. Finally, we prove an assertion characterizing the splitting field of 2-torsion points of semi-stable abelian elliptic curves.

Keywords

Galois theorycubic polynomials

MSC classification

Primary: 11R32: Galois theory
Secondary: 11R45: Density theorems 11C08: Polynomials 11E76: Forms of degree higher than two 11G05: Elliptic curves over global fields
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 3 , March 2022 , pp. 550 - 567
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author thanks S. Chow for several important discussions which contributed enormously to the paper, and M. Widmer for some helpful comments.

References

Bhargava, M., Higher composition laws I: a new view on Gauss composition, and quadratic generalizations, Ann. of Math. 159 (2004), 217–250.CrossRefGoogle Scholar
Bhargava, M., Galois groups of random integer polynomials and van der Waerden's Conjecture, Preprint (2021), arXiv:2111.06507 [math.NT].Google Scholar
Bhargava, M. and Shankar, A., Binary quartic forms having bounded invariants, and the boundedness of the average rank of elliptic curves, Ann. of Math. (2) 181 (2015), 191–242.10.4007/annals.2015.181.1.3CrossRefGoogle Scholar
Bhargava, M. and Shnidman, A., On the number of cubic orders of bounded discriminant having automorphism group $C_3$, and related problems, Algebra Number Theory, (1) 8 (2014), 53–88.10.2140/ant.2014.8.53CrossRefGoogle Scholar
Brookfield, G., Factoring forms, Amer. Math. Monthly 123 (2016), 347–362.10.4169/amer.math.monthly.123.4.347CrossRefGoogle Scholar
Chow, S. and Dietmann, R., Enumerative Galois theory for cubics and quartics, Adv. Math. 372 (2020), 1–37.10.1016/j.aim.2020.107282CrossRefGoogle Scholar
Chow, S. and Dietmann, R., Towards van der Waerden's conjecture, Preprint (2021), arXiv:2106.14593 [math.NT].Google Scholar
Cohen, H., Number theory – volume II: analytic and modern tools, Graduate Texts in Mathematics, vol. 240 (Springer, New York, 2007).Google Scholar
Heath-Brown, D. R., Square-free values of $n^2 + 1$, Acta Arith. 155 (2012), 1–13.CrossRefGoogle Scholar
Hooley, C., On binary cubic forms: II, J. Reine Angew. Math. 521 (2000), 185–240.Google Scholar
Lefton, P., On the Galois groups of cubics and trinomials, Acta Arith. 35 (1979), 239–246.CrossRefGoogle Scholar
Smith, G. W., Some polynomials over ${\mathbb {Q}}(t)$ and their Galois groups, Math. Comp. 69 (1999), 775–796.10.1090/S0025-5718-99-01160-6CrossRefGoogle Scholar
Stewart, C. L., On the number of solutions of polynomial congruences and Thue equations, J. Amer. Math. Soc. (4) 4 (1991), 793–835.CrossRefGoogle Scholar
van der Waerden, B. L., Die Seltenheit der reduziblen Gleichungen und die Gleichungen mit Affekt, Monatsh. Math. 43 (1936), 137–147.Google Scholar
Weisstein, E. W., Cubic formula. From MathWorld—A Wolfram web resource. https://mathworld.wolfram.com/CubicFormula.html.Google Scholar
Xiao, S. Y., On binary cubic and quartic forms, J. Théor. Nombres Bordeaux 31 (2019), 323–341.CrossRefGoogle Scholar
Yu, G., Average size of 2-selmer groups of elliptic curves, I, Trans. Amer. Math. Soc. 358 (2006), 1563–1584.CrossRefGoogle Scholar