Hostname: page-component-6bf8c574d5-pdxrj Total loading time: 0 Render date: 2025-03-08T05:13:02.906Z Has data issue: false hasContentIssue false
  • English
  • Français

On a purely inseparable analogue of the Abhyankar conjecture for affine curves

Part of: Affine geometry Algebraic groups Curves

Published online by Cambridge University Press:  19 July 2018

Shusuke Otabe
Shusuke Otabe*
Affiliation:
Mathematical Institute, Graduate School of Science, Tohoku University, 6-3 Aramakiaza, Aoba, Sendai, Miyagi 980-8578, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 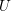$U$ be an affine smooth curve defined over an algebraically closed field of positive characteristic. The Abhyankar conjecture (proved by Raynaud and Harbater in 1994) describes the set of finite quotients of Grothendieck’s étale fundamental group 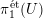$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$. In this paper, we consider a purely inseparable analogue of this problem, formulated in terms of Nori’s profinite fundamental group scheme 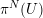$\unicode[STIX]{x1D70B}^{N}(U)$, and give a partial answer to it.

Keywords

fundamental group schemestorsorsinverse Galois problem

MSC classification

Primary: 14L15: Group schemes 14R20: Group actions on affine varieties 14H30: Coverings, fundamental group
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 8 , August 2018 , pp. 1633 - 1658
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by JSPS, Grant-in-Aid for Scientific Research for JSPS fellows (16J02171).

References

Abhyankar, S., Coverings of algebraic curves , Amer. J. Math. 79 (1957), 825–856.Google Scholar
Abhyankar, S., Galois theory on the line in nonzero characteristic , Bull. Amer. Math. Soc. (N.S.) 27 (1992), 68–133.Google Scholar
Abramovich, D., Olsson, M. and Vistoli, A., Tame stacks in positive characteristic , Ann. Inst. Fourier (Grenoble) 58 (2008), 1057–1091.Google Scholar
Antei, M., On the abelian fundamental group scheme of a family of varieties , Israel J. Math. 186 (2011), 427–446.Google Scholar
Borne, N., Sur les représentations du groupe fondamental d’une variété privée d’un diviseur à croisements normaux simples , Indiana Univ. Math. J. 58 (2009), 137–180.Google Scholar
Borne, N. and Vistoli, A., The Nori fundamental gerbe of a fibered category , J. Algebr. Geom. 24 (2015), 311–353.Google Scholar
Bouw, I. I., The p-rank of curves and covers of curves , in Courbes semi-stables et groupe fondamental en géométrie algébrique (Luminy, 1998), Progress in Mathematics, vol. 187 (Birkhäuser, Basel, 2000), 267–277.Google Scholar
Chinburg, T., Erez, B., Pappas, G. and Taylor, M. J., Tame actions of group schemes: integrals and slices , Duke Math. J. 82 (1996), 269–308.Google Scholar
Deligne, P., Catégories tannakiennes , in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser Boston, Boston, MA, 1990), 111–195.Google Scholar
Deligne, P. and Milne, J., Tannakian categories, Lectures Notes in Mathematics, vol. 900 (Springer, Berlin–New York, 1982).Google Scholar
Esnault, H., Hai, P. H. and Sun, X., On Nori’s fundamental group scheme , in Geometry and dynamics of groups and spaces, Progress in Mathematics, vol. 265 (Birkhäuser, Basel, 2008), 377–398.Google Scholar
Esnault, H. and Hogadi, A., On the algebraic fundamental group of smooth varieties in characteristic p > 0 , Trans. Amer. Math. Soc. 364 (2012), 2429–2442.+0+,+Trans.+Amer.+Math.+Soc.+364+(2012),+2429–2442.>Google Scholar
Fried, M. D. and Jarden, M., Field arithmetic , in Ergebnisse der Mathematik und ihrer Grenzgebiete (3), A Series of Modern Surveys in Mathematics, vol. 11, third edition (Springer, Berlin, 2008).Google Scholar
Gieseker, D., Flat vector bundles and the fundamental group in non-zero characteristics , Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 2 (1975), 1–31.Google Scholar
Gillibert, J., Tame stacks and log flat torsors, Preprint (2012), arXiv:1203.6870v1.Google Scholar
Giraud, J., Cohomologie non abélienne , in Die Grundlehren der mathematischen Wissenschaften, Band, vol. 179 (Springer, Berlin–New York, 1971).Google Scholar
Harbater, D., Abhyankar’s conjecture on Galois groups over curves , Invent. Math. 117 (1994), 1–25.Google Scholar
Harbater, D., Obus, A., Pries, R. and Stevenson, K., Abhyankar’s conjectures in Galois theory: current status and future directions , Bull. Amer. Math. Soc. (N.S.) 55 (2018), 239–287.Google Scholar
Jantzen, J. C., Representations of algebraic groups, Mathematical Surveys and Monographs, vol. 107, second edition (American Mathematical Society, Providence, RI, 2003).Google Scholar
Jouanolou, J.-P., Théorèmes de Bertini et applications, Progress in Mathematics, vol. 42 (Birkhäuser, Boston, MA, 1983).Google Scholar
Kambayashi, T., Nori’s construction of Galois coverings in positive characteristics, Algebraic and Topological Theories (Kinosaki, 1984), (Kinokuniya, Tokyo, 1986), 640–647.Google Scholar
Lam, T. Y., Serre’s conjecture, Lecture Notes in Mathematics, vol. 635 (Springer, Berlin–New York, 1978).Google Scholar
Marques, S., Actions modérées de schémas en groupes affines et champs modérés , C. R. Math. Acad. Sci. Paris 350 (2012), 125–128.Google Scholar
Mumford, D., Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics, vol. 5, (Published by the Tata Institute of Fundamental Research, Bombay by Hindustan Book Agency, New Delhi, 2008).Google Scholar
Nori, M. V., On the representations of the fundamental group , Compositio Math. 33 (1976), 29–41.Google Scholar
Nori, M. V., The fundamental group-scheme , Proc. Indian Acad. Sci. Math. Sci. 91 (1982), 73–122.Google Scholar
Nori, M. V., Unramified coverings of the affine line in positive characteristic , in Algebraic geometry and its applications (West Lafayette, IN, 1990) (Springer, New York, 1994), 209–212.Google Scholar
Pacheco, A. and Stevenson, K. F., Finite quotients of the algebraic fundamental group of projective curves in positive characteristic , Pacific J. Math. 192 (2000), 143–158.Google Scholar
Raynaud, M., Revêtements de la droite affine en caractéristique p > 0 et conjecture d’Abhyankar , Invent. Math. 116 (1994), 425–462.+0+et+conjecture+d’Abhyankar+,+Invent.+Math.+116+(1994),+425–462.>Google Scholar
dos Santos, J. P. P., Fundamental group schemes for stratified sheaves , J. Algebra 317 (2007), 691–713.Google Scholar
Serre, J.-P., Construction de revêtements étales de la droite affine en caractéristique p , C. R. Acad. Sci. Paris Sér. I Math. 311 (1990), 341–346.Google Scholar
Serre, J.-P., Revêtements de courbes algébriques , in Séminaire Bourbaki, Vol. 1991/92, Astérisque, No. 206, Exp. No. 749, 3, (1992), 167–182.Google Scholar
Grothendieck, A., Revêtements étales et groupe fondamental (SGA1), Lecture Notes in Mathematics, vol. 224 (Springer, Berlin–New York, 1971).Google Scholar
Tamagawa, A., On the fundamental groups of curves over algebraically closed fields of characteristic > 0 , Int. Math. Res. Not. (IMRN) 1999 (1999), 853–873.+0+,+Int.+Math.+Res.+Not.+(IMRN)+1999+(1999),+853–873.>Google Scholar
Tamagawa, A., Finiteness of isomorphism classes of curves in positive characteristic with prescribed fundamental groups , J. Algebraic Geom. 13 (2004), 675–724.Google Scholar
The Stacks Project Authors, Stacks Project, https://stacks.math.columbia.edu.Google Scholar
Ünver, S., On the local unipotent fundamental group scheme , Canad. Math. Bull. 53 (2010), 187–191.Google Scholar
Waterhouse, W. C., Introduction to affine group schemes, Graduate Texts in Mathematics, vol. 66 (Springer, New York–Berlin, 1979).Google Scholar
Zalamansky, G., Ramification of inseparable coverings of schemes and application to diagonalizable group actions, Preprint (2016), arXiv:1603.09284v1.Google Scholar
Zhang, L., The homotopy sequence of Nori’s fundamental group , J. Algebra 393 (2013), 79–91.Google Scholar