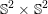Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kennard, Lee
2017.
Fundamental Groups of Manifolds with Positive Sectional Curvature and Torus Symmetry.
The Journal of Geometric Analysis,
Vol. 27,
Issue. 4,
p.
2894.
Amann, Manuel
and
Kennard, Lee
2020.
Positive curvature and symmetry in small dimensions.
Communications in Contemporary Mathematics,
Vol. 22,
Issue. 06,
p.
1950053.
Amann, Manuel
2021.
Bounds on Sectional Curvature and Interactions with Topology.
Jahresbericht der Deutschen Mathematiker-Vereinigung,
Vol. 123,
Issue. 1,
p.
27.
Seck, Thierno
Niang, Athoumane
and
Masiello, Antonio
2022.
Conformal Metrics to a Product or Doubly Warped Product on S2×S2 and the Hopf Conjecture.
Journal of Mathematics,
Vol. 2022,
Issue. 1,