Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T09:48:44.478Z Has data issue: false hasContentIssue false
  • English
  • Français

On a completed generating function of locally harmonic Maass forms

Part of: Forms and linear algebraic groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  26 March 2014

Kathrin Bringmann ,
Ben Kane  and
Sander Zwegers
Kathrin Bringmann
Affiliation:
Mathematical Institute, University of Cologne, Weyertal 86-90, 50931 Cologne, Germany email [email protected]
Ben Kane
Affiliation:
Mathematical Institute, University of Cologne, Weyertal 86-90, 50931 Cologne, Germany email [email protected]
Sander Zwegers
Affiliation:
Mathematical Institute, University of Cologne, Weyertal 86-90, 50931 Cologne, Germany email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

While investigating the Doi–Naganuma lift, Zagier defined integral weight cusp forms 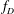$f_D$ which are naturally defined in terms of binary quadratic forms of discriminant 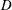$D$. It was later determined by Kohnen and Zagier that the generating function for the function 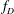$f_D$ is a half-integral weight cusp form. A natural preimage of 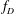$f_D$ under a differential operator at the heart of the theory of harmonic weak Maass forms was determined by the first two authors and Kohnen. In this paper, we consider the modularity properties of the generating function of these preimages. We prove that although the generating function is not itself modular, it can be naturally completed to obtain a half-integral weight modular object.

Keywords

locally harmonic Maass formsindefinite theta functionsholomorphic projectionmock modular formsmodular forms

MSC classification

Secondary: 11F27: Theta series; Weil representation; theta correspondences 11F25: Hecke-Petersson operators, differential operators (one variable) 11F37: Forms of half-integer weight; nonholomorphic modular forms 11E16: General binary quadratic forms 11F11: Holomorphic modular forms of integral weight
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 5 , May 2014 , pp. 749 - 762
Copyright
© The Author(s) 2014 

References

Andrews, G., Partitions, Durfee symbols, and the Atkin–Garvan moments of ranks, Invent. Math. 169 (2007), 37–73.Google Scholar
Bringmann, K., On the explicit construction of higher deformations of partition statistics, Duke Math. J. 144 (2008), 195–233.CrossRefGoogle Scholar
Bringmann, K., Garvan, F. and Mahlburg, K., Partition statistics and quasiharmonic Maass forms, Int. Math. Res. Not. 2009 (2009), 63–97.Google Scholar
Bringmann, K., Kane, B. and Kohnen, W., Locally harmonic Maass forms and rational period functions, Preprint (2012), arXiv:1206.1100v2.Google Scholar
Bringmann, K. and Ono, K., The f (q) mock theta function conjecture and partition ranks, Invent. Math. 165 (2006), 243–266.CrossRefGoogle Scholar
Bringmann, K. and Ono, K., Arithmetic properties of coefficients of half-integral weight Maass–Poincaré series, Math. Ann. 337 (2007), 591–612.Google Scholar
Bringmann, K. and Ono, K., Dyson’s ranks and Maass forms, Ann. of Math. (2) 171 (2010), 419–449.Google Scholar
Bruinier, J., Funke, J. and Imamoḡlu, Ö., Regularized theta liftings and periods of modular functions, J. Reine Angew. Math., to appear.Google Scholar
Bruinier, J., Funke, J. and Imamoḡlu, Ö., Rational period functions, singular automorphic forms, and theta lifts, in preparation.Google Scholar
Bruinier, J. and Ono, K., Heegner divisors, L-functions, and Maass forms, Ann. of Math. (2) 172 (2010), 2135–2181.Google Scholar
Bruinier, J. and Yang, T., Faltings heights of CM cycles and derivatives of L-functions, Invent. Math. 177 (2009), 631–681.CrossRefGoogle Scholar
Doi, K. and Naganuma, H., On the algebraic curves uniformized by arithmetical automorphic functions, Ann. of Math. (2) 86 (1967), 449–460.CrossRefGoogle Scholar
Eguchi, T., Ooguri, H. and Tachikawa, Y., Notes on the K3 surface and the Mathieu group M 24, Experiment. Math. 20 (2011), 91–96.CrossRefGoogle Scholar
Klingen, H., Introductory lectures on Siegel modular forms (Cambridge University Press, Cambridge, 1990).Google Scholar
Kohnen, W. and Zagier, D., Values of L-series of modular forms at the center of the critical strip, Invent. Math. 64 (1981), 175–198.Google Scholar
Lipschitz, R., Untersuchung der Eigenschaften einer Gattung von unendlichen Reihen, J. Reine Angew. Math. 105 (1889), 127–156.Google Scholar
Ono, K., Unearthing the visions of a master: harmonic Maass forms and number theory, in Proceedings of the 2008 Harvard–MIT Current Developments in Mathematics Conference (International Press, Somerville, MA, 2009), 347–454.Google Scholar
Shintani, T., On construction of holomorphic cusp forms of half integral weight, Nagoya Math. J. 58 (1975), 83–126.Google Scholar
Sturm, J., Projections of C ∞ automorphic forms, Bull. Amer. Math. Soc. 2 (1980), 435–439.Google Scholar
Vignéras, M., Séries theta des formes quadratiques indéfinies, in Modular functions of one variable VI, Lecture Notes in Mathematics, vol. 627 (Springer, Berlin, 1977), 227–239.CrossRefGoogle Scholar
Zagier, D., Modular forms associated to real quadratic fields, Invent. Math. 30 (1975), 1–46.Google Scholar
Zagier, D., The Eichler–Selberg trace formula on SL2(ℤ), in Appendix to S. Lang, Introduction to modular forms, Grundlehren der Mathematischen Wissenschaften, vol. 222 (Springer, Berlin, 1976), 44–54.Google Scholar
Zagier, D., Introduction to modular forms: from number theory to physics (Springer, Berlin, 1992), 238–291.Google Scholar
Zagier, D., Traces of singular moduli, in Motives, polylogarithms and Hodge theory, part I, International Press Lecture Series, eds Bogomolov, F. and Katzarkov, L. (International Press, Somervile, MA, 2002), 211–244.Google Scholar
Zagier, D., The Mellin transform and other useful analytic techniques, in Appendix to E. Zeidler, Quantum field theory I: basics in mathematics and physics (Springer, Berlin, 2006), 305–323.Google Scholar
Zagier, D., Ramanujan’s mock theta functions and their applications, Astérique 326 (2009), 143–164.Google Scholar
Zwegers, S., Mock theta functions, PhD thesis, Utrecht University (2002).Google Scholar