Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-16T18:44:42.569Z Has data issue: false hasContentIssue false
  • English
  • Français

Obstruction theory and the level n elliptic genus

Part of: Operations and obstructions Homotopy theory Homology and cohomology theories

Published online by Cambridge University Press:  03 August 2023

Andrew Senger
Andrew Senger*
Affiliation:
Department of Mathematics, Harvard University, 1 Oxford Street, Cambridge, MA 02138, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a height at most two Landweber exact $\mathbb {E}_\infty$-ring $E$ whose homotopy is concentrated in even degrees, we show that any complex orientation of $E$ which satisfies the Ando criterion admits a unique lift to an 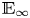$\mathbb {E}_\infty$-complex orientation 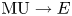$\mathrm {MU} \to E$. As a consequence, we give a short proof that the level 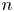$n$ elliptic genus lifts uniquely to an 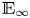$\mathbb {E}_\infty$-complex orientation $\mathrm {MU} \to \mathrm {tmf}_1 (n)$ for all 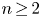$n\, {\geq}\, 2$.

Keywords

topological modular formscomplex orientationobstruction theory

MSC classification

Primary: 55N34: Elliptic cohomology 55P43: Spectra with additional structure ($E_infty$, $A_infty$, ring spectra, etc.) 55S35: Obstruction theory
Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 9 , September 2023 , pp. 2000 - 2021
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

During the course of this work, the author was supported by NSF Grants DGE-1745302 and DMS-2103236.

References

Absmeier, D., Strictly commutative complex orientations of $Tmf_1 (N)$, Preprint (2021), arXiv:2108.03079.Google Scholar
Adams, J. F., Stable homotopy and generalised homology, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 1974).Google Scholar
Ando, M., Blumberg, A. J., Gepner, D., Hopkins, M. J. and Rezk, C., Units of ring spectra, orientations and Thom spectra via rigid infinite loop space theory, J. Topol. 7 (2014), 1077–1117.CrossRefGoogle Scholar
Ando, M., Hopkins, M. J. and Rezk, C., Multiplicative orientations of $KO$-theory and of the spectrum of topological modular forms, Preprint (2010), https://faculty.math.illinois.edu/~mando/papers/koandtmf.pdf.Google Scholar
Ando, M., Hopkins, M. J. and Strickland, N. P., Elliptic spectra, the Witten genus and the theorem of the cube, Invent. Math. 146 (2001), 595–687.CrossRefGoogle Scholar
Ando, M., Hopkins, M. J. and Strickland, N. P., The sigma orientation is an $H_\infty$ map, Amer. J. Math. 126 (2004), 247–334.CrossRefGoogle Scholar
Arone, G. and Lesh, K., Filtered spectra arising from permutative categories, J. Reine Angew. Math. 604 (2007), 73–136.Google Scholar
Atiyah, M. F., Bott, R. and Shapiro, A., Clifford modules, Topology 3 (1964), 3–38.CrossRefGoogle Scholar
Balderrama, W., Algebraic theories of power operations, Preprint (2021), arXiv:2108.06802v2.Google Scholar
Barthel, T. and Heard, D., The $E_2$-term of the $K(n)$-local $E_n$-Adams spectral sequence, Topology Appl. 206 (2016), 190–214.CrossRefGoogle Scholar
Behrens, M., Notes on the construction of tmf, in Topological modular forms, eds Douglas, C. L., Francis, J., Henriques, A. G. and Hill, M. A., Mathematical Surveys and Monographs, vol. 201 (American Mathematical Society, Providence, RI, 2014), 131–188.Google Scholar
Berwick-Evans, D., Supersymmetric field theories and the elliptic index theorem with complex coefficients, Geom. Topol. 25 (2021), 2287–2384.CrossRefGoogle Scholar
Bousfield, A. K., The localization of spectra with respect to homology, Topology 18 (1979), 257–281.CrossRefGoogle Scholar
Bousfield, A. K., Uniqueness of infinite deloopings for $K$-theoretic spaces, Pacific J. Math. 129 (1987), 1–31.CrossRefGoogle Scholar
Burklund, R., Schlank, T. M. and Yuan, A., The chromatic Nullstellensatz, Preprint (2022), arXiv:2207.09929v1.Google Scholar
Costello, K., A geometric construction of the Witten genus, I, in Proceedings of the International Congress of Mathematicians. Volume II (Hindustan Book Agency, New Delhi, 2010), 942–959.Google Scholar
Costello, K., A geometric construction of the Witten genus, II, Preprint (2011), arXiv:1112.0816.Google Scholar
Deligne, P. and Rapoport, M., Les schémas de modules de courbes elliptiques, in Modular functions of one variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, vol. 349 (Springer, Berlin, Heidelberg, 1973), 143–316.Google Scholar
Douglas, C. L. and Henriques, A. G., Topological modular forms and conformal nets, in Mathematical foundations of quantum field theory and perturbative string theory, Proceedings of Symposia in Pure Mathematics, vol. 83 (American Mathematical Society, Providence, RI, 2011), 341–354.CrossRefGoogle Scholar
Douglas, L., Francis, J., Henriques, A. G. and Hill, M. A. (eds), Topological modular forms, Mathematical Surveys and Monographs, vol. 201 (American Mathematical Society, Providence, RI, 2014).Google Scholar
Gille, P. and Szamuely, T., Central simple algebras and Galois cohomology, Cambridge Studies in Advanced Mathematics, vol. 101 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Goerss, P. G. and Hopkins, M. J., Moduli spaces of commutative ring spectra, in Structured ring spectra, London Mathematical Society Lecture Note Series, vol. 315 (Cambridge University Press, Cambridge, 2004), 151–200.CrossRefGoogle Scholar
Hill, M. and Lawson, T., Topological modular forms with level structure, Invent. Math. 203 (2016), 359–416.CrossRefGoogle Scholar
Hirzebruch, F., Elliptic genera of level N for complex manifolds, in Differential geometrical methods in theoretical physics (Como, 1987), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 250 (Kluwer Academic Publishers, Dordrecht, 1988), 37–63.CrossRefGoogle Scholar
Hopkins, M. J., Kuhn, N. J. and Ravenel, D. C., Generalized group characters and complex oriented cohomology theories, J. Amer. Math. Soc. 13 (2000), 553–594.CrossRefGoogle Scholar
Hopkins, M. J. and Lawson, T., Strictly commutative complex orientation theory, Math. Z. 290 (2018), 83–101.CrossRefGoogle Scholar
Hovey, M. and Sadofsky, H., Invertible spectra in the $E(n)$-local stable homotopy category, J. Lond. Math. Soc. (2) 60 (1999), 284–302.CrossRefGoogle Scholar
Hovey, M. and Strickland, N. P., Morava $K$-theories and localisation, Mem. Amer. Math. Soc. 139 (1999).Google Scholar
Joachim, M., Higher coherences for equivariant K-theory, in Structured ring spectra, London Mathematical Society Lecture Note Series, vol. 315 (Cambridge University Press, Cambridge, 2004), 87–114.CrossRefGoogle Scholar
Katz, N., Serre-Tate local moduli, in Algebraic surfaces (Orsay, 1976–78), Lecture Notes in Mathematics, vol. 868 (Springer, Berlin-New York, 1981), 138–202.Google Scholar
Kuhn, N. J., Morava K-theories and infinite loop spaces, in Algebraic topology (Arcata, CA, 1986), Lecture Notes in Mathematics, vol. 1370 (Springer, Berlin, 1989), 243–257.CrossRefGoogle Scholar
Lawson, T., Secondary power operations and the Brown-Peterson spectrum at the prime 2, Ann. of Math. (2) 188 (2018), 513–576.CrossRefGoogle Scholar
Lurie, J., Elliptic cohomology I, Preprint (2018), available online at http://www.math.ias.edu/~lurie/.Google Scholar
Lurie, J., Elliptic cohomology II: orientations, Preprint (2018), available online at http://www.math.ias.edu/~lurie/.Google Scholar
Meier, L., Connective models for topological modular forms of level $n$, Preprint (2021), arXiv:2104.12649v1.Google Scholar
Meier, L., Additive decompositions for rings of modular forms, Doc. Math. 27 (2022), 427–488.CrossRefGoogle Scholar
Meier, L., Topological modular forms with level structure: decompositions and duality, Trans. Amer. Math. Soc. 375 (2022), 1305–1355.Google Scholar
Oliver, B., $p$-stubborn subgroups of classical compact Lie groups, J. Pure Appl. Algebra 92 (1994), 55–78.CrossRefGoogle Scholar
Quillen, D., Elementary proofs of some results of cobordism theory using Steenrod operations, Adv. Math. 7 (1971), 29–56.CrossRefGoogle Scholar
Ravenel, D. C., Localization with respect to certain periodic homology theories, Amer. J. Math. 106 (1984), 351–414.CrossRefGoogle Scholar
Ravenel, D. C., Complex cobordism and stable homotopy groups of spheres, Pure and Applied Mathematics, vol. 121 (Academic Press, Orlando, FL, 1986).Google Scholar
Ravenel, D. C., Wilson, W. S. and Yagita, N., Brown-Peterson cohomology from Morava $K$-theory, K-Theory 15 (1998), 147–199.CrossRefGoogle Scholar
Rezk, C., Power operations in Morava $E$-theory: structure and calculations (draft), Preprint (2013), available online at https://faculty.math.illinois.edu/~rezk/power-ops-ht-2.pdf.Google Scholar
Schuster, B. and Yagita, N., Morava $K$-theory of extraspecial 2-groups, Proc. Amer. Math. Soc. 132 (2004), 1229–1239.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks project (2023), https://stacks.math.columbia.edu.Google Scholar
Stolz, S. and Teichner, P., What is an elliptic object?, in Topology, geometry and quantum field theory, London Mathematical Society Lecture Note Series, vol. 308 (Cambridge University Press, Cambridge, 2004), 247–343.CrossRefGoogle Scholar
Stolz, S. and Teichner, P., Supersymmetric field theories and generalized cohomology, in Mathematical foundations of quantum field theory and perturbative string theory, Proceedings of Symposia in Pure Mathematics, vol. 83 (American Mathematical Society, Providence, RI, 2011), 279–340.CrossRefGoogle Scholar
Strickland, N. P., Formal schemes and formal groups, in Homotopy invariant algebraic structures (Baltimore, MD, 1998), Contemporary Mathematics, vol. 239 (American Mathematical Society, Providence, RI, 1999), 263–352.CrossRefGoogle Scholar
Tezuka, M. and Yagita, N., Cohomology of finite groups and Brown-Peterson cohomology, in Algebraic topology (Arcata, CA, 1986), Lecture Notes in Mathematics, vol. 1370 (Springer, Berlin, 1989), 396–408.CrossRefGoogle Scholar
Wilson, D., Orientations and topological modular forms with level structure, Preprint (2015), arXiv:1507.05116v1.Google Scholar
Witten, E., Elliptic genera and quantum field theory, Comm. Math. Phys. 109 (1987), 525–536.CrossRefGoogle Scholar
Witten, E., The index of the Dirac operator in loop space, in Elliptic curves and modular forms in algebraic topology (Princeton, NJ, 1986), Lecture Notes in Mathematics, vol. 1326 (Springer, Berlin, 1988), 161–181.CrossRefGoogle Scholar
Yagita, N., Integral and BP cohomologies of extraspecial $p$-groups for odd primes, Kodai Math. J. 28 (2005), 1–30.CrossRefGoogle Scholar
Zhu, Y., Norm coherence for descent of level structures on formal deformations, J. Pure Appl. Algebra 224 (2020), 106382.CrossRefGoogle Scholar