Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wood, Melanie Matchett
2018.
Cohen-Lenstra heuristics and local conditions.
Research in Number Theory,
Vol. 4,
Issue. 4,
Wood, Melanie Matchett
2019.
Nonabelian Cohen–Lenstra moments.
Duke Mathematical Journal,
Vol. 168,
Issue. 3,
Jordan, Bruce
Klagsbrun, Zev
Poonen, Bjorn
Skinner, Christopher
and
Zaytman, Yevgeny
2020.
Statistics of K-groups modulo p for the ring of
integers of a varying quadratic number field.
Tunisian Journal of Mathematics,
Vol. 2,
Issue. 2,
p.
287.
König, Joachim
Neftin, Danny
and
Sonn, Jack
2020.
Unramified extensions over low degree number fields.
Journal of Number Theory,
Vol. 212,
Issue. ,
p.
72.
Liu, Yuan
and
Wood, Melanie Matchett
2020.
The free group onngenerators modulon+urandom relations asngoes to infinity.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2020,
Issue. 762,
p.
123.
Klys, Jack
2020.
The distribution of p-torsion in degree p cyclic
fields.
Algebra & Number Theory,
Vol. 14,
Issue. 4,
p.
815.
Wood, Melanie Matchett
2021.
An algebraic lifting invariant of Ellenberg, Venkatesh, and Westerland.
Research in the Mathematical Sciences,
Vol. 8,
Issue. 2,
Boston, Nigel
Bush, Michael R.
and
Hajir, Farshid
2021.
HEURISTICS FOR -CLASS TOWERS OF REAL QUADRATIC FIELDS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 20,
Issue. 4,
p.
1429.
Koymans, Peter
and
Pagano, Carlo
2022.
Higher genus theory.
International Mathematics Research Notices,
Vol. 2022,
Issue. 4,
p.
2772.
Liu, Yuan
Wood, Melanie Matchett
and
Zureick-Brown, David
2024.
Publisher Correction to: A predicted distribution for Galois groups of maximal unramified extensions.
Inventiones mathematicae,
Vol. 237,
Issue. 1,
p.
117.
Sawin, Will
and
Wood, Melanie Matchett
2024.
Publisher Correction to: Finite quotients of 3-manifold groups.
Inventiones mathematicae,
Vol. 237,
Issue. 1,
p.
441.
Liu, Yuan
Wood, Melanie Matchett
and
Zureick-Brown, David
2024.
A predicted distribution for Galois groups of maximal unramified extensions.
Inventiones mathematicae,
Vol. 237,
Issue. 1,
p.
49.
Sawin, Will
and
Wood, Melanie Matchett
2024.
Finite quotients of 3-manifold groups.
Inventiones mathematicae,
Vol. 237,
Issue. 1,
p.
349.
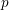 $p$ extensions of imaginary quadratic number fields for
$p$ extensions of imaginary quadratic number fields for 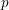 $p$ an odd prime. In this paper, we find the moments of their proposed distribution, and further prove there is a unique distribution with those moments. Further, we show that in the function field analog, for imaginary quadratic extensions of
$p$ an odd prime. In this paper, we find the moments of their proposed distribution, and further prove there is a unique distribution with those moments. Further, we show that in the function field analog, for imaginary quadratic extensions of 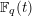 $\mathbb{F}_{q}(t)$, the Galois groups of the maximal unramified pro-
$\mathbb{F}_{q}(t)$, the Galois groups of the maximal unramified pro-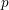 $p$ extensions, as
$p$ extensions, as 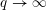 $q\rightarrow \infty$, have the moments predicted by the Boston, Bush and Hajir heuristics. In fact, we determine the moments of the Galois groups of the maximal unramified pro-odd extensions of imaginary quadratic function fields, leading to a conjecture on Galois groups of the maximal unramified pro-odd extensions of imaginary quadratic number fields.
$q\rightarrow \infty$, have the moments predicted by the Boston, Bush and Hajir heuristics. In fact, we determine the moments of the Galois groups of the maximal unramified pro-odd extensions of imaginary quadratic function fields, leading to a conjecture on Galois groups of the maximal unramified pro-odd extensions of imaginary quadratic number fields.

