Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T05:04:17.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Newton non-degenerate $\mu$-constant deformations admit simultaneous embedded resolutions

Part of: Singularities Local theory Birational geometry

Published online by Cambridge University Press:  11 August 2022

Maximiliano Leyton-Álvarez ,
Hussein Mourtada  and
Mark Spivakovsky
Maximiliano Leyton-Álvarez
Affiliation:
Instituto de Matemáticas, Universidad de Talca, Camino Lircay S\N, Campus Norte, 3460787, Talca, Chile [email protected] [email protected]
Hussein Mourtada
Affiliation:
Université Paris Cité and Sorbonne Université, CNRS, IMJ-PRG, F-75013 Paris, France [email protected]
Mark Spivakovsky
Affiliation:
Institut de Mathématiques de Toulouse, UMR 5219 du CNRS, Université Paul Sabatier, CNRS, 118 route de Narbonne, 31062 Toulouse, France [email protected] LaSol, UMI 2001, Instituto de Matemáticas, Unidad de Cuernavaca, Av. Universidad s/n Periferica, Cuernavaca, 62210 Morelos, Mexico
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 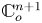$ {\mathbb {C}}^{n+1}_o$ denote the germ of 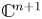$ {\mathbb {C}}^{n+1}$ at the origin. Let 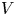$V$ be a hypersurface germ in 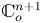$ {\mathbb {C}}^{n+1}_o$ and 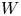$W$ a deformation of 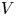$V$ over 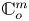$ {\mathbb {C}}_{o}^{m}$. Under the hypothesis that 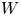$W$ is a Newton non-degenerate deformation, in this article we prove that 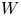$W$ is a 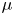$\mu$-constant deformation if and only if 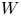$W$ admits a simultaneous embedded resolution. This result gives a lot of information about 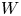$W$, for example, the topological triviality of the family 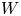$W$ and the fact that the natural morphism 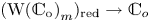$(\operatorname {W( {\mathbb {C}}_{o})}_{m})_{{\rm red}}\rightarrow {\mathbb {C}}_{o}$ is flat, where 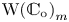$\operatorname {W( {\mathbb {C}}_{o})}_{m}$ is the relative space of 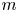$m$-jets. On the way to the proof of our main result, we give a complete answer to a question of Arnold on the monotonicity of Newton numbers in the case of convenient Newton polyhedra.

Keywords

algebraic geometrysingularities of algebraic varietiesdeformations of singularitiessimultaneous embedded resolutionsMilnor numberNewton numberm-jet spaces

MSC classification

Primary: 14B05: Singularities 14B07: Deformations of singularities 14B25: Local structure of morphisms 14E15: Global theory and resolution of singularities 14E25: Embeddings 32S15: Equisingularity (topological and analytic)
Secondary: 32S05: Local singularities 32S10: Invariants of analytic local rings
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 6 , June 2022 , pp. 1268 - 1297
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is partially supported by Projects ANID FONDECYT 1170743 and 1221535. The second author is partially supported by Projet ANR LISA, ANR-17-CE40-0023.

References

Arnold, V. I., Arnold's problems (Springer, Berlin–Heidelberg–New York & PHASIS, 2005).CrossRefGoogle Scholar
Abderrahmane, O. M., On deformation with constant Milnor number and Newton polyhedron, Math. Z. 284 (2016), 167–174.CrossRefGoogle Scholar
Altmann, K., Equisingular deformations of isolated $2$-dimensional hypersurface singularities, Invent. Math. 88 (1987), 619–634.CrossRefGoogle Scholar
Bivia-Ausina, C., Mixed Newton numbers and isolated complete intersection singularities, Proc. Lond. Math. Soc. 94 (2007), 749–771.CrossRefGoogle Scholar
Briançon, J. and Speder, J. P., La trivialité topologique n'implique pas les conditions de Whitney, C. R. Acad. Sci. Paris Sér. I Math. A-B280 (1975), 365–367.Google Scholar
Brzostowski, S., Krasiński, T. and Walewska, J., Arnold's problem on monotonicity of the Newton number for surface singularities, J. Math. Soc. Japan 71 (2019), 1257–1268.CrossRefGoogle Scholar
Furuya, M., Lower bound of Newton number, Tokyo J. Math. 27 (2004), 177–186.CrossRefGoogle Scholar
Greuel, G.-M., Constant Milnor number implies constant multiplicity for quasihomogeneous singularities, Manuscripta Math. 56 (1986), 159–166.CrossRefGoogle Scholar
Ishii, S., A resolution of singularities of toric variety and non-degenerate hypersurface, in Singularities in geometry and topology (World Scientific, Hackensack, NJ, 2007), 354–369.CrossRefGoogle Scholar
Kouchnirenko, A. G., Polyèdres de Newton et nombres de Milnor, Invent. Math. 32 (1976), 1–31.CrossRefGoogle Scholar
Leyton-Álvarez, M., Deforming spaces of $m$-jets of hypersurfaces singularities, J. Algebra 508 (2018), 81–97.CrossRefGoogle Scholar
Lê Dũng, T. and Ramanujam, C. P., The invariance of Milnor's number implies the invariance of the topological type, Amer. J. Math. 98 (1976), 67–78.Google Scholar
Lê Dũng, T. and Saito, K., La constance du nombre de Milnor donne des bonnes stratifications, C. R. Acad. Sci. Paris Sér. A-B 277 (1973), A793–A795.Google Scholar
Mather, J., Notes on topological stability, Bull. Amer. Math. Soc. (N.S.) 49 (2012), 475–506.CrossRefGoogle Scholar
Milnor, J., Singular points of complex hypersurfaces, Annals of Mathematics Studies, no. 61 (Princeton University Press/University of Tokyo Press, Princeton, NJ/Tokyo, 1968).Google Scholar
Mourtada, H., Jet schemes and generating sequences of divisorial valuations in dimension two, Michigan Math. J. 66 (2017), 155–174.CrossRefGoogle Scholar
Nguyen, T. T., Uniform stable radius and Milnor number for non-degenerate isolated complete intersection singularities, Preprint (2020), arXiv:1912.10655.Google Scholar
Oka, M., On the resolution of the hypersurface singularities, in Complex analytic singularities, Advanced Studies in Pure Mathematics, vol. 8 (North-Holland, Amsterdam, 1987), 405–436.CrossRefGoogle Scholar
Oka, M., On the weak simultaneous resolution of a negligible truncation of the Newton boundary, in Singularities (Iowa City, IA, 1986), Contemporary Mathematics, vol. 90 (American Mathematical Society, Providence, RI, 1989), 199–210.Google Scholar
Parusinski, A., Topological triviality of $\mu$-constant deformations of type $f(x)+tg(x)$, Bull. Lond. Math. Soc. 31 (1999), 686–692.CrossRefGoogle Scholar
Teissier, B., Cycles évanescents, sections planes et conditions de Whitney, in Singularités à Cargèse (Rencontre Singularités Géom. Anal., Inst. Études Sci., Cargèse, 1972), Astérisque, nos. 7 et 8 (Société Mathématique de France, Paris, 1973), 285–362.Google Scholar
Teissier, B., Overweight deformations of affine toric varieties and local uniformization, in Valuation theory in interaction, EMS Series Congress Reports (European Mathematical Society, Zürich, 2014), 474–565.CrossRefGoogle Scholar
Tevelev, J., On a question of B. Teissier, Collect. Math. 65 (2014), 61–66.CrossRefGoogle Scholar
Varchenko, A. N., Zeta-function of monodromy and Newton's diagram, Invent. Math. 37 (1976), 253–262.CrossRefGoogle Scholar
Vojta, P., Jets via Hasse-Schmidt derivations, in Diophantine geometry, CRM Series, vol. 4 (Ed. Norm., Pisa, 2007), 335–361.Google Scholar