Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T04:58:36.353Z Has data issue: false hasContentIssue false
  • English
  • Français

Motivic and real étale stable homotopy theory

Part of: (Co)homology theory

Published online by Cambridge University Press:  20 March 2018

Tom Bachmann
Tom Bachmann*
Affiliation:
Fakultät Mathematik, Universität Duisburg-Essen, Thea-Leymann-Straße 9, 45127 Essen, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

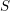Let $S$ be a Noetherian scheme of finite dimension and denote by 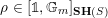$\unicode[STIX]{x1D70C}\in [\unicode[STIX]{x1D7D9},\mathbb{G}_{m}]_{\mathbf{SH}(S)}$ the (additive inverse of the) morphism corresponding to 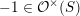$-1\in {\mathcal{O}}^{\times }(S)$ . Here 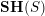$\mathbf{SH}(S)$ denotes the motivic stable homotopy category. We show that the category obtained by inverting 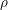$\unicode[STIX]{x1D70C}$ in 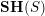$\mathbf{SH}(S)$ is canonically equivalent to the (simplicial) local stable homotopy category of the site 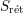$S_{\text{r}\acute{\text{e}}\text{t}}$ , by which we mean the small real étale site of 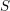$S$ , comprised of étale schemes over 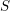$S$ with the real étale topology. One immediate application is that 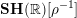$\mathbf{SH}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]$ is equivalent to the classical stable homotopy category. In particular this computes all the stable homotopy sheaves of the 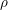$\unicode[STIX]{x1D70C}$ -local sphere (over 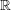$\mathbb{R}$ ). As further applications we show that 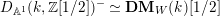$D_{\mathbb{A}^{1}}(k,\mathbb{Z}[1/2])^{-}\simeq \mathbf{DM}_{W}(k)[1/2]$ (improving a result of Ananyevskiy–Levine–Panin), reprove Röndigs’ result that 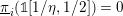$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])=0$ for 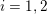$i=1,2$ and establish some new rigidity results.

Keywords

motivic homotopy theorysemi-algebraic topology

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 5 , May 2018 , pp. 883 - 917
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ananyevskiy, A., Levine, M. and Panin, I., Witt sheaves and the 𝜂-inverted sphere spectrum , J. Topol. 10 (2017), 370–385.CrossRefGoogle Scholar
Andradas, C., Bröcker, L. and Ruiz, J. M., Constructible sets in real geometry, vol. 33 (Springer, 2012).Google Scholar
Ayoub, J., Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique, vol. 315 (Société mathématique de France, 2007).Google Scholar
Bachmann, T., On the conservativity of the functor assigning to a motivic spectrum its motive, Duke Math. J., to appear. Preprint (2016), arXiv:1506.07375.Google Scholar
Balmer, P., Spectra, spectra, spectra–tensor triangular spectra versus Zariski spectra of endomorphism rings , Algebr. Geom. Topol. 10 (2010), 1521–1563.CrossRefGoogle Scholar
Barwick, C., On left and right model categories and left and right Bousfield localizations , Homology, Homotopy Appl. 12 (2010), 245–320.Google Scholar
Calmès, B. and Fasel, J., Finite Chow–Witt correspondences, Preprint (2017),arXiv:1412.2989v2.Google Scholar
Cisinski, D.-C. and Déglise, F., Local and stable homological algebra in Grothendieck abelian categories , Homology, Homotopy Appl. 11 (2009), 219–260.CrossRefGoogle Scholar
Cisinski, D.-C. and Déglise, F., Triangulated categories of mixed motives, Preprint (2012),arXiv:0912.2110v3.Google Scholar
Cisinski, D.-C. and Déglise, F., Étale motives , Compos. Math. 152 (2013), 556–666.Google Scholar
Delfs, H., Homology of locally semialgebraic spaces, Lecture Notes in Mathematics, vol. 1484 (Springer, 1991).Google Scholar
Dugger, D., Coherence for invertible objects and multigraded homotopy rings , Algebr. Geom. Topol. 14 (2014), 1055–1106.CrossRefGoogle Scholar
Gabber, O., K-theory of Henselian local rings and Henselian pairs , Contemp. Math. 126 (1992), 59–70.CrossRefGoogle Scholar
Gabber, O. and Kelly, S., Points in algebraic geometry , J. Pure Appl. Algebra 219 (2015), 4667–4680.Google Scholar
Gille, S., On quadratic forms over semilocal rings , Trans. Amer. Math. Soc. (2017), to appear.Google Scholar
Gille, S., Scully, S. and Zhong, C., Milnor–Witt K-groups of local rings , Adv. Math. 286 (2016), 729–753.Google Scholar
Gillet, H. A. and Thomason, R. W., The K-theory of strict Hensel local rings and a theorem of Suslin , J. Pure Appl. Algebra 34 (1984), 241–254.Google Scholar
Heller, J. and Ormsby, K., Galois equivariance and stable motivic homotopy theory , Trans. Amer. Math. Soc. 368 (2016), 8047–8077.CrossRefGoogle Scholar
Hirschhorn, P. S., Model categories and their localizations, vol. 99 (American Mathematical Society, 2009).Google Scholar
Hovey, M., Spectra and symmetric spectra in general model categories , J. Pure Appl. Algebra 165 (2001), 63–127.CrossRefGoogle Scholar
Hornbostel, J. and Yagunov, S., Rigidity for Henselian local rings and A1 -representable theories , Math. Z. 255 (2007), 437–449.Google Scholar
Hoyois, M., Cdh descent in equivariant homotopy K-theory, Preprint (2017),arXiv:1604.06410v3.Google Scholar
Hu, P., Kriz, I. and Ormsby, K., Convergence of the motivic Adams spectral sequence , J. K-Theory 7 (2011), 573–596.CrossRefGoogle Scholar
Jacobson, J., Real cohomology and the powers of the fundamental ideal in the Witt ring , Ann. K-Theory 2 (2017), 357–385.Google Scholar
Jardine, J. F., Local homotopy theory (Springer, 2015).Google Scholar
Karoubi, M., Schlichting, M. and Weibel, C., The Witt group of real algebraic varieties , J. Topol. 9 (2016), 1257–1302.Google Scholar
Knebusch, M., Symmetric bilinear forms over algebraic varieties, conference on quadratic forms , in Queen’s papers in pure and applied mathematics, vol. 46, ed. Orzech, G. (Queens University, Kingston, ON, 1977), 103–283.Google Scholar
Lurie, J., Higher topos theory, vol. 170 (Princeton University Press, 2009).Google Scholar
Lurie, J., Higher algebra (2016), available athttp://www.math.harvard.edu/∼lurie/papers/HA.pdf.Google Scholar
May, J. P. and Sigurdsson, J., Parametrized homotopy theory, vol. 132 (American Mathematical Society, Providence, RI, 2006).CrossRefGoogle Scholar
Milnor, J. W. and Husemoller, D., Symmetric bilinear forms, vol. 60 (Springer, 1973).Google Scholar
Morel, F., An introduction to A1 -homotopy theory , ICTP Trieste Lecture Note Ser. 15 (2003), 357–441.Google Scholar
Morel, F., Sur les puissances de l’idéal fondamental de l’anneau de Witt , Comment. Math. Helv. 79 (2004), 689–703.CrossRefGoogle Scholar
Morel, F., The stable A1 -connectivity theorems , K-Theory 35 (2005), 1–68.CrossRefGoogle Scholar
Morel, F., A1 -algebraic topology over a field, Lecture Notes in Mathematics (Springer, Berlin, Heidelberg, 2012).Google Scholar
Morel, F. and Voevodsky, V., A1 -homotopy theory of schemes , Publ. Math. Inst. Hautes Études Sci. 90 (1999), 45–143 (English).Google Scholar
Röndigs, O., On the 𝜂-inverted sphere , TIFR Proc. Int. Colloq. K-theory (2016), to appear.Google Scholar
Röndigs, O. and Østvær, P., Rigidity in motivic homotopy theory , Math. Ann. 341 (2008), 651–675 (English).Google Scholar
Röndigs, O., Spitzweck, M. and Østvær, P. A., The first stable homotopy groups of motivic spheres, Preprint (2016), arXiv:1604.00365.Google Scholar
Scharlau, W., Quadratic and Hermitian forms, Grundlehren der mathematischen Wissenschaften, vol. 270 (Springer, 1985).CrossRefGoogle Scholar
Scheiderer, C., Real and etale cohomology, Lecture Notes in Mathematics, vol. 1588 (Springer, Berlin, 1994).Google Scholar
Suslin, A., On the K-theory of algebraically closed fields , Invent. Math. 73 (1983), 241–245.CrossRefGoogle Scholar
Suslin, A. and Voevodsky, V., Singular homology of abstract algebraic varieties , Invent. Math. 123 (1996), 61–94.Google Scholar
The Stacks Project Authors, Stacks Project, http://stacks.math.columbia.edu, 2017.Google Scholar