Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T14:38:27.148Z Has data issue: false hasContentIssue false
  • English
  • Français

Morphisms between Cremona groups, and characterization of rational varieties

Part of: Algebraic groups Automorphic functions Birational geometry Complex spaces with a group of automorphisms

Published online by Cambridge University Press:  25 June 2014

Serge Cantat
Serge Cantat*
Affiliation:
Institut de Recherches Mathématiques de Rennes (IRMAR), UMR 6625 (CNRS), Université de Rennes 1, Rennes, France email [email protected] Current address: Département de Mathématiques et Applications (DMA), UMR 8553 (CNRS), ENS Ulm, Paris, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We classify all (abstract) homomorphisms from the group 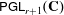$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\sf PGL}_{r+1}(\mathbf{C})$ to the group 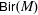${\sf Bir}(M)$ of birational transformations of a complex projective variety 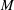$M$, provided that 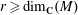$r\geq \dim _\mathbf{C}(M)$. As a byproduct, we show that: (i) 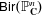${\sf Bir}(\mathbb{P}^n_\mathbf{C})$ is isomorphic, as an abstract group, to 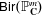${\sf Bir}(\mathbb{P}^m_\mathbf{C})$ if and only if 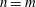$n=m$; and (ii) 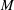$M$ is rational if and only if 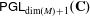${\sf PGL}_{\dim (M)+1}(\mathbf{C})$ embeds as a subgroup of 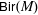${\sf Bir}(M)$.

Keywords

Cremona groupsrational varietiesalgebraic transformation groups

MSC classification

Secondary: 14E07: Birational automorphisms, Cremona group and generalizations 14E08: Rationality questions 14L30: Group actions on varieties or schemes (quotients) 32M05: Complex Lie groups, automorphism groups acting on complex spaces
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 7 , July 2014 , pp. 1107 - 1124
Copyright
© The Author 2014 

References

Barlet, D., Espace analytique réduit des cycles analytiques complexes compacts d’un espace analytique complexe de dimension finie, in Fonctions de plusieurs variables complexes, II (Sém. François Norguet, 1974–1975), Lecture Notes in Mathematics, vol. 482 (Springer, Berlin, 1975), 1–158.Google Scholar
Beauville, A., p-elementary subgroups of the Cremona group, J. Algebra 314 (2) (2007), 553–564.Google Scholar
Blanc, J. and Déserti, J., Degree growth of birational maps of the plane, Ann. Sc. Norm. Super. Pisa Cl. Sci. (2011), 1–17, to appear, arXiv:1109.6810.Google Scholar
Blanc, J. and Furter, J.-P., Topologies and structures on the Cremona group, Ann. of Math. (2) 178 (2012), 1173–1198.Google Scholar
Borel, A. and Tits, J., Homomorphismes ‘abstraits’ de groupes algébriques simples, Ann. of Math. (2) 97 (1973), 499–571.Google Scholar
Campana, F. and Peternell, Th., Cycle spaces, in Several complex variables, VII, Encyclopaedia Mathematical Sciences, vol. 74 (Springer, Berlin, 1994), 319–349.CrossRefGoogle Scholar
Cantat, S., Chambert-Loir, A. and Guedj, V., Quelques aspects des systèmes dynamiques polynomiaux, Panoramas et Synthèses, vol. 30 (Société Mathématique de France, Paris, 2010).Google Scholar
Cantat, S. and Zeghib, A., Holomorphic actions, Kummer examples, and Zimmer program, Ann. Sci. Éc. Norm. Supér. 45 (2012), 447–489.Google Scholar
Cartan, E., Sur les représentations linéaires des groupes clos, Comment. Math. Helv. 2 (1930), 269–283.Google Scholar
Cerveau, D. and Déserti, J., Transformations birationnelles de petit degré, Cours Spécialisés, vol. 19 (Société Mathématique de France, Paris, 2013).Google Scholar
Clemens, C. H. and Griffiths, P. A., The intermediate Jacobian of the cubic threefold, Ann. of Math. (2) 95 (1972), 281–356.Google Scholar
Demazure, M., Sous-groupes algébriques de rang maximum du groupe de Cremona, Ann. Sci. Éc. Norm. Supér. (4) 3 (1970), 507–588.Google Scholar
Déserti, J., Sur les automorphismes du groupe de Cremona, Compositio Math. 142 (2006), 1459–1478.Google Scholar
Déserti, J., Sur les sous-groupes nilpotents du groupe de Cremona, Bull. Braz. Math. Soc. (N.S.) 38 (2007), 377–388.Google Scholar
Dieudonné, J. A., La géométrie des groupes classiques, 3rd edition, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 5 (Springer, Berlin, 1971).Google Scholar
Dinh, T.-C. and Sibony, N., Une borne supérieure pour l’entropie topologique d’une application rationnelle, Ann. of Math. (2) 161 (2005), 1637–1644.Google Scholar
Epstein, D. B. A. and Thurston, W. P., Transformation groups and natural bundles, Proc. Lond. Math. Soc. (3) 38 (1979), 219–236.Google Scholar
Filipkiewicz, R. P., Isomorphisms between diffeomorphism groups, Ergodic Theory Dynam. Systems 2 (1982), 159–171.Google Scholar
Ghys, É., Prolongements des difféomorphismes de la sphère, Enseign. Math. (2) 37 (1991), 45–59.Google Scholar
Ghys, É., Sur les groupes engendrés par des difféomorphismes proches de l’identité, Bol. Soc. Brasil. Mat. (N.S.) 24 (1993), 137–178.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III, Publ. Math. Inst. Hautes Études Sci. (1966), 255.Google Scholar
Guedj, V., Propriétés ergodiques des applications rationnelles, Panorama et Synthèses, vol. 30 (Société Mathématique de France, Paris, 2010), 97–102.Google Scholar
Hanamura, M., On the birational automorphism groups of algebraic varieties, Compositio Math. 63 (1987), 123–142.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).Google Scholar
Huckleberry, A. and Zaitsev, D., Actions of groups of birationally extendible automorphisms, in Geometric complex analysis (Hayama, 1995) (World Scientific, River Edge, NJ, 1996), 261–285.Google Scholar
Hurtado, S., Continuity of discrete homomorphisms of diffeomorphism groups, Preprint (2013), arXiv:1307.4447.Google Scholar
Kollár, J., Smith, K. E. and Corti, A., Rational and nearly rational varieties, Cambridge Studies in Advanced Mathematics, vol. 92 (Cambridge University Press, Cambridge, 2004).Google Scholar
Lieberman, D. I., Compactness of the Chow scheme: applications to automorphisms and deformations of Kähler manifolds, in Fonctions de plusieurs variables complexes, III (Sém. François Norguet, 1975–1977), Lecture Notes in Mathematics, vol. 670 (Springer, Berlin, 1978), 140–186.Google Scholar
Mann, K., Homomorphisms between diffeomorphism groups, Preprint (2012), arXiv:1206.1196.Google Scholar
Militon, E., Éléments de distorsion de Diff0∞(M), Bull. Soc. Math. France 141 (2013), 35–46.Google Scholar
Prokhorov, Y., p-elementary subgroups of the Cremona group of rank 3, in Classification of algebraic varieties, EMS Series of Congress Reports (Eur. Math. Soc., Zürich, 2011), 327–338.Google Scholar
Umemura, H., Sur les sous-groupes algébriques primitifs du groupe de Cremona à trois variables, Nagoya Math. J. 79 (1980), 47–67.Google Scholar
Umemura, H., Maximal algebraic subgroups of the Cremona group of three variables. Imprimitive algebraic subgroups of exceptional type, Nagoya Math. J. 87 (1982), 59–78.Google Scholar
Weil, A., On algebraic groups of transformations, Amer. J. Math. 77 (1955), 355–391.Google Scholar
Zaitsev, D., Regularization of birational group operations in the sense of Weil, J. Lie Theory 5 (1995), 207–224.Google Scholar