Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Deopurkar, Anand
2013.
Modular compactifications of the space of marked trigonal curves.
Advances in Mathematics,
Vol. 248,
Issue. ,
p.
96.
Smyth, David Ishii
2013.
Towards a classification of modular compactifications of $\mathcal {M}_{g,n}$.
Inventiones mathematicae,
Vol. 192,
Issue. 2,
p.
459.
Hall, Jack
2014.
A relative GAGA principle for families of curves.
Journal of the London Mathematical Society,
Vol. 90,
Issue. 1,
p.
29.
Chen, Dawei
and
Coskun, Izzet
2014.
Extremal effective divisors on $$\overline{\mathcal M}_{1,n}$$ M ¯ 1 , n.
Mathematische Annalen,
Vol. 359,
Issue. 3-4,
p.
891.
Moon, Han-Bom
2015.
A family of divisors on M¯g,n and their log canonical models.
Journal of Pure and Applied Algebra,
Vol. 219,
Issue. 10,
p.
4642.
Pagani, Nicola
2016.
Moduli of abelian covers of elliptic curves.
Journal of Pure and Applied Algebra,
Vol. 220,
Issue. 3,
p.
1258.
Alper, Jarod
Fedorchuk, Maksym
and
Smyth, David Ishii
2016.
Second Flip in the Hassett–Keel Program: Projectivity.
International Mathematics Research Notices,
p.
rnw216.
Polishchuk, Alexander
2017.
Moduli spaces of nonspecial pointed curves of arithmetic genus 1.
Mathematische Annalen,
Vol. 369,
Issue. 3-4,
p.
1021.
Alper, Jarod
Fedorchuk, Maksym
and
Smyth, David Ishii
2017.
Second flip in the Hassett–Keel program: existence of good moduli spaces.
Compositio Mathematica,
Vol. 153,
Issue. 8,
p.
1584.
Polishchuk, Alexander
2017.
Moduli of curves, Gröbner bases, and the Krichever map.
Advances in Mathematics,
Vol. 305,
Issue. ,
p.
682.
Alper, Jarod
Fedorchuk, Maksym
Smyth, David Ishii
and
van der Wyck, Frederick
2017.
Second flip in the Hassett–Keel program: a local description.
Compositio Mathematica,
Vol. 153,
Issue. 8,
p.
1547.
Lekili, Yankı
and
Polishchuk, Alexander
2019.
A modular compactification of ℳ1,n
from A
∞-structures.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 755,
p.
151.
Smyth, David
2019.
Intersections of 𝜓-classes on \overline{𝑀}_{1,𝑛}(𝑚).
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 12,
p.
8679.
Polishchuk, Alexander
2019.
MODULI OF CURVES WITH NONSPECIAL DIVISORS AND RELATIVE MODULI OF -STRUCTURES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 18,
Issue. 06,
p.
1295.
Battistella, Luca
Carocci, Francesca
and
Manolache, Cristina
2020.
Reduced invariants from cuspidal maps.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 9,
p.
6713.
Hamilton, Eloise
2020.
Classifying complete $$\mathbb {C}$$-subalgebras of $$\mathbb {C}[[t]]$$.
manuscripta mathematica,
Vol. 163,
Issue. 3-4,
p.
437.
Bozlee, Sebastian
2021.
Contractions of subcurves of families of log curves.
Communications in Algebra,
Vol. 49,
Issue. 11,
p.
4616.
Battistella, Luca
2022.
Modular compactifications of ℳ2,n with
Gorenstein curves.
Algebra & Number Theory,
Vol. 16,
Issue. 7,
p.
1547.
Battistella, Luca
and
Carocci, Francesca
2023.
A smooth compactification of the space of genus two curves in projective space: via logarithmic geometry and Gorenstein curves.
Geometry & Topology,
Vol. 27,
Issue. 3,
p.
1203.
Bozlee, Sebastian
Kuo, Bob
and
Neff, Adrian
2023.
A classification of modular compactifications of the space of pointed elliptic curves by Gorenstein curves.
Algebra & Number Theory,
Vol. 17,
Issue. 1,
p.
127.


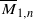 .
.