Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T16:47:36.330Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular compactifications of the space of pointed elliptic curves I

Part of: Curves

Published online by Cambridge University Press:  07 September 2010

David Ishii Smyth
David Ishii Smyth*
Affiliation:
Department of Mathematics, Harvard University, Cambridge, MA 02138, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

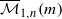We introduce a sequence of isolated curve singularities, the elliptic m-fold points, and an associated sequence of stability conditions, generalizing the usual definition of Deligne–Mumford stability. For every pair of integers 1≤m<n, we prove that the moduli problem of n-pointed m-stable curves of arithmetic genus one is representable by a proper irreducible Deligne–Mumford stack . We also consider weighted variants of these stability conditions, and construct the corresponding moduli stacks 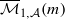. In forthcoming work, we will prove that these stacks have projective coarse moduli and use the resulting spaces to give a complete description of the log minimal model program for .

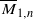Keywords

moduli of curveselliptic curvessingularities

MSC classification

Secondary: 14H10: Families, moduli (algebraic) 14H20: Singularities, local rings
Type
Research Article
Information
Compositio Mathematica , Volume 147 , Issue 3 , May 2011 , pp. 877 - 913
Copyright
Copyright © Foundation Compositio Mathematica 2010

References

[1]Altman, A. and Kleiman, S., Introduction to Grothendieck duality theory, Lecture Notes in Mathematics, vol. 146 (Springer, Berlin, 1970).CrossRefGoogle Scholar
[2]Deligne, P. and Mumford, D., The irreducibility of the space of curves of given genus, Publ. Math. Inst. Hautes Études Sci. 36 (1969), 75–109.CrossRefGoogle Scholar
[3]Hassett, B., Moduli spaces of weighted pointed stable curves, Adv. Math. 173 (2003), 316–352.CrossRefGoogle Scholar
[4]Hassett, B., Classical and minimal models of the moduli space of curves of genus two, in Geometric methods in algebra and number theory, Progress in Mathematics, vol. 235 (Birkhäuser Boston, Boston, MA, 2005), 169–192.CrossRefGoogle Scholar
[5]Hassett, B. and Hyeon, D., Log minimal model program for the moduli space of curves: the first flip, Preprint, arXiv:math.AG/0806.3444.Google Scholar
[6]Hassett, B. and Hyeon, D., Log canonical models for the moduli space of curves: the first divisorial contraction, Trans. Amer. Math. Soc. 361 (2009), 4471–4489.CrossRefGoogle Scholar
[7]Hyeon, D. and Lee, Y., Log minimal model program for the moduli space of stable curves of genus three, Preprint, arXiv:math.AG/0703093.Google Scholar
[8]Kollár, J., Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 32 (Springer, Berlin, 1996).CrossRefGoogle Scholar
[9]Laumon, G. and Moret-Bailly, L., Champs algébriques, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 39 (Springer, Berlin, 2000).CrossRefGoogle Scholar
[10]Lipman, J., Rational singularities, with applications to algebraic surfaces and unique factorization, Publ. Math. Inst. Hautes Études Sci. 36 (1969), 195–279.CrossRefGoogle Scholar
[11]Mumford, D., Fogarty, J. and Kirwan, F., Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)], vol. 34, third edition (Springer, Berlin, 1994).CrossRefGoogle Scholar
[12]Pinkham, H. C., Deformations of algebraic varieties with Gm action, Astérisque, no. 20 (Société Mathématique de France, Paris, 1974).Google Scholar
[13]Schubert, D., A new compactification of the moduli space of curves, Compositio Math. 78 (1991), 297–313.Google Scholar
[14]Sernesi, E., Deformations of algebraic schemes, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 334 (Springer, Berlin, 2006).Google Scholar