Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T02:25:01.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Modified quantum dimensions and re-normalized link invariants

Part of: Groups and algebras in quantum theory Categories with structure Low-dimensional topology

Published online by Cambridge University Press:  01 January 2009

Nathan Geer ,
Bertrand Patureau-Mirand  and
Vladimir Turaev
Nathan Geer
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332-0160, USA (email: [email protected])
Bertrand Patureau-Mirand
Affiliation:
L.M.A.M., Université de Bretagne-Sud, Université Européenne de Bretagne, BP 573, F-56017 Vannes, France (email: [email protected])
Vladimir Turaev
Affiliation:
IRMA, Université Louis Pasteur, CNRS, 7 rue René Descartes, F-67084 Strasbourg, France (email: [email protected]) Department of Mathematics, Indiana University, Rawles Hall, 831 East 3rd Street, Bloomington, IN 47405, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give a re-normalization of the Reshetikhin–Turaev quantum invariants of links, using modified quantum dimensions. In the case of simple Lie algebras these modified quantum dimensions are proportional to the usual quantum dimensions. More interestingly, we give two examples where the usual quantum dimensions vanish but the modified quantum dimensions are non-zero and lead to non-trivial link invariants. The first of these examples is a class of invariants arising from Lie superalgebras previously defined by the first two authors. These link invariants are multivariable and generalize the multivariable Alexander polynomial. 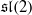The second example is a hierarchy of link invariants arising from nilpotent representations of quantized at a root of unity. These invariants contain Kashaev’s quantum dilogarithm invariants of knots.

Keywords

knotLie algebratensor categoryquantum group

MSC classification

Secondary: 81R50: Quantum groups and related algebraic methods 57M27: Invariants of knots and 3-manifolds 18D10: Monoidal categories (= multiplicative categories), symmetric monoidal categories, braided categories
Type
Research Article
Information
Compositio Mathematica , Volume 145 , Issue 1 , January 2009 , pp. 196 - 212
Copyright
Copyright © Foundation Compositio Mathematica 2009

References

[1]Akutsu, Y., Deguchi, T. and Ohtsuki, T., Invariants of colored links, J. Knot Theory Ramifications 1 (1992), 161–184.CrossRefGoogle Scholar
[2]Geer, N. and Patureau-Mirand, B., On the colored HOMFLY-PT, multivariable and Kashaev link invariants, Commun. Contemp. Math. 10, Suppl. 1 (2008), 993–1011.CrossRefGoogle Scholar
[3]Geer, N. and Patureau-Mirand, B., Multivariable link invariants arising from Lie superalgebras of type I, Pacific J. Math. 238 (2008), 331–348, math.GT/0609034CrossRefGoogle Scholar
[4]Kashaev, R. M., A link invariant from quantum dilogarithm, Modern Phys. Lett. A 10 (1995), 1409–1418.CrossRefGoogle Scholar
[5]Kauffman, L. H. and Saleur, H., Free fermions and the Alexander–Conway polynomial, Comm. Math. Phys. 141 (1991), 293–327.CrossRefGoogle Scholar
[6]Murakami, J., Colored Alexander invariants and cone-manifolds, Osaka J. Math. 45 (2008), 541–564.Google Scholar
[7]Murakami, H. and Murakami, J., The colored Jones polynomials and the simplicial volume of a knot, Acta Math. 186 (2001), 85–104.CrossRefGoogle Scholar
[8]Ohtsuki, T., Quantum invariants, in A study of knots, 3-manifolds, and their sets, Series on Knots and Everything, vol. 29 (World Scientific, River Edge, NJ, 2002).Google Scholar
[9]Turaev, V. G., Quantum invariants of knots and 3-manifolds, de Gruyter Studies in Mathematics, vol. 18 (Walter de Gruyter & Co., Berlin, 1994).CrossRefGoogle Scholar