Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-08T10:32:29.385Z Has data issue: false hasContentIssue false
  • English
  • Français

Mirabolic Satake equivalence and supergroups

Part of: Lie algebras and Lie superalgebras Families, fibrations Special varieties

Published online by Cambridge University Press:  22 July 2021

Alexander Braverman ,
Michael Finkelberg ,
Victor Ginzburg  and
Roman Travkin
Alexander Braverman
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ONM5S 2E4, Canada and Skolkovo Institute of Science and Technology, Moscow, [email protected]
Michael Finkelberg
Affiliation:
Department of Mathematics, National Research University Higher School of Economics, Moscow119048, Russia and Skolkovo Institute of Science and Technology, Moscow, Russia and Institute for the Information Transmission Problems, Moscow, [email protected]
Victor Ginzburg
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL60637, [email protected]
Roman Travkin
Affiliation:
Skolkovo Institute of Science and Technology, Moscow121205, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a mirabolic analogue of the geometric Satake equivalence. We also prove an equivalence that relates representations of a supergroup to the category of 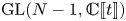$\operatorname{GL}(N-1,{\mathbb {C}}[\![t]\!])$-equivariant perverse sheaves on the affine Grassmannian of 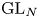$\operatorname{GL}_N$. We explain how our equivalences fit into a more general framework of conjectures due to Gaiotto and to Ben-Zvi, Sakellaridis and Venkatesh.

Keywords

Satake equivalencemirabolic affine Grassmanniansupergroups

MSC classification

Secondary: 14D24: Geometric Langlands program 14M15: Grassmannians, Schubert varieties, flag manifolds 17B20: Simple, semisimple, reductive (super)algebras
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 8 , August 2021 , pp. 1724 - 1765
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

To our friend Sasha Shen on the occasion of his 60th birthday

References

Arkhipov, S. and Gaitsgory, D., Differential operators on the loop group via chiral algebras, Int. Math. Res. Not. IMRN 2002 (2002), 165–210.10.1155/S1073792802102078CrossRefGoogle Scholar
Arkhipov, S. and Gaitsgory, D., Another realization of the category of modules over the small quantum group, Adv. Math. 173 (2003), 114–143.10.1016/S0001-8708(02)00016-6CrossRefGoogle Scholar
Bezrukavnikov, R., On two geometric realizations of an affine Hecke algebra, Publ. Math. Inst. Hautes Études Sci. 123 (2016), 1–67.10.1007/s10240-015-0077-xCrossRefGoogle Scholar
Beilinson, A. and Drinfeld, V., Quantization of Hitchin's integrable system and Hecke eigensheaves, https://math.uchicago.edu/~drinfeld/langlands/QuantizationHitchin.pdf.Google Scholar
Bezrukavnikov, R. and Finkelberg, M., Equivariant Satake category and Kostant–Whittaker reduction, Mosc. Math. J. 8 (2008), 39–72.CrossRefGoogle Scholar
Braden, T., Hyperbolic localization of intersection cohomology, Transform. Groups 8 (2003), 209–216.10.1007/s00031-003-0606-4CrossRefGoogle Scholar
Braverman, A. and Finkelberg, M., A quasi-coherent description of the category $D\operatorname {-mod}({\mathbf {Gr}}_{\operatorname{GL}(n)})$, Preprint (2018), arXiv:1809.10774.Google Scholar
Cogdell, J., Lectures on $L$-functions, converse theorems, and functoriality for $\operatorname{GL}_n$, Fields Inst. Monogr. vol. 20 (American Mathematical Society, Providence, RI, 2004), 1–96.Google Scholar
Drinfeld, V. and Gaitsgory, D., On a theorem of Braden, Transform. Groups 19 (2014), 313–358.10.1007/s00031-014-9267-8CrossRefGoogle Scholar
Finkelberg, M., Ginzburg, V. and Travkin, R., Mirabolic affine Grassmannian and character sheaves, Selecta Math. (N.S.) 14 (2009), 607–628.CrossRefGoogle Scholar
Finkelberg, M. and Ionov, A., Kostka–Shoji polynomials and Lusztig's convolution diagram, Bull. Inst. Math. Acad. Sin. (N.S.) 13 (2018), 31–42.Google Scholar
Gaiotto, D. and Witten, E., $S$-duality of boundary conditions in ${\mathcal {N}}=4$ super Yang–Mills theory, Adv. Theor. Math. Phys. 13 (2009), 721–896.10.4310/ATMP.2009.v13.n3.a5CrossRefGoogle Scholar
Gaitsgory, D., Twisted Whittaker model and factorizable sheaves, Selecta Math. (N.S.) 13 (2008), 617–659.10.1007/s00029-008-0053-0CrossRefGoogle Scholar
Gaitsgory, D., Sheaves of categories and the notion of 1-affineness, in Stacks and Categories in Geometry, Topology, and Algebra, eds T. Pantev et al. , Contemporary Mathematics, vol. 643 (American Mathematical Society, Providence, RI, 2015), 127–225.Google Scholar
Gaitsgory, D., Quantum Langlands correspondence, Preprint (2016), arXiv:1601.05279.Google Scholar
Gaitsgory, D., The local and global versions of the Whittaker category, Pure Appl. Math. Q. 16 (2020), 775–904.10.4310/PAMQ.2020.v16.n3.a14CrossRefGoogle Scholar
Jacquet, H., Piatetski-Shapiro, I. and Shalika, J., Rankin–Selberg convolutions, Amer. J. Math. 105 (1983), 367–464.CrossRefGoogle Scholar
Le Bruyn, L. and Procesi, C., Semisimple representations of quivers, Trans. Amer. Math. Soc. 317 (1990), 585–598.10.1090/S0002-9947-1990-0958897-0CrossRefGoogle Scholar
Lusztig, G., Green polynomials and singularities of unipotent classes, Adv. Math. 42 (1981), 169–178.10.1016/0001-8708(81)90038-4CrossRefGoogle Scholar
Mac Lane, S., Categories for the working mathematician, Graduate Texts in Mathematics, vol. 5, second edition (Springer, New York, 1998).Google Scholar
Mirković, I. and Riche, S., Linear Koszul duality, Compos. Math. 146 (2010), 233–258.CrossRefGoogle Scholar
Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Ann. of Math. (2) 166 (2007), 95–143, Erratum, Ann. of Math. (2) 188 (2018), 1017–1018.CrossRefGoogle Scholar
Mikhaylov, V. and Witten, E., Branes and supergroups, Comm. Math. Phys. 340 (2015), 699–832.CrossRefGoogle Scholar
Sakellaridis, Y., Spherical functions on spherical varieties, Amer. J. Math. 135 (2013), 1291–1381.CrossRefGoogle Scholar
Schieder, S., Monodromy and Vinberg fusion for the principal degeneration of the space of $G$-bundles, Ann. Sci. Éc. Norm. Supér. (4) 52 (2019), 821–866.10.24033/asens.2398CrossRefGoogle Scholar
Shoji, T., Green functions attached to limit symbols, Adv. Stud. Pure Math. 40 (2004), 443–467.CrossRefGoogle Scholar
Travkin, R., Mirabolic Robinson-Shensted-Knuth correspondence, Selecta Math. (N.S.) 14 (2009), 727–758.CrossRefGoogle Scholar
Zhao, Y., Quantum parameters of the geometric Langlands theory, Preprint (2017), arXiv:1708.05108.Google Scholar