Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T04:30:41.416Z Has data issue: false hasContentIssue false
  • English
  • Français

Minor arcs, mean values, and restriction theory for exponential sums over smooth numbers

Part of: Multiplicative number theory Exponential sums and character sums Diophantine equations

Published online by Cambridge University Press:  23 February 2016

Adam J. Harper
Adam J. Harper*
Affiliation:
Jesus College, Cambridge CB5 8BL, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate exponential sums over those numbers 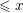${\leqslant}x$ all of whose prime factors are 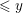${\leqslant}y$. We prove fairly good minor arc estimates, valid whenever 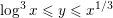$\log ^{3}x\leqslant y\leqslant x^{1/3}$. Then we prove sharp upper bounds for the 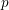$p$th moment of (possibly weighted) sums, for any real 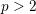$p>2$ and 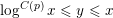$\log ^{C(p)}x\leqslant y\leqslant x$. Our proof develops an argument of Bourgain, showing that this can succeed without strong major arc information, and roughly speaking it would give sharp moment bounds and restriction estimates for any set sufficiently factorable relative to its density. 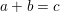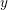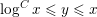By combining our bounds with major arc estimates of Drappeau, we obtain an asymptotic for the number of solutions of $a+b=c$ in $y$-smooth integers less than $x$ whenever $\log ^{C}x\leqslant y\leqslant x$. Previously this was only known assuming the generalised Riemann hypothesis. Combining them with transference machinery of Green, we prove Roth’s theorem for subsets of the 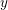$y$-smooth numbers whenever 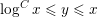$\log ^{C}x\leqslant y\leqslant x$. This provides a deterministic set, of size 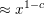${\approx}x^{1-c}$, inside which Roth’s theorem holds.

Keywords

exponential sumscircle methodrestriction theorysmooth numbersxyz conjectureRoth’s theorem

MSC classification

Primary: 11L07: Estimates on exponential sums
Secondary: 11N25: Distribution of integers with specified multiplicative constraints 11D04: Linear equations
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 6 , June 2016 , pp. 1121 - 1158
Copyright
© The Author 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balog, A. and Pomerance, C., The distribution of smooth numbers in arithmetic progressions, Proc. Amer. Math. Soc. 115 (1992), 33–43.CrossRefGoogle Scholar
Balog, A. and Sárkőzy, A., On sums of integers having small prime factors. I, Studia Sci. Math. Hungar. 19 (1984), 35–47.Google Scholar
Bourgain, J., On Λ(p)-subsets of squares, Israel J. Math. 67 (1989), 291–311.CrossRefGoogle Scholar
de la Bretèche, R., Sommes d’exponentielles et entiers sans grand facteur premier, Proc. Lond. Math. Soc. (3) 77 (1998), 39–78.CrossRefGoogle Scholar
de la Bretèche, R., Sommes sans grand facteur premier, Acta Arith. 88 (1999), 1–14.Google Scholar
de la Bretèche, R. and Granville, A., Densité des friables, Bull. Soc. Math. France 142 (2014), 303–348.Google Scholar
de la Bretèche, R. and Tenenbaum, G., Propriétés statistiques des entiers friables, Ramanujan J. 9 (2005), 139–202.Google Scholar
Brüdern, J., A problem in additive number theory, Math. Proc. Cambridge Philos. Soc. 103 (1988), 27–33.Google Scholar
Conlon, D., Fox, J. and Zhao, Y., A relative Szemerédi theorem, Geom. Funct. Anal. 25 (2015), 733–762.Google Scholar
Davenport, H., Multiplicative number theory, third edition (Springer, 2000), revised by H. L. Montgomery.Google Scholar
Drappeau, S., Sur les solutions friables de l’équation a + b = c, Math. Proc. Cambridge Philos. Soc. 154 (2013), 439–463.CrossRefGoogle Scholar
Drappeau, S., Sommes friables d’exponentielles et applications, Canad. J. Math. 67 (2015), 597–638.Google Scholar
Fouvry, E. and Tenenbaum, G., Entiers sans grand facteur premier en progressions arithmetiques, Proc. Lond. Math. Soc. (3) 63 (1991), 449–494.CrossRefGoogle Scholar
Friedlander, J. B., Integers without large prime factors. II, Acta Arith. 39 (1981), 53–57.CrossRefGoogle Scholar
Granville, A., Smooth numbers: computational number theory and beyond, in Algorithmic number theory: lattices, number fields, curves and cryptography, Mathematical Sciences Research Institute Publications, vol. 44 (Cambridge University Press, 2008), 267–323.Google Scholar
Green, B., Roth’s theorem in the primes, Ann. of Math. (2) 161 (2005), 1609–1636.CrossRefGoogle Scholar
Green, B. and Tao, T., Restriction theory of the Selberg sieve, with applications, J. Théor. Nombres Bordeaux 18 (2006), 147–182.CrossRefGoogle Scholar
Ha, J., Some problems in multiplicative number theory, PhD thesis, Stanford University (2014), available at http://searchworks.stanford.edu/view/10408988.Google Scholar
Harper, A. J., Bombieri–Vinogradov and Barban–Davenport–Halberstam type theorems for smooth numbers, Preprint (2012), arXiv:1208.5992.Google Scholar
Helfgott, H. A., Minor arcs for Goldbach’s problem, Preprint (2012), arXiv:1205.5252.Google Scholar
Hildebrand, A., On the number of positive integers ⩽x and free of prime factors >y, J. Number Theory 22 (1986), 289–307.Google Scholar
Hildebrand, A. and Tenenbaum, G., On integers free of large prime factors, Trans. Amer. Math. Soc. 296 (1986), 265–290.CrossRefGoogle Scholar
Hildebrand, A. and Tenenbaum, G., Integers without large prime factors, J. Théor. Nombres Bordeaux 5 (1993), 411–484.Google Scholar
Keil, E., On a diagonal quadric in dense variables, Glasg. Math. J. 56 (2014), 601–628.CrossRefGoogle Scholar
Keil, E., Translation invariant quadratic forms in dense sets, Preprint (2013), arXiv:1308.6680.Google Scholar
Kohayakawa, Y., Łuczak, T. and Rödl, V., Arithmetic progressions of length three in subsets of a random set, Acta Arith. 75 (1996), 133–163.Google Scholar
Kohayakawa, Y., Rödl, V., Schacht, M. and Skokan, J., On the triangle removal lemma for subgraphs of sparse pseudorandom graphs, in An irregular mind, Bolyai Society Mathematical Studies, vol. 21 (János Bolyai Mathematical Society, Budapest, 2010), 359–404.Google Scholar
Lagarias, J. C. and Soundararajan, K., Smooth solutions to the abc equation: the xyz conjecture, J. Théor. Nombres Bordeaux 23 (2011), 209–234.Google Scholar
Lagarias, J. C. and Soundararajan, K., Counting smooth solutions to the equation A+B=C, Proc. Lond. Math. Soc. (3) 104 (2012), 770–798.CrossRefGoogle Scholar
Mirek, M., Roth’s theorem in the Piatetski–Shapiro primes, Rev. Mat. Iberoam. 31 (2015), 617–656.Google Scholar
Montgomery, H. L., Ten lectures on the interface between analytic number theory and harmonic analysis (American Mathematical Society, 1994), Published for the Conference Board of the Mathematical Sciences.Google Scholar
Sárkőzy, G., On sums with small prime factors, Acta Math. Hungar. 67 (1995), 333–345.Google Scholar