Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T05:49:07.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Measures of irrationality for hypersurfaces of large degree

Part of: Surfaces and higher-dimensional varieties Birational geometry Curves Cycles and subschemes

Published online by Cambridge University Press:  04 September 2017

Francesco Bastianelli ,
Pietro De Poi ,
Lawrence Ein ,
Robert Lazarsfeld  and
Brooke Ullery
Francesco Bastianelli
Affiliation:
Dipartimento di Matematica, Università degli Studi di Bari, Via Edoardo Orabona 4, 70125 Bari, Italy email [email protected]
Pietro De Poi
Affiliation:
Dipartimento di Scienze Matematiche, Informatiche e Fisiche, Università degli Studi di Udine, Via delle Scienze 206, 33100 Udine, Italy email [email protected]
Lawrence Ein
Affiliation:
Department of Mathematics, University Illinois at Chicago, 851 South Morgan St., Chicago, IL 60607, USA email [email protected]
Robert Lazarsfeld
Affiliation:
Department of Mathematics, Stony Brook University, Stony Brook, NY 11794, USA email [email protected]
Brooke Ullery
Affiliation:
Department of Mathematics, Harvard University, Cambridge, MA 02138, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

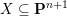We study various measures of irrationality for hypersurfaces of large degree in projective space and other varieties. These include the least degree of a rational covering of projective space, and the minimal gonality of a covering family of curves. The theme is that positivity properties of canonical bundles lead to lower bounds on these invariants. In particular, we prove that if $X\subseteq \mathbf{P}^{n+1}$ is a very general smooth hypersurface of dimension $n$ and degree 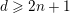$d\geqslant 2n+1$, then any dominant rational mapping 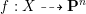$f:X{\dashrightarrow}\mathbf{P}^{n}$ must have degree at least 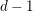$d-1$. We also propose a number of open problems, and we show how our methods lead to simple new proofs of results of Ran and Beheshti–Eisenbud concerning varieties of multi-secant lines.

Keywords

hypersurfacesmeasures of irrationalitypositivitydegree of irrationalitycovering gonality

MSC classification

Primary: 14J70: Hypersurfaces 14E05: Rational and birational maps 14E20: Coverings
Secondary: 14C99: None of the above, but in this section 14H51: Special divisors (gonality, Brill-Noether theory)
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 11 , November 2017 , pp. 2368 - 2393
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramovich, D., A linear lower bound on the gonality of modular curves , Int. Math. Res. Not. IMRN 20 (1996), 1005–1011.Google Scholar
Arrondo, E., Line congruences of low order , Milan J. Math. 70 (2002), 223–243.Google Scholar
Bakker, B. and Tsimerman, J., On the Frey–Mazur conjecture over low genus curves, Preprint (2013), arXiv:1309.6568.Google Scholar
Bastianelli, F., On symmetric products of curves , Trans. Amer. Math. Soc. 364 (2012), 2493–2519.Google Scholar
Bastianelli, F., Ciliberto, C., Flamini, F. and Supino, P., A note on gonality of curves on general hypersurfaces , Boll. Unione Mat. Ital. (9) (2017), doi:10.1007/s40574-017-0129-x, in press.Google Scholar
Bastianelli, F., Cortini, R. and De Poi, P., The gonality theorem of Noether for hypersurfaces , J. Algebraic Geom. 23 (2014), 313–339.Google Scholar
Beheshti, R. and Eisenbud, D., Fibers of generic projections , Compos. Math. 146 (2010), 435–456.Google Scholar
Ein, L., Subvarieties of generic complete intersections , Invent. Math. 94 (1988), 163–169.Google Scholar
Fakhruddin, N., Zero cycles on generic hypersurfaces of large degree, Preprint (2002),arXiv:math/0208179.Google Scholar
Gruson, L. and Peskine, C., On the smooth locus of aligned Hilbert schemes, the k-secant lemma and the general projection theorem , Duke Math. J. 162 (2013), 553–578.CrossRefGoogle Scholar
Guerra, L. and Pirola, G. P., On rational maps from a general surface in P 3 to surfaces of general type , Adv. Geom. 8 (2008), 289–307.Google Scholar
Hartshorne, R. and Schlesinger, E., Gonality of a general ACM curve in P 3 , Pacific J. Math. 251 (2011), 269–313.Google Scholar
Hassett, B., Pirutka, A. and Tschinkel, Y., A very general quartic double fourfold is not stably rational, Preprint (2016), arXiv:1605.03220.Google Scholar
Heinzer, W. and Moh, T. T., On the Lüroth semigroup and Weirstrass canonical divisors , J. Algebra 77 (1982), 62–73.Google Scholar
Hwang, J.-M. and To, W.-K., Injectivity radius and gonality of a compact Riemann surface , Amer. J. Math. (2012), 259–283.Google Scholar
Knutsen, A. L., On kth order embeddings of K3 surfaces and Enriques surfaces , Manuscripta Math. 104 (2001), 211–237.Google Scholar
Knutsen, A. L., Syzdek, W. and Szemberg, T., Moving curves and Seshadri constants , Math. Res. Lett. 16 (2009), 711–719.Google Scholar
Kollár, J., Nonrational hypersurfaces , J. Amer. Math. Soc. 8 (1995), 241–249.CrossRefGoogle Scholar
Kollár, J. and Smith, K., Rational and nearly rational varieties, Cambridge Studies in Advanced Mathematics, vol. 92 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Kuznetsov, A., Derived categories of cubic fourfolds , in Cohomological and geometric approaches to rationality problems, Progress in Mathematics, vol. 282 (Birkhäuser Boston, Boston, MA, 2010), 219–243.CrossRefGoogle Scholar
Lazarsfeld, R., Lengths of periods and Seshadri constants of abelian varieties , Math. Res. Lett. 3 (1996), 439–447.Google Scholar
Lazarsfeld, R., Lectures on linear series , in Complex algebraic geometry, Park City, UT, 1993, IAS/Park City Mathematical Series, vol. 3 (American Mathematical Society, Providence, RI, 1997), 161–219.Google Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry I and II, Ergebnisse der Mathematik und ihrer Grenzgebiete 3. Folge, vols. 48 and 49 (Springer, Berlin, 2004).Google Scholar
Lopez, A. F. and Pirola, G. P., On the curves through a general point on a smooth surface of P 3 , Math. Z. 219 (1995), 93–106.Google Scholar
Mori, S. and Mukai, S., The Uniruledness of the moduli space of curves of genus 11 , in Algebraic geometry (Tokyo/Kyoto, 1982), Lecture Notes in Mathematics, vol. 1016 (Springer, Berlin, 1983), 334–353.CrossRefGoogle Scholar
Mumford, D., Rational equivalence of 0-cycles on surfaces , J. Math. Kyoto Univ. 9 (1969), 195–204.Google Scholar
Pirola, G. P., Curves on generic Kummer varieties , Duke Math. J. 59 (1989), 701–708.Google Scholar
Ran, Z., The (dimension+2)-secant lemma , Invent. Math. 106 (1991), 65–71.Google Scholar
Stapleton, D., The degree of irrationality of very general hypersurfaces in some homogeneous spaces, PhD thesis, Stony Brook University (2017).Google Scholar
Tokunaga, H. and Yoshihara, H., Degree of irrationality of abelian surfaces , J. Algebra 174 (1995), 1111–1121.Google Scholar
Totaro, B., Hypersurfaces that are not stably rational , J. Amer. Math. Soc. 29 (2016), 883–891.Google Scholar
Voisin, C., On a conjecture of Clemens on rational curves on hypersurfaces , J. Differential Geometry 44 (1996), 200–213.CrossRefGoogle Scholar
Voisin, C., Chow rings, decomposition of the diagonal, and the topology of families, Annals of Mathematics Studies, vol. 187 (Princeton University Press, Princeton, NJ, 2014).Google Scholar
Voisin, C., Unirational threefolds with no universal codimension 2 cycle , Invent. Math. 201 (2015), 207–237.CrossRefGoogle Scholar
Yoshihara, H., Degree of irrationality of an algebraic surface , J. Algebra 167 (1994), 634–640.Google Scholar
Yoshihara, H., Degree of irrationality of a product of two elliptic curves , Proc. Amer. Math. Soc. 124 (1996), 1371–1375.Google Scholar
Yoshihara, H., A note on the inequality of degrees of irrationality of algebraic surfaces , J. Algebra 207 (1998), 272–275.Google Scholar
Yoshihara, H., Degree of irrationality of hyperelliptic surfaces , Algebra Colloq. 7 (2000), 319–328.Google Scholar