Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T14:23:24.352Z Has data issue: false hasContentIssue false
  • English
  • Français

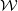$\mathcal {W}$-constraints for the total descendant potential of a simple singularity

Part of: Groups and algebras in quantum theory Symplectic geometry, contact geometry Singularities Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  07 February 2013

Bojko Bakalov  and
Todor Milanov
Bojko Bakalov
Affiliation:
Department of Mathematics, North Carolina State University, Raleigh, NC 27695, USA (email: [email protected])
Todor Milanov
Affiliation:
Kavli IPMU, University of Tokyo (WPI), Kashiwa 277-8583, Japan (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

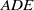Simple, or Kleinian, singularities are classified by Dynkin diagrams of type $ADE$. Let 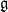$\mathfrak {g}$ be the corresponding finite-dimensional Lie algebra, and 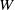$W$ its Weyl group. The set of 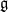$\mathfrak {g}$-invariants in the basic representation of the affine Kac–Moody algebra 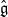$\hat {\mathfrak {g}}$ is known as a $\mathcal {W}$-algebra and is a subalgebra of the Heisenberg vertex algebra 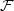$\mathcal {F}$. Using period integrals, we construct an analytic continuation of the twisted representation of 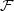$\mathcal {F}$. Our construction yields a global object, which may be called a $W$-twisted representation of 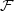$\mathcal {F}$. Our main result is that the total descendant potential of the singularity, introduced by Givental, is a highest-weight vector for the 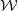$\mathcal {W}$-algebra.

Keywords

Frobenius manifoldsimple singularitytotal descendant potentialvertex algebra$\uppercase {\mathcal {w}}$-algebra

MSC classification

Secondary: 53D45: Gromov-Witten invariants, quantum cohomology, Frobenius manifolds 17B69: Vertex operators; vertex operator algebras and related structures 32S30: Deformations of singularities; vanishing cycles 81R10: Infinite-dimensional groups and algebras motivated by physics, including Virasoro, Kac-Moody, $W$-algebras and other current algebras and their representations
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 5 , May 2013 , pp. 840 - 888
Copyright
Copyright © 2013 The Author(s) 

References

[AvM92]Adler, M. and van Moerbeke, P., A matrix integral solution to two-dimensional $W_p$-gravity, Comm. Math. Phys. 147 (1992), 25–56.CrossRefGoogle Scholar
[Arn75]Arnol’d, V. I., Critical points of smooth functions, and their normal forms, Uspekhi Mat. Nauk 30 (1975), 3–65 (in Russian); English translation, Russian Math. Surveys 30 (1975), 1–75.Google Scholar
[AGV88]Arnol’d, V. I., Gusein-Zade, S. M. and Varchenko, A. N., Singularities of differentiable maps. Vol. II. Monodromy and asymptotics of integrals, Monographs in Mathematics, vol. 83 (Birkhäuser Boston, Inc., Boston, MA, 1988).Google Scholar
[BK04]Bakalov, B. and Kac, V. G., Twisted modules over lattice vertex algebras, in Lie theory and its applications in physics V (World Scientific Publishing, River Edge, NJ, 2004), 3–26, arXiv:math/0402315.Google Scholar
[BK06]Bakalov, B. and Kac, V. G., Generalized vertex algebras, in Lie theory and its applications in physics VI (Heron Press, Sofia, 2006), 3–25, arXiv:math/0602072.Google Scholar
[BM08]Bakalov, B. and Milanov, T., $\mathcal {W}_{N+1}$-constraints for singularities of type $A_N$, Preprint (2008), arXiv:0811.1965.Google Scholar
[BN06]Bakalov, B. and Nikolov, N. M., Jacobi identity for vertex algebras in higher dimensions, J. Math. Phys. 47 (2006), 053505, 30 pp.CrossRefGoogle Scholar
[Beh97]Behrend, K., Gromov–Witten invariants in algebraic geometry, Invent. Math. 127 (1997), 601–617.CrossRefGoogle Scholar
[BD04]Beilinson, A. and Drinfeld, V., Chiral algebras, American Mathematical Society Colloquium Publications, vol. 51 (American Mathematical Society, Providence, RI, 2004).Google Scholar
[BPZ84]Belavin, A. A., Polyakov, A. M. and Zamolodchikov, A. B., Infinite conformal symmetry in two-dimensional quantum field theory, Nuclear Phys. B 241 (1984), 333–380.Google Scholar
[Bor86]Borcherds, R. E., Vertex algebras, Kac–Moody algebras, and the Monster, Proc. Natl. Acad. Sci. USA 83 (1986), 3068–3071.Google Scholar
[Bou02]Bourbaki, N., Lie groups and Lie algebras, in Elements of mathematics (Berlin) (Springer, Berlin, 2002).Google Scholar
[BS95]Bouwknegt, P. and Schoutens, K. (eds), 𝒲-symmetry, Advanced Series in Mathematical Physics, vol. 22 (World Scientific, River Edge, NJ, 1995).Google Scholar
[Bri71]Brieskorn, E., Singular elements of semi-simple algebraic groups, in Proc. ICM, Vol. II (French) (Nice, 1970) (Gauthier-Villars, Paris, 1971), 279–284.Google Scholar
[BPS12a]Buryak, A., Posthuma, H. and Shadrin, S., A polynomial bracket for the Dubrovin–Zhang hierarchies, J. Differential Geom. 92 (2012), 153–185.Google Scholar
[BPS12b]Buryak, A., Posthuma, H. and Shadrin, S., On deformations of quasi-Miura transformations and the Dubrovin–Zhang bracket, J. Geom. Phys. 62 (2012), 1639–1651.Google Scholar
[DK06]De Sole, A. and Kac, V. G., Finite vs affine $W$-algebras, Jpn. J. Math. 1 (2006), 137–261.Google Scholar
[Dic03]Dickey, L. A., Soliton equations and Hamiltonian systems, Advanced Series in Mathematical Physics, vol. 26, second edition (World Scientific, River Edge, NJ, 2003).Google Scholar
[DMS97]Di Francesco, P., Mathieu, P. and Sénéchal, D., Conformal field theory, Graduate Texts in Contemporary Physics (Springer, New York, 1997).CrossRefGoogle Scholar
[DV02]Dijkgraaf, R. and Vafa, C., On geometry and matrix models, Nuclear Phys. B 644 (2002), 21–39.Google Scholar
[DVVV89]Dijkgraaf, R., Vafa, C., Verlinde, E. and Verlinde, H., The operator algebra of orbifold models, Comm. Math. Phys. 123 (1989), 485–526.Google Scholar
[DVV91]Dijkgraaf, R., Verlinde, H. and Verlinde, E., Loop equations and Virasoro constraints in nonperturbative two-dimensional quantum gravity, Nuclear Phys. B 348 (1991), 435–456.Google Scholar
[Don94]Dong, C., Twisted modules for vertex algebras associated with even lattices, J. Algebra 165 (1994), 91–112.Google Scholar
[DL93]Dong, C. and Lepowsky, J., Generalized vertex algebras and relative vertex operators, Progress in Mathematics, vol. 112 (Birkhäuser, Boston, 1993).Google Scholar
[DL96]Dong, C. and Lepowsky, J., The algebraic structure of relative twisted vertex operators, J. Pure Appl. Algebra 110 (1996), 259–295.Google Scholar
[DLM00]Dong, C., Li, H. and Mason, G., Modular-invariance of trace functions in orbifold theory and generalized Moonshine, Comm. Math. Phys. 214 (2000), 1–56.Google Scholar
[Dub96]Dubrovin, B., Geometry of 2D topological field theories, in Integrable systems and quantum groups (Montecatini Terme, 1993), Lecture Notes in Mathematics, vol. 1620 (Springer, Berlin, 1996), 120–348.Google Scholar
[DZ98]Dubrovin, B. and Zhang, Y., Bi-Hamiltonian hierarchies in 2D topological field theory at one-loop approximation, Comm. Math. Phys. 198 (1998), 311–361.Google Scholar
[DZ05]Dubrovin, B. and Zhang, Y., Normal forms of hierarchies of integrable PDEs, Frobenius manifolds and Gromov–Witten invariants, Preprint (2005), new version of arXiv:math/0108160v1.Google Scholar
[DZ99]Dubrovin, B. and Zhang, Y., Frobenius manifolds and Virasoro constraints, Selecta Math. (N.S.) 5 (1999), 423–466.Google Scholar
[Ebe07]Ebeling, W., Functions of several complex variables and their singularities, Graduate Studies in Mathematics, vol. 83 (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar
[EHX97]Eguchi, T., Hori, K. and Xiong, C.-S., Quantum cohomology and Virasoro algebra, Phys. Lett. B 402 (1997), 71–80.CrossRefGoogle Scholar
[EJX98]Eguchi, T., Jinzenji, M. and Xiong, C.-S., Quantum cohomology and free-field representation, Nuclear Phys. B 510 (1998), 608–622.CrossRefGoogle Scholar
[FSZ10]Faber, C., Shadrin, S. and Zvonkine, D., Tautological relations and the $r$-spin Witten conjecture, Ann. Sci. Éc. Norm. Supér. (4) 43 (2010), 621–658.CrossRefGoogle Scholar
[FJR08]Fan, H., Jarvis, T. and Ruan, Y., Geometry and analysis of spin equations, Comm. Pure Appl. Math. 61 (2008), 745–788.CrossRefGoogle Scholar
[FL88]Fateev, V. A. and Lukyanov, S. L., The models of two-dimensional conformal quantum field theory with $Z_n$ symmetry, Internat. J. Modern Phys. A 3 (1988), 507–520.Google Scholar
[FF90]Feigin, B. and Frenkel, E., Quantization of the Drinfeld–Sokolov reduction, Phys. Lett. B 246 (1990), 75–81.Google Scholar
[FF96]Feigin, B. and Frenkel, E., Integrals of motion and quantum groups, in Integrable systems and quantum groups (Montecatini Terme, 1993), Lecture Notes in Mathematics, vol. 1620 (Springer, Berlin, 1996), 349–418.Google Scholar
[FFR91]Feingold, A. J., Frenkel, I. B. and Ries, J. F. X., Spinor construction of vertex operator algebras, triality, and E (1)8, Contemporary Mathematics, vol. 121 (American Mathematical Society, Providence, RI, 1991).CrossRefGoogle Scholar
[Fre85]Frenkel, I. B., Representations of Kac–Moody algebras and dual resonance models, in Applications of group theory in physics and mathematical physics (Chicago, 1982), Lectures in Applied Mathematics, vol. 21 (American Mathematical Society, Providence, RI, 1985), 325–353.Google Scholar
[FB01]Frenkel, E. and Ben-Zvi, D., Vertex algebras and algebraic curves, Mathematical Surveys and Monographs, vol. 88, second edition (American Mathematical Society, Providence, RI, 2001).Google Scholar
[FGM10]Frenkel, E., Givental, A. and Milanov, T., Soliton equations, vertex operators, and simple singularities, Funct. Anal. Other Math. 3 (2010), 47–63.Google Scholar
[FK80]Frenkel, I. B. and Kac, V. G., Basic representations of affine Lie algebras and dual resonance models, Invent. Math. 62 (1980), 23–66.CrossRefGoogle Scholar
[FKRW95]Frenkel, E., Kac, V., Radul, A. and Wang, W., $\mathcal {W}_{1+\infty }$ and $\mathcal {W}(\mathfrak {gl}_N)$ with central charge $N$, Comm. Math. Phys. 170 (1995), 337–357.CrossRefGoogle Scholar
[FKW92]Frenkel, E., Kac, V. and Wakimoto, M., Characters and fusion rules for $W$-algebras via quantized Drinfeld–Sokolov reduction, Comm. Math. Phys. 147 (1992), 295–328.Google Scholar
[FLM87]Frenkel, I. B., Lepowsky, J. and Meurman, A., Vertex operator calculus, in Mathematical aspects of string theory, Advanced Series in Mathematical Physics, vol. 1 (World Scientific Publishing, Singapore, 1987), 150–188.CrossRefGoogle Scholar
[FLM88]Frenkel, I. B., Lepowsky, J. and Meurman, A., Vertex operator algebras and the Monster, Pure and Applied Mathematics, vol. 134 (Academic Press, Boston, 1988).Google Scholar
[FS04]Frenkel, E. and Szczesny, M., Twisted modules over vertex algebras on algebraic curves, Adv. Math. 187 (2004), 195–227.Google Scholar
[FZ92]Frenkel, I. B. and Zhu, Y., Vertex operator algebras associated to representations of affine and Virasoro algebras, Duke Math. J. 66 (1992), 123–168.Google Scholar
[FKN91]Fukuma, M., Kawai, H. and Nakayama, R., Continuum Schwinger–Dyson equations and universal structures in two-dimensional quantum gravity, Internat. J. Modern Phys. A 6 (1991), 1385–1406.CrossRefGoogle Scholar
[Get02]Getzler, E., A Darboux theorem for Hamiltonian operators in the formal calculus of variations, Duke Math. J. 111 (2002), 535–560.Google Scholar
[Giv01a]Givental, A., Semisimple Frobenius structures at higher genus, Int. Math. Res. Not. (2001), 1265–1286.Google Scholar
[Giv01b]Givental, A., Gromov–Witten invariants and quantization of quadratic Hamiltonians, Mosc. Math. J. 1 (2001), 551–568.CrossRefGoogle Scholar
[Giv03]Givental, A., $A_{n-1}$ singularities and $n$KdV Hierarchies, Mosc. Math. J. 3 (2003), 475–505.CrossRefGoogle Scholar
[GM05]Givental, A. and Milanov, T., Simple singularities and integrable hierarchies, in The breadth of symplectic and Poisson geometry, Progress in Mathematics, vol. 232 (Birkhäuser Boston, Boston, MA, 2005), 173–201.Google Scholar
[God89]Goddard, P., Meromorphic conformal field theory, in Infinite-dimensional Lie algebras and groups (Luminy–Marseille, 1988), Advanced Series in Mathematical Physics, vol. 7 (World Scientific Publishing, Teaneck, NJ, 1989), 556–587.Google Scholar
[Goe91]Goeree, J., $W$-constraints in $2D$ quantum gravity, Nuclear Phys. B 358 (1991), 737–757.Google Scholar
[Her02]Hertling, C., Frobenius manifolds and moduli spaces for singularities, Cambridge Tracts in Mathematics, vol. 151 (Cambridge University Press, Cambridge, 2002).Google Scholar
[JKV01]Jarvis, T., Kimura, T. and Vaintrob, A., Moduli spaces of higher spin curves and integrable hierarchies, Compositio Math. 126 (2001), 157–212.Google Scholar
[Kac90]Kac, V. G., Infinite-dimensional Lie algebras, third edition (Cambridge University Press, Cambridge, 1990).Google Scholar
[Kac96]Kac, V. G., Vertex algebras for beginners, University Lecture Series, vol. 10, second edition (American Mathematical Society, Providence, RI, 1996).Google Scholar
[KKLW81]Kac, V. G., Kazhdan, D. A., Lepowsky, J. and Wilson, R. L., Realization of the basic representations of the Euclidean Lie algebras, Adv. Math. 42 (1981), 83–112.Google Scholar
[KP85]Kac, V. G. and Peterson, D. H., $112$ constructions of the basic representation of the loop group of $E_8$, in Symposium on anomalies, geometry, topology (Chicago, IL, 1985) (World Scientific Publishing, Singapore, 1985), 276–298.Google Scholar
[KS91]Kac, V. and Schwarz, A., Geometric interpretation of the partition function of 2D gravity, Phys. Lett. B 257 (1991), 329–334.Google Scholar
[KT97]Kac, V. G. and Todorov, I. T., Affine orbifolds and rational conformal field theory extensions of $W_{1+\infty }$, Comm. Math. Phys. 190 (1997), 57–111.Google Scholar
[KW89]Kac, V. G. and Wakimoto, M., Exceptional hierarchies of soliton equations, in Theta functions—Bowdoin 1987 (Brunswick, ME, 1987), Proceedings of Symposia in Pure Mathematics, vol. 49, part 1 (American Mathematical Society, Providence, RI, 1989), 191–237.Google Scholar
[KWY98]Kac, V. G., Wang, W. and Yan, C. H., Quasifinite representations of classical Lie subalgebras of $\mathcal {W}_{1+\infty }$, Adv. Math. 139 (1998), 56–140.Google Scholar
[KMMMP93]Kharchev, S., Marshakov, A., Mironov, A., Morozov, A. and Pakuliak, S., Conformal matrix models as an alternative to conventional multi-matrix models, Nuclear Phys. B 404 (1993), 717–750.Google Scholar
[Kon92]Kontsevich, M., Intersection theory on the moduli space of curves and the matrix Airy function, Comm. Math. Phys. 147 (1992), 1–23.Google Scholar
[Kon95]Kontsevich, M., Enumeration of rational curves via toric actions, in The moduli space of curves, Progress in Mathematics, vol. 129 (Birkhäuser Boston, Boston, MA, 1995), 335–368.CrossRefGoogle Scholar
[KM94]Kontsevich, M. and Manin, Yu., Gromov–Witten classes, quantum cohomology, and enumerative geometry, Comm. Math. Phys. 164 (1994), 525–562.Google Scholar
[Kos92]Kostov, I. K., Gauge invariant matrix model for the $\hat A-\hat D-\hat E$ closed strings, Phys. Lett. B 297 (1992), 74–81.Google Scholar
[Lep85]Lepowsky, J., Calculus of twisted vertex operators, Proc. Natl. Acad. Sci. USA 82 (1985), 8295–8299.Google Scholar
[Lep88]Lepowsky, J., Perspectives on vertex operators and the Monster, in The mathematical heritage of Hermann Weyl, Proceedings of Symposia in Pure Mathematics, vol. 48 (American Mathematical Society, Providence, RI, 1988), 181–197.Google Scholar
[LL04]Lepowsky, J. and Li, H., Introduction to vertex operator algebras and their representations, Progress in Mathematics, vol. 227 (Birkhäuser Boston, Boston, MA, 2004).Google Scholar
[LW78]Lepowsky, J. and Wilson, R. L., Construction of the affine Lie algebra $A_1^{(1)}$, Comm. Math. Phys. 62 (1978), 43–53.Google Scholar
[Li96]Li, H., Local systems of twisted vertex operators, vertex operator superalgebras and twisted modules, in Moonshine, the Monster, and related topics, Contemporary Mathematics, vol. 193 (American Mathematical Society, Providence, RI, 1996), 203–236.CrossRefGoogle Scholar
[LT98]Li, J. and Tian, G., Virtual moduli cycles and Gromov–Witten invariants in general symplectic manifolds, in Topics in symplectic 4-manifolds (Irvine, CA, 1996), First Int. Press Lect. Ser. I (Internat. Press, Cambridge, MA, 1998), 47–83.Google Scholar
[Loo75]Looijenga, E., A period mapping for certain semi-universal deformations, Compositio Math. 30 (1975), 299–316.Google Scholar
[MSV99]Malikov, F., Schechtman, V. and Vaintrob, A., Chiral de Rham complex, Comm. Math. Phys. 204 (1999), 439–473.Google Scholar
[Man99]Manin, Yu. I., Frobenius manifolds, quantum cohomology, and moduli spaces, American Mathematical Society Colloquium Publications, vol. 47 (American Mathematical Society, Providence, RI, 1999).Google Scholar
[Mil06]Milanov, T., Gromov–Witten theory of $\mathbb {C}P^1$and integrable hierarchies, Preprint (2006), arXiv:math-ph/0605001.Google Scholar
[Mil08]Milanov, T., The equivariant Gromov–Witten theory of $\mathbb {C}\mathrm {P}^1$ and integrable hierarchies, Int. Math. Res. Not. 2008 (2008), doi:10.1093/imrp/rnn073.Google Scholar
[MT08]Milanov, T. and Tseng, H.-H., The spaces of Laurent polynomials, Gromov–Witten theory of $\mathbb {P}^1$-orbifolds, and integrable hierarchies, J. Reine Angew. Math. 622 (2008), 189–235.Google Scholar
[MT11]Milanov, T. and Tseng, H.-H., Equivariant orbifold structures on the projective line and integrable hierarchies, Adv. Math. 226 (2011), 641–672.CrossRefGoogle Scholar
[OP06]Okounkov, A. and Pandharipande, R., The equivariant Gromov–Witten theory of ℙ1, Ann. of Math. (2) 163 (2006), 561–605.Google Scholar
[Ros10]Rossi, P., Gromov–Witten theory of orbicurves, the space of tri-polynomials and symplectic field theory of Seifert fibrations, Math. Ann. 348 (2010), 265–287.Google Scholar
[RT95]Ruan, Y. and Tian, G., A mathematical theory of quantum cohomology, J. Differential Geom. 42 (1995), 259–367.Google Scholar
[Sai82]Saito, K., On periods of primitive integrals, I, Preprint, RIMS (1982).Google Scholar
[Sai85]Saito, K., Extended affine root systems I. Coxeter transformations, Publ. Res. Inst. Math. Sci., Kyoto Univ. 21 (1985), 75–179.Google Scholar
[Sai89]Saito, M., On the structure of Brieskorn lattice, Ann. Inst. Fourier 39 (1989), 27–72.Google Scholar
[ST08]Saito, K. and Takahashi, A., From primitive forms to Frobenius manifolds. From Hodge theory to integrability and TQFT $tt^*$-geometry, Proc. Sympos. Pure Math. 78 (2008), 31–48.Google Scholar
[Seg81]Segal, G., Unitary representations of some infinite-dimensional groups, Comm. Math. Phys. 80 (1981), 301–342.Google Scholar
[Slo80]Slodowy, P., Simple singularities and simple algebraic groups, Lecture Notes in Mathematics, vol. 815 (Springer, Berlin, 1980).Google Scholar
[Tel12]Teleman, C., The structure of 2D semi-simple field theories, Invent. Math. 188 (2012), 525–588.Google Scholar
[vdL96]van de Leur, J., The $n$th reduced BKP hierarchy, the string equation and $BW_{1+\infty }$-constraints, Acta Appl. Math. 44 (1996), 185–206.Google Scholar
[vM94]van Moerbeke, P., Integrable foundations of string theory, in Lectures on integrable systems (Sophia-Antipolis, 1991) (World Scientific Publishing, River Edge, NJ, 1994), 163–267.Google Scholar
[Wit91]Witten, E., Two-dimensional gravity and intersection theory on moduli space, in Surveys in differential geometry (Lehigh Univ, Bethlehem, PA, 1991), 243–310.Google Scholar
[Wit92]Witten, E., On the Kontsevich model and other models of two-dimensional gravity, in Proc. XXth int. conf. on differential geometric methods in theoretical physics, vols 1, 2 (New York, 1991) (World Scientific Publishing, River Edge, NJ, 1992), 176–216.Google Scholar
[Wit93]Witten, E., Algebraic geometry associated with matrix models of two-dimensional gravity, in Topological models in modern mathematics (Publish or Perish, Houston, TX, 1993), 235–269.Google Scholar
[Zam85]Zamolodchikov, A. B., Infinite extra symmetries in two-dimensional conformal quantum field theory, Teoret. Mat. Fiz. 65 (1985), 347–359 (in Russian); English translation, Theoret. and Math. Phys. 65 (1985), 1205–1213.Google Scholar