Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-21T09:20:47.008Z Has data issue: false hasContentIssue false
  • English
  • Français

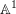$\mathbb{A}^{1}$-homotopy invariants of topological Fukaya categories of surfaces

Part of: Homological algebra

Published online by Cambridge University Press:  09 June 2017

Tobias Dyckerhoff
Tobias Dyckerhoff*
Affiliation:
Hausdorff Center for Mathematics, Endenicher Allee 62, 53115 Bonn, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide an explicit formula for localizing 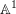$\mathbb{A}^{1}$-homotopy invariants of topological Fukaya categories of marked surfaces. Following a proposal of Kontsevich, this differential 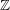$\mathbb{Z}$-graded category is defined as global sections of a constructible cosheaf of dg categories on any spine of the surface. Our theorem utilizes this sheaf-theoretic description to reduce the calculation of invariants to the local case when the surface is a boundary-marked disk. At the heart of the proof lies a theory of localization for topological Fukaya categories which is a combinatorial analog of Thomason–Trobaugh’s theory of localization in the context of algebraic 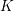$K$-theory for schemes.

Keywords

topological Fukaya categories∞-categoriesSegal spacesK-theory

MSC classification

Primary: 18G55: Homotopical algebra
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 8 , August 2017 , pp. 1673 - 1705
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beilinson, A., Coherent sheaves on Pn and problems of linear algebra , Funct. Anal. Appl. 12 (1978), 214–216.CrossRefGoogle Scholar
Blanc, A., Topological K-theory of complex noncommutative spaces , Compositio Math. 152 (2016), 489–555.CrossRefGoogle Scholar
Bocklandt, R., Noncommutative mirror symmetry for punctured surfaces, Preprint (2011),arXiv:1111.3392.Google Scholar
Dyckerhoff, T. and Kapranov, M., Higher Segal spaces I, Preprint (2012), arXiv:1212.3563.Google Scholar
Dyckerhoff, T. and Kapranov, M., Triangulated surfaces in triangulated categories, e-Print (2013), arXiv:1306.2545.Google Scholar
Dyckerhoff, T. and Kapranov, M., Crossed simplicial groups and structured surfaces , in Stacks and categories in geometry, topology, and algebra, Contemporary Mathematics, vol. 643 (American Mathematical Society, Providence, RI, 2015), 37–110, doi:10.1090/conm/643/12896.CrossRefGoogle Scholar
Fiedorowicz, Z. and Loday, J.-L., Crossed simplicial groups and their associated homology , Trans. Amer. Math. Soc. 326 (1991), 57–87.CrossRefGoogle Scholar
Haiden, F., Katzarkov, L. and Kontsevich, M., Stability in Fukaya categories of surfaces, Preprint (2014), arXiv:1409.8611.Google Scholar
Keller, B., Invariance and localization for cyclic homology of DG algebras , J. Pure Appl. Algebra 123 (1998), 223–273.CrossRefGoogle Scholar
Kontsevich, M., Symplectic geometry of homological algebra, available at the author’s webpage (2009), http://www.ihes.fr/∼maxim/TEXTS/Symplectic_AT2009.pdf.Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009).CrossRefGoogle Scholar
Lurie, J., Higher algebra, Preprint (2011),http://www.math.harvard.edu/∼lurie/papers/HA.pdf.Google Scholar
Lurie, J., Rotation invariance in algebraic K-theory, Preprint (2014),http://www.math.harvard.edu/∼lurie/papers/Waldhaus.pdf.Google Scholar
Nadler, D., Arboreal singularities, Preprint (2013), arXiv:1309.4122.Google Scholar
Nadler, D., Fukaya categories as categorical morse homology , SIGMA Symmetry Integrability Geom. Methods Appl. 10 (2014), 18–47.Google Scholar
Nadler, D., Cyclic symmetries of An -quiver representations , Adv. Math. 269 (2015), 346–363.CrossRefGoogle Scholar
Pascaleff, J. and Sibilla, N., Topological Fukaya category and mirror symmetry for punctured surfaces, Preprint (2016), arXiv:1604.06448.Google Scholar
Rezk, C., A model for the homotopy theory of homotopy theory , Trans. Amer. Math. Soc. 353 (2001), 973–1007 (electronic).CrossRefGoogle Scholar
Segal, G., Categories and cohomology theories , Topology 13 (1974), 293–312.CrossRefGoogle Scholar
Seidel, P., Exact Lagrangian submanifolds in T ∗ S n and the graded Kronecker quiver , in Different faces of geometry, International Mathematical Series (New York), vol. 3 (Kluwer/Plenum, New York, 2004), 349–364; MR 2103000 (2005h:53153).CrossRefGoogle Scholar
Sibilla, N., Treumann, D. and Zaslow, E., Ribbon graphs and mirror symmetry , Selecta Math. (N.S.) 20 (2014), 979–1002.CrossRefGoogle Scholar
Tabuada, G., Une structure de catégorie de modèles de Quillen sur la catégorie des dg-catégories , C. R. Math. Acad. Sci. Paris 340 (2005), 15–19.CrossRefGoogle Scholar
Tabuada, G., The fundamental theorem via derived Morita invariance, localization, and A1 -homotopy invariance , J. K-Theory 9 (2012), 407–420, doi:10.1017/is011004009jkt155.CrossRefGoogle Scholar
Toën, B., The homotopy theory of dg-categories and derived Morita theory , Invent. Math. 167 (2007), 615–667.CrossRefGoogle Scholar
Thomason, R. W. and Trobaugh, T., Higher algebraic K-theory of schemes and of derived categories , in The Grothendieck Festschrift, Vol. III, Progress in Mathematics, vol. 88 (Birkhäuser Boston, Boston, MA, 1990), 247–435; MR 1106918 (92f:19001).CrossRefGoogle Scholar
Toën, B. and Vaquié, M., Moduli of objects in dg-categories , Ann. Sci. Éc. Norm. Supér. (4) 40 (2007), 387–444, doi:10.1016/j.ansens.2007.05.001.CrossRefGoogle Scholar
Tabuada, G. and Van den Bergh, M., The Gysin triangle via localization and A1-homotopy invariance, Preprint (2015), arXiv:1510.04677.Google Scholar